1. Материальная точка - тело, размерами которого в данных условиях движения можно пренебречь.

Абсолютно твердым телом называется тело, деформациями которого по условиям задачи можно пренебречь. У абсолютно твердого тела расстояние между любыми его точками с течением времени не меняется. В термодинамическом смысле такое тело не обязательно должно быть твердым. Произвольное движение твердого тела может быть разбито на поступательное и вращательное вокруг неподвижной точки. Сила (ньютонова) – мера механического воздействия на некото- рое материальное тело со стороны другого материального тела (или физического поля); она характеризует интенсивность и направление этого воздействия. Это, разумеется, не определение, а лишь пояснение к понятию силы. Поскольку понятие силы – фундаментальное, то его точный смысл раскрывается в аксиомах механики.

Равнодействующая - это просто сумма (векторная) всех сил, действующих на тело. Скажем, кирпич скользит по наклонной доске: на него действует вес, сила трения и сила реакции опоры, и из этих трёх получается одна равнодействующая. По определению, равнодействующей называется ОДНА сила, действие которой идентично суммарному действию всех других сил, действующих на тело. А уравновешивающая - она уравновешивающая и есть. Она всегда действует в паре с ОДНОЙ какой-то силой, всегда равна ей по величине и противоположна по направлению. Чтоб уравновесить. То есть это такая сила, для которой результат её действия И действия какой-то ещё силы (которую она уравновешивает) эквивалентен отсутствию сил вообще.

2.

Аксиомы статики

Понятие и особенности твердого тела, равновесия, силы. Содержание аксиом статики, выведенных в результате обобщений многочисленных опытов и наблюдений за равновесием и движением тел. Изучение направления реакции связи, препятствующей перемещению тела.

3. Связи и их реакции

    Тела в природе бывают свободными и несвободными. Тела, свобода перемещения которых ничем не ограничена, называются свободными. Тела, ограничивающие свободу перемещения других тел, называются по отношению к ним связями. 

    Одним из основных положений механики является принцип освобождаемости от связей, согласно которому несвободное тело можно рассматривать как свободное, если отбросить действующие на него связи и заменить их силами – реакциями связей.

4. Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.

Теорема

Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.

5.     Проекция силы на ось – это алгебраическая величина, равная произведению модуля силы на косинус угла между положительным направлением оси и вектором силы (т.е. это отрезок, откладываемый силой на соответствующие оси. Рисунок 1.13):

 F_x= Fcosα;

P_x= Pcosβ= P⋅ cos90^o=0;

R_x= Rcosγ = -R⋅ cos(180^o-γ).   

6. Две параллельные силы, равные по величине и направленные в противоположные стороны, называются парой сил (фиг.30, а). Расстояние d между линиями действия сил пары называется плечом пары. Пару сил нельзя заменить и уравновесить одной силой. Уравновесить пару сил можно только другой парой. Пара сил, при­ложенная к твердому телу, вызывает его вращение, характеризую­щееся моментом пары. Моментом пары сил называется взятое со знаком (+) или (-) произведение величины одной из сил на ее плечо:m = ±Pd. Момент пары считается положительным, если пара стремится вращать тело против вращения часовой стрелки. Пару сил принято изображать изогнутой стрелкой (фиг.30, б). Буква у конца стрелки обозначает момент пары.

Условие равновесия пар: для равновесия нескольких пар необхо­димо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю.

7.

Если под действием приложенной силы твердое тело может совершать вращение вокруг некоторой точки, то для того, чтобы охарактеризовать вращательный эффект силы вводится понятие – момент силы относительно точки (или центра).

Моментом силы относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора  точки  приложения силы на вектор силы. 

                                                M_o(F) = r ⊗ F

8. Плоской системой произвольно расположенных силназывается система сил, линии, действия которых лежат в одной плоскости, но не пересекаются в одной точке (рис. 1.21). Для того чтобы привести данную систему произвольно расположенных сил к произвольно выбранной точке О (см. рис. 1.21), необходимо:

1) перенести по очереди каждую силу в эту точку;

2) уравновесить силы (F₁^', F₂^’, F₃^’) силами. (F₁^'’, F₂^’’, F₃^’’)

В результате приведения сил (F₁, F₂, F₃) к точке О получили новую сис­тему сил, состоящую из плоской системы сходящихся сил (F₁,F₂,F₃), кото­рые равны и параллельны данным силам, т.е.

F₁^'= F₁ , F₂,= F₂^’, F₃^' = F₃ . (1.1)

Эту вновь полученную систему сходящихся сил (1.1) заменяем равнодей­ствующей силой, которая равна геометрической сумме данных сил и назы­вается главным вектором системы:

 

Врезультате приведения получили еще одну систему пар сил

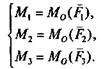
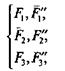
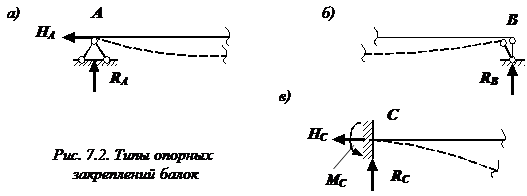
9.Существуют виды опор балок (рис. 7.2):

шарнирно неподвижная опора;

шарнирно подвижная опора;

жесткая заделка.

Шарнирно неподвижная опора

Шарнирно неподвижная опора (рис. 7.2, а, опора А) - это закрепление конца балки, при которомбалка может поворачиваться, но не может перемещаться ни в горизонтальном (влево или вправо), ни в вертикальном (вверх или вниз) направлениях, то есть не может перемещаться ни в каком направлении. В шарнирно неподвижной опоре может возникнуть реакция, которую удобно представить в виде двух составляющих: вертикальной ( ) и горизонтальной ( ).

Шарнирно неподвижная опора на расчетной схеме условно изображается посредством двух стерженьков. Нижние их концы шарнирно прикреплены к «земле», а верхние концы соединены между собой и с балкой шарниром.