Зміст

Вступ 4

1. Динамічний синтез важільного механізму за коефіцієнтом нерівномірності руху. 5

2. Динамічний аналіз важільного механізму. 12

3. Проектування кінематичної схеми планетарного редуктора та побудова картини евольвентного зачеплення. 14

3.1 Проектування кінематичної схеми планетарного редуктора. 14

3.2 Побудова картини евольвентного зачеплення. 15

4. Синтез кулачкового механізму. 16

Література 17

Вступ

Тео́рія маши́н і механі́змів (ТММ) — це наукова дисципліна про загальні методи дослідження будови, кінематики і динаміки механізмів і машин та про наукові основи їх проектування. Курс ТММ як навчальна дисципліна базується на знаннях в галузях математики, фізики, теоретичної механіки, інженерної графіки та ін. Він є, у свою чергу, базою для вивчення та розвитку таких дисциплін, як деталі машин, підйомно-транспортні машини, металорізальні верстати та ін.

Як самостійна наукова дисципліна ТММ, подібно до інших прикладних розділів механіки, виникла в результаті промислової революції початок якої відноситься до 30-х років XVIII століття, хоча машини створювались задовго до цього і найпростіші механізми (важіль, колесо, гвинтова передача та ін.) широко використовувались уже в Стародавньому Єгипті та інших цивілізаціях античної доби.

Весь попередній період розвитку техніки можна розглядати як період емпіричного створення машин, протягом якого робляться винаходи та створюються конструкції великої кількості машин і механізмів, серед яких: підйомники, вітряні та водяні млини, помпи, каменедробарки, ткацькі і токарні верстати, парові машини (винахідники: Леонардо да Вінчі, Е.Картрайт, Дж. Кей, Дж. Стефенсон, Дж. Ватт та ін.).

Теорія механізмів і машин як наука почала формуватись на початку XIX сторіччя. У цей період закладаються основи майбутньої теорії. Формулюються основні закони механіки: закони збереження енергії та імпульсу, «золоте правило механіки», закони тертя. Розвиваються поняття про передавальне відношення, основи геометричної теорії евольвентного зачеплення, пропонуються вирішення низки задач з кінематики і динаміки твердого тіла (вчені: Л. Карно, Ш.Кулон, Г. Амонтон, Дж. Кардано, Л. Ейлер).

1. Динамічний синтез важільного механізму за коефіцієнтом нерівномірності руху.

Для заданого механізму проводимо структурний аналіз. Для цього з’ясовуємо та записуємо, які кінематичні пари утворюють ланки міх собою (обертальні, поступальні чи вищі) та вказуємо їх клас. Після цього шукаємо ступінь рухомості механізму.

Ступінь рухомості плоского механізму (рух ланок якого здійснюється в одній або паралельних площинах) та кількість ведучих ланок визначаємо за формулою Чебишева:

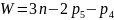(1,1)

де n – кількість рухомих ланок; p4 і p5 відповідно кількість кінематичних пар ІV і V класів.

Далі виділяємо структурні групи, які входять до складу механізму та ведучу ланку, наводимо їх рисунки у пояснювальній записці (рис. 1.1).

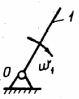
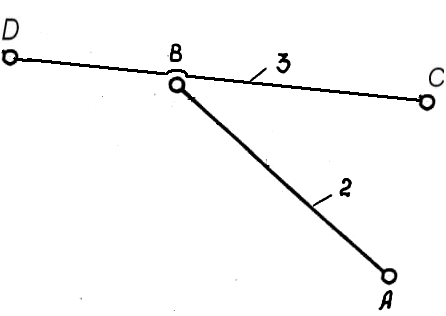
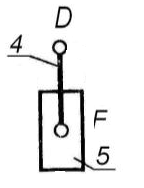
Рис. 1.1. Приклад виділення структурних груп

Склад механізму і послідовність приєднання до ведучої ланки структурних груп виражаємо формулою будови механізму. У цій формулі римськими цифрами позначаємо класи ведучої ланки і структурних груп, а в круглих дужках арабськими цифрами – номери ланок, які входять до їх складу. Так, наприклад, формула будови може мати вигляд:

I(0;1) I(2;3) II(4;5) (1,2)

Вона вказує на те, що до механізму першого класу (ведучої ланки), який утворений стояком 0 і кривошипом 1 і механізмом першого класу, який утворений відповідно ланками 2, 3 послідовно приєднано одну структурну групу другого класу, яка утворена відповідно ланками 4, 5. З формули будови можна зробити висновок, що даний механізм є механізмом другого класу.

Динамічний синтез механізму за коефіцієнтом нерівномірності руху полягає у визначенні моменту інерції маховика, який забезпечить рух ланки зведення із заданою нерівномірністю. Синтез ведуть у такій послідовності.

1. У лівій частині креслення будуємо плани положень механізму для 12 рівновіддалених положень ведучої ланки (кривошипа ОА). За початкове (нульове) положення кривошипа вибираємо таке його положення, при якому ведена ланка займає одне із крайніх положень (у цьому положенні швидкість характерної точки, яка належить веденій ланці, рівна нулю).

Побудову положень ланок плоских механізмів можна здійснити методами засічок, кругових шаблонів і геометричних місць.

Побудову здійснюємо у певному масштабі. Для цього використовуємо масштабний коефіцієнт, під яким розуміємо відношення фізичної величини (шляху, швидкості тощо) до довжини відрізка, який цю величину зображає на рисунку. Масштабний коефіцієнт, який ще називають "масштабом", позначають літерою μ з індексом тієї величини, яка зображена графічно. Наприклад, при зображенні лінійних розмірів механізму масштаб буде визначатися за формулою:

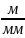, (1,3)

де lOA – дійсна величина кривошипа ОА, м;

ОА – довжина відрізка ОА, мм.

;

;

;

;

.

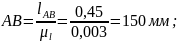
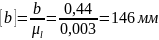2. Будуємо у довільному масштабі 12 повернутих планів швидкостей. Для зручності приймаємо довжину вектора, який зображає швидкість точки А кривошипа.

Масштабний коефіцієнт швидкостей визначають за формулою :

(1,4)

де VA – швидкість точки А, м/с.;

ра – довжина відрізка, що зображає цю швидкість на кресленні, мм.

3. Будуємо графік зведеного моменту інерції від кута повороту кривошипа. За ланку зведення вибираємо кривошип механізму.

Для кожного положення механізму зведений момент інерції ланок визначаємо за формулою:

(1,5)

де mi – маса і-тої ланки; Jsi - момент інерції і-тої ланки відносно осі, яка проходить через центр мас ланки; ωі- кутова швидкість і-тої ланки; Vsi - швидкість центра мас і-тої ланки; ω1 - кутова швидкість обертання кривошипа.

Розраховуюємо рушійну силу, яка діє на поршень в інших положеннях.

Будуючи діаграму, слід враховувати знак рушійної сили. При циклі розширення Fр додатня, а при всіх інших циклах - від'ємна, бо діє проти руху поршня.

Для технологічних машин силу корисного опору, яка діє на ведену ланку, визначаємо у відповідності з графіком зміни сили корисного опору від переміщення веденої ланки у заданому положенні кривошипа (рис. 1,1).

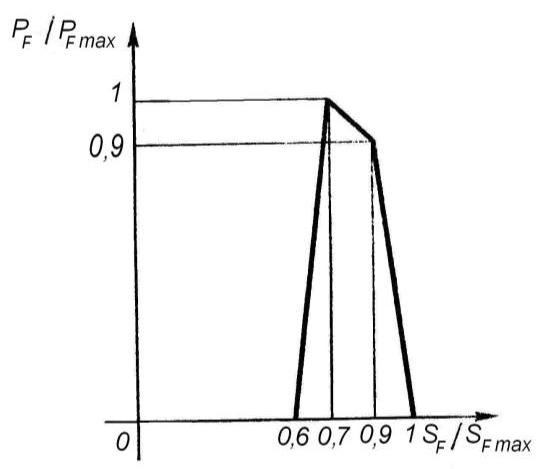
Рис.1.2 Індикаторна діаграма

Спочатку, користуючись планами положень механізму, для заданого положення кривошипа підраховуємо значення відношення SF/ SFmах, де SF – переміщення веденої ланки (у даному випадку т. F) в положенні, для якого здійснюється розрахунок; SFmах – хід веденої ланки. За числовим 32 значенням відношення SF/ SFmах визначаємо величину сили корисного опору для заданого положення кривошипу:

РF=РFmахSF/SFmах (1,6)

Для механізмів компресорів та насосів величину сили корисного опору визначаємо за діаграмами залежності зміни тиску в їх циліндрах від переміщення поршня у положенні кривошипа, для якого здійснюється розрахунок. Послідовність розрахунків така ж, як і для ДВЗ.

5. Зведений момент (від рушійних сил для ДВЗ і сил опору для технологічних машин) для 12 положень механізму визначаємо методом Жуковського, для цього зведений момент подаємо у вигляді пари сил з плечем LО1А:

Мзв=Рзв LО1А (1,7)

де Рзв – складова пари сил, яку називають зведеною силою.

Вважаємо, що зведена сила Рзв прикладена у точці А перпендикулярно до кривошипа. Її величину знаходимо з умови рівності моменту зведеної сили відносно полюса повернутого на 90° плану швидкостей (важеля Жуковського) та суми моментів відносно цього ж полюса від рушійних сил і сил ваги ланок для ДВЗ або сил корисного опору і сил ваги для технологічних машин.

6. Графік роботи сил опору і рушійних сил будуємо методом графічного інтегрування у відповідності з діаграмами МО(φ) та МР(φ). Побудову ведуть у масштабі:

(1,8)

де Н – полюсна віддаль на діаграмі, мм.

7. Зведений момент від рушійних сил і зведений момент від сил опору визначаємо з умови рівності роботи цих моментів відповідно роботі зведених сил опору і роботі рушійних сил за один цикл руху:

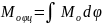(1,9)

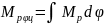(1,10)

тобто з умови рівності площ під кривими МО(φ) та МР(φ).

Для цього на графіку А=А(φ) з'єднуємо початок і кінець кривої АО(φ) або АР(φ) прямою лінією. Диференціюючи графічно цю пряму на графіку А=А(φ) будуємо відповідно графік МР(φ) моменту рушійних сил для технологічних машин або сил опору МО(φ) для двигунів.

8. Будуємо діаграму приросту кінетичної енергії

(1,11)

Для цього в системі координат вверх або вниз від осі абсцис відкладаємо різницю ординат графіків АР(φ) та АО(φ).

9. Діаграму енергія-маса будуємо шляхом графічного виключення параметра φ ( кута повороту кривошипа), з графіків зміни кінетичної енергії механізму і зведеного моменту інерції Jзв(φ).

10. Визначаємо момент інерції маховика за заданим коефіцієнтом нерівномірності руху проводимо дотичні до графіка енергія-маса під кутами до осі абсцис, тангенси, які обчислюються за формулами:

(1,12)

(1,13)

де ω1 – задана середня кутова швидкість обертання кривошипа.

Момент інерції маховика, потрібний для забезпечення заданого коефіцієнта нерівномірності ходу δ, визначаємо за формулою:

(1,14)

де kl – відрізок, який відтинає дотичні на осі ординат діаграми енергія-маса, в мм.

11. Визначаємо масу і габаритні розміри маховика. Конструктивно маховик виготовляють у вигляді дисків або кілець зі спицями. Маса обода маховика зі спицями

(1,15)

Маса маховика зі спицями та маточиною

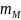
(1,16)

де D – середній діаметр обода маховика в м.; ζ=(1,1-1,3) – коефіцієнт, який враховує масу маточини і спиць маховика.

Середній діаметр D обода маховика приймають конструктивно в 2-4 рази більшим від радіуса. Поперечний переріз обода маховика приймаємо у вигляді прямокутника, в якому

В (1,17)

де B – ширина прямокутника в м; h – висота прямокутника в м. Висота обода маховика у такому випадку

(1,18)

де ρ – густина матеріалу маховика в кг/м³. Для сірого чавуну ρ=7100 кг/м³, а для сталі ρ=7800 кг/м³.