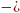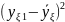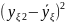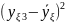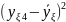3. Проведение математического моделирования технологического процесса

3.1. Обоснование необходимости проведения моделирования технологического процесса.

Современный технологический процесс характеризуется повышенной сложностью и наличием множества контролируемых и неконтролируемых факторов, влияющих на него.

Поэтому мы не можем учитывать все факторы, влияющие на процесс, так как это займет очень много времени и это в большинстве случаев не нужно, так как сколь-нибудь значимое влияние на выходной фактор, обычно, оказывают 2-3 входящих фактора. Следовательно экономически и исходя из затраты времени целесообразно рассматривать только их и на их основе создавать математическую модель. Как правило, математическая модель является при этом верной, следовательно, после того как мы учли или устранили данные факторы, на выходной фактор более ничего не оказывает влияния.

Для описания систем, представленных в виде “черного ящика” успешно используется полиноминальная модель, дающая возможность учитывать множество входных факторов. Зависимость выхода технологического процесса (вектора отклика Y) в данной модели от входных факторов x_i , x_j и т.д. определяется формулой:

Y = + + + + ….

Таблица 1

№ опыта	Факторы				Взаимодействия			Результаты опытов					Среднее значение
	x1	x2	x3	x1x2		x1x3	x2x3	y1	y2	y3	y4	i
1	+	+	+	+		+	+	0,12	0,10	0,11	0,14	0,1175
2	+	+		+				0,06	0,05	0,07	0,08	0,065
3	+		+			+		0,19	0,18	0,22	0,20	0,1975
4		+	+				+	0,19	0,16	0,18	0,16	0,1725
5	+						+	0,13	0,12	0,14	0,16	0,1375
6		+				+		0,11	0,12	0,09	0,10	0,105
7			+	+				0,24	0,23	0,22	0,21	0,225
8				+		+	+	0,12	0,11	0,10	0,13	0,115

2. Построение математической модели тп методом пфэ.

Полиноминальная модель технологического процесса для трех входных факторов определяется из уравнения:

y =

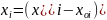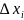/ – безразмерная величина;

– центр плана;

– интервал варьирования по i-му фактору.

1. Матрица планирования типа ПФЭ представлена таблице 1.

Таблица 1

№ опыта	Факторы				Взаимодействия			Результаты опытов					Среднее значение
	x1	x2	x3	x1x2		x1x3	x2x3	y1	y2	y3	y4	ξ
1	+	+	+	+		+	+	0,12	0,10	0,11	0,14	0,1175
2	+	+		+				0,06	0,05	0,07	0,08	0,065
3	+		+			+		0,19	0,18	0,22	0,20	0,1975
4		+	+				+	0,19	0,16	0,18	0,16	0,1725
5	+						+	0,13	0,12	0,14	0,16	0,1375
6		+				+		0,11	0,12	0,09	0,10	0,105
7			+	+				0,24	0,23	0,22	0,21	0,225
8				+		+	+	0,12	0,11	0,10	0,13	0,115

Здесь

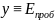
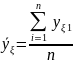– среднее значение результатов параллельных опытов.

ξ=1,….,N; N=8; n=4. По данным таблицы проводим следующие вычисления:

2) Определяем дисперсию среднего арифметического внутри выборки.

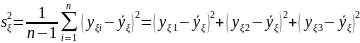
Расчеты и конечные результаты дисперсии среднего арифметического внутри выборки приведены в таблице 2.

Таблица 2

№	Результаты опытов					Сред. знач.		1		2		3		4		Дисперсия ср. арифм.
	y1	y2	y3	y4	ξ
1	0,12	0,10	0,11	0,14	0,1175		0,00000625		0,00030625		0,00005625		0,00050625		0,0002917
2	0,06	0,05	0,07	0,08	0,065		0,00002500		0,00022500		0,00002500		0,00022500		0,0001667
3	0,19	0,18	0,22	0,20	0,1975		0,00005625		0,00030625		0,00050625		0,00000625		0,0002917
4	0,19	0,16	0,18	0,16	0,1725		0,00030625		0,00015625		0,00005625		0,00015625		0,000225
5	0,13	0,12	0,14	0,16	0,1375		0,00005625		0,00030625		0,00000625		0,00050625		0,0002917
6	0,11	0,12	0,09	0,10	0,105		0,00002500		0,00022500		0,00022500		0,00002500		0,0001667
7	0,24	0,23	0,22	0,21	0,225		0,00022500		0,00002500		0,00002500		0,00022500		0,0001667
8	0,12	0,11	0,10	0,13	0,115		0,00002500		0,00002500		0,00022500		0,00022500		0,0001667

3) Осуществляем проверку однородности дисперсий по критерию Кохрена.

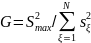
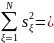0,00176667

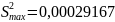
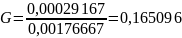
4) Находим критическое значение критерия Кохрена и проверяем гипотезу о равенстве выборочных дисперсий при р = 0,05.

ν₁=n-1=4-1=3; ν₂=N=8

Из таблицы Кохрена на пересечении ν₁ и ν₂ табличное значение G_табл=0,4377, G≤ G_табл, поэтому гипотеза о равенстве выборочных дисперсий верна (с определенной степенью риска р = 0,05), т. е. эксперименты воспроизводимы.

0,165096 ≤ 0,4377

5) Рассчитываем коэффициенты полинома.

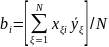
b₀ = 1/8(0,1175 + 0,065 + 0,1975 + 0,1725 + 0,1375 + 0,105 + 0,225 + 0,115) = 0,141875

b₁ = 1/8(0,1175 + 0,065 + 0,1975 - 0,1725 + 0,1375 - 0,105 - 0,225 - 0,115) = -0,0125

b₂ = 1/8(0,1175 + 0,065 - 0,1975 + 0,1725 - 0,1375 + 0,105 - 0,225 - 0,115) = -0,026875

b₃ = 1/8(0,1175 - 0,065 + 0,1975 + 0,1725 - 0,1375 - 0,105 + 0,225 - 0,115) = 0,03625

b₁₂ = 1/8(0,1175 + 0,065 - 0,1975 - 0,1725 - 0,1375 - 0,105 + 0,225 + 0,115) = -0,01125

b₁₃ = 1/8(0,1175 - 0,065 + 0,1975 - 0,1725 - 0,1375 + 0,105 - 0,225 + 0,115) = -0,008125

b₂₃ = 1/8(0,1175 - 0,065 - 0,1975 + 0,1725 + 0,1375 - 0,105 - 0,225 + 0,115) = -0,00625

b₁₂₃ = 1/8(0,1175 - 0,065 - 0,1975 - 0,1725 + 0,1375 + 0,105 + 0,225 - 0,115) = 0,004375

6) Определяем значимость найденных коэффициентов по критерию Стьюдента.

k=N(n-1)=8(4-1)=24 и p=0,05

По таблице t-распределения ищем t_кр, где столбец слева это k, а верхний столбец – p.

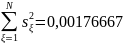
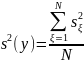
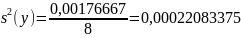
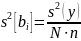
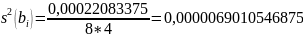
s(b) = 0,00262698585597638876971544732021≈ 0,002626985856

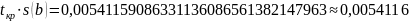
Те значения коэффициентов, которые меньше 0,0054116 являются незначимыми, то есть если |b_i| < 0,0054116, то коэффициент признается незначимым.

В нашем случае это коэффициент b₁₂₃.

Таким образом, математическое описание функции отклика в заданной области имеет вид:

y = 0,141875 - 0,0125x₁ - 0,026875x₂ + 0,03625x₃ - 0,01125x₁x₂ - 0,008125x₁x₃ - 0,006256x₂x₃

7) Производим проверку адекватности полученной модели, вычислив теоретические значения функции отклика 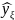. Это значит, меняем знак перед переменной в уравнении, исходя из таблицы 1.

Значения :

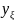y₁= 0,113125

y₂= 0,069375

y₃= 0,201875

y₄= 0,176875

y₅= 0,133125

y₆= 0,100625

y₇= 0,220625

y₈= 0,119375

Дисперсия адекватности определяется из выражения

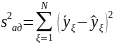
Значение берем из таблицы 1 это среднее значение результатов параллельных опытов.

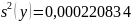
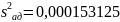
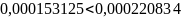
_{Так как , то можно сделать вывод о том, что разработанная математическая модель адекватна исследуемому технологическому процессу и может использоваться в заданной области для оптимизации его параметров.}