5. Исследование фазовых траекторий на участках постоянства управления

I. Пусть n_y = +n_ym. Подставим n_y в исходную систему (4.1), получим:

; (5.1)

; (5.2)

. (5.3)

Для сокращения математических выкладок примем следующее обозначение:

(5.4)

Перейдя от (5.1) и (5.2) к переменной интегрирования получим:

= x(t) = x +R sin | =>

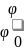(5.5)

Перенесём x влево. Складывая их, получим уравнение движения в явной форме:

(x )² + (y )² = R². (5.6)

Фазовые траектории на данном участке представляют семейство окружностей с центром в точке ( ), зависящих от начальных условий. Обозначим семейство окружностей через T⁺ и заметим, что движение по ним осуществляется по часовой стрелке.

x_o, y_o и – начальные условия для участка траектории (нельзя путать эти условия с начальными условиями для полной фазовой траектории)

Рис. 3.

II. Пусть n_y = - n_ym. Рассуждая по аналогии, покажем, что семейство фазовых траекторий T^- на этом участке будет иметь вид:

(x )² + (y )² = R², где

x_ц = x_o + Rsin и

y_ц = y_o - Rcos

Рис. 4.

Семейство фазовых траекторий T^- на этом участке будет иметь вид:

(x )² + (y )² = R², (5.7)

где x_ц = x_o +Rsin ;

y_ц = y_o - Rcos

III. Пусть n_y =0 - особый режим, тогда

;

= _o.

= tg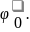

Из условия (4.8) следует, что в особом режиме угол наклона фазовых траекторий будет равен:

γ = arctg .

Рис. 5.

Движение в особом режиме осуществляется по прямой, проходящей через центр окружности, то есть, через начало координат.

Полная оптимальная фазовая траектория состоит из дуг (отрезков) окружностей T⁺, T^-

и прямых T⁰.

6. Исследование полных оптимальных фазовых траекторий

Для определения числа участков траекторий и точки переключения с одного участка на другой, необходимо исследовать условия переключения фазовых траекторий.

Начнём исследование с этой задачи: найдём из сопряжённой системы. Проинтегрировать выражение для не получается, так как функция не известна.

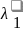= Vsin (6.1)

Представим выражение (6.1) в следующем виде: = , тогда

(t)= , где (6.2)

=const, =const из сопряжённой системы.

Постоянно интегрируя, С находится из условия t=T: C= - y(T) + x(T)+ (T).

Подставим сюда выражение для (T), (T); (T)-условие трансверсальности; получим:

С = ... = 0 (6.3)

Получим выражение для функции переключения как функцию фазовых координат. Из (6.1) и (6.3) следует:

= y + x = (x, y)=0 (6.4)

(6.4) – уравнение линии, на которой происходят переключения. Линия представляет собой прямую, проходящую через начало координат и имеющую наклон:

tgφ = . (6.5)

Рассмотрим фазовые траектории с точки зрения её геометрических свойств.

Рис. 6. Рис. 7.

Из вышеизложенного делаем следующие выводы:

- n_o(t) имеет разрыв 1-го рода, следовательно функция φ(t) является непрерывной, но может иметь угловые точки, следовательно x(t) и y(t) являются гладкими, следовательно полная оптимальная фазовая траектория является гладкой кривой на плоскости x и y.

- это говорит о том, что в точках сорпяжения участков траекторий на предыдущем участке траекторий траектория на предыдущем участке касается траектории на последующем участке, то есть либо окружности касаются друг друга, либо касаются окружность и прямая (Рис. 7).

Получается условие переключения на фазовой плоскости:

- . (6.6)

Рассмотрим логику оптимального поведения объекта.

Согласно принципу максимума, вдоль оптимальной траектории H(t)=const на интервале [t_o; T].

Согласно условию трансверсальности: H(t)= =1, откуда следует, что H(t)=const=1.

Запишем выражение для гамильтониана в виде:

(6.7)

Тогда = - откуда в особом режиме .

Таким образом, геометрической целью поведения объекта является совмещение вектора скорости самолёта с линией переключения.

В случае невыполнения условий управление выполняется таким образом, чтобы оптимизировать движение, то есть, совместить движение с линией переключения.

Из (4.7) следует, что в особом режиме фазовая траектория имеет наклон:

φ=arctg .

Таким образом, фазовая траектория линии переключения либо совпадает, либо параллельна. Очевидно, что во втором случае фазовая траектория не встретится с линией переключения, следовательно, особый режим может начинаться в точке касания фазовой траектории с линией переключения.

Рассмотрим особый режим движения.

Движение вдоль линии переключения осуществляется в направлении от центра или у центру. Исходя из того, что целью поведения является выполнение условий прицеливания (D=R_n), вектор скорости направлен на цель, поэтому можем утверждать, что задача объекта состоит в следующем:

- как можно быстрее выйти из круга R_n;

- как можно быстрее выполнить разворот, вектор скорости был направлен на цель.

Выводы:

- если в особом режиме движение осуществляется от цели (центра), то оно может продолжаться до выхода на окружность R_n;

- если движение осуществляется к центру, то самолёт находится в зоне, откуда возможно выполнение условия прицеливания для первой атаки;

- если имеет место выход на окружность R_n в особом режиме, то вектор скорости нормален к окружности R_n.

Для того, чтобы понять логику дальнейшего движения объекта, введём в рассмотрение семейства окружностей и , обладающих следующими свойствами:

а) если мы движемся в особом режиме внутри окружности по траектории в направлении центра, то участкок особого будет предпоследним, а последний участок будет траекториями или ;

б) это позволяет определить геометрическое место точек вне окружности R_п, полные оптимальные траектории повторной атаки, которые будут состоять из одного участка

Для этого достаточно найти точки касания с вертикалью (параллельно оси х). Эти точки образуют окружность с радиусом R.

Таким образом, если в системе имеет место особый режим, то последующий участок полной траектории является последним (с точки зрения критерия это будет безразлично).

Заметим, если точка касания луча, исходящего из центра, с начальными фазовыми траекториями или , находится за пределами круга R_n, то особого режима не будет, и в указанной точке касания будут происходить переключения с на или наоборот.

Рис. 8.

Последние участки фазовых траекторий будут проходить только по траекториям и , как наиболее короткое по времени движение.

Очевидно, что (это показывает решение других постановок задач быстродействия) оптимальная траектория выхода на границы R_n может состоять либо из одного либо из двух участков, имеющих следующую структуру:

{ }, { }, { };

{ }, { }.

В зависимости от положения начальной точки выделяют геометрические места в плоскости повторной атаки, каждые из которых соответствуют определённой структуре полной фазовой траектории.

Всё вышеизложенное позволяет для каждой начальной точки повторной атаки определить структуру полной оптимальной траектории (число участков последовательного переключения, см. рис. 9 далее).