МОСКОСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ)

Факультет №7 «Робототехнические и интеллектуальные системы»

Кафедра №703 «Системное проектирование авиакомплексов»

Учебно-исследовательская работа на тему: «Исследование траектории повторной атаки истребителя-бомбардировщика»

Выполнил: студент группы 07-406с

Авсюкевич Д. С.

Руководитель: кандидат технических наук,

доцент кафедры № 703

Прохоров И. А.

Москва 2014

1. Постановка задачи

При выполнении боевой задачи, состоящей в поражении наземной цели путем нанесения по ней бомбового удара, истребитель-бомбардировщик (штурмовик) способен по различным причинам не выполнить условия бомбометания в первой атаке (не разведанная ранее цель, запоздалое её обнаружение) или не поразить цель (промах). В таких случаях требуется провести повторную атаку в условиях, как правило, противодействия системы местной ПВО противника.

Для уменьшения вероятности поражения атакующего самолёта средствами ПВО, необходимо стараться уменьшить время пребывания его в зоне их действия и, следовательно, выполнить маневр повторной атаки как можно быстрее. Таким образом, важно определить оптимальные по быстродействию траектории повторной атаки.

Будем считать, что для выполнения самолётом условий прицеливания при бомбометании необходимо, чтобы линия его пути на земле оказалась направленной точно в цель (пренебрегая ветром), а его расстояние от цели, отчитываемое по линии пути, было не менее заданного значения, равного R­­_n. При этом начальное положение самолёта при выполнении повторной атаки (в проекции на поверхности Земли) может находиться как внутри, так и вне круга радиусом R_n и с центром в точке цели (начальная точка траектории повторной атаки может находится вне круга в тех случаях, когда после обнаружения цели для выполнения прицеливания необходимо совершать отворот в направлении от цели, так как разворот в сторону цели приводит к вхождению в круг без выполнений условий прицеливания).

Заметим, что направление вектора скорости в момент начала повторной атаки, без ущерба для общности полученного результата, можно рассматривать всегда совпадающим с направлением одной из осей декартовой системы координат с центром в точке цели, так как при любом другом направлении эту задачу можно свести к первой выбором другой системы координат (рис. 1).

Заметим, что при решении данной задачи особый интерес представляет нахождение оптимального закона управления с обратной связью, позволяющего реализовать оптимальные по быстродействию траектории повторной атаки для любых начальных условий.

Формализуем данную задачу.

Рис. 1

2. Формализация задачи

Пусть движение самолета в горизонтальной плоскости описывается следующей системой дифференциальных уравнений (в системе координат с началом в точке цели):

(2.1)

x, y – декартовы координаты летательного аппарата;

– угол между вектором скорости V и осью x;

V – модуль скорости.

Управляющую перегрузку будем считать подчинённой следующему ограничению:

|n_y(t)| n_ym (2.2)

В момент окончания повторной атаки t=T точка [x(T), y(T)] должна принадлежать окружности с радиусом, равным R_n, и с центром в начале координат, а вектор скорости (T) должен быть направлен в центр этой окружности, то есть должны выполняться условия:

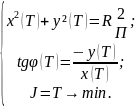(2.3)

Таким образом, математическая постановка задачи состоит в следующем:

1) найти оптимальный процесс {n (t), x^o(t), y^o(t), ^o(t)}, переводящий за минимальное время систему (2.1) из начального положения (x_o, y_o, 0) на конечное многообразие в пространстве фазовых координат (x, y, ), определяемое соотношением (2.3), и удовлетворяющий ограничению (2.2);

2) найти оптимальный закон управления с обратной связью n (x, y, ), решающий задачу оптимального перевода системы на терминальное многообразие из любой начальной точки.

Данная задача относится к классу задач оптимизации управления детерминированных динамических систем с фиксированным левым концом, подвижным правым, с ограничением на управление вида неравенства и критерием-временем процесса. Задача нахождения оптимального процесса {n^o(t), x^o(t), y^o(t), ⁰(t)}является задачей оптимально программного управления, а задача нахождения оптимального закона управления с обратной связью-задачей оптимального координатного управления. Первая задача может быть решена на основе теоремы «Принципа максимума» Л.С. Пантрягина.

3. Метод решения задачи.

Теорема «Принцип максимума»

3.1. Общая постановка задачи оптимального

программного управления при наличии ограничений

общего вида на управляющие переменные

Пусть движение динамической системы координат описывается дифференциальным уравнением вида:

ẏ=f(y, u, t), (3.1.1)

где y=(y₁, y₂, … , y_n) - вектор фазовых координат

u=(u₁, u₂, … , u_r) – вектор управляющих параметров,

f – вектор-функция, определённая при всех допустимых значениях y, u,

Начальная и конечная фаза движения системы удовлетворяют граничному условию вида:

w[t_o, y(t_o), T, y(t_o)]=0, (3.1.2)

где w=( w₁, w₂, … , w_l)- вектор функция краевых условий, непрерывно дифференцируемая по всем своим аргументам.

Критерий оптимальности имеет вид:

I=g[y(t_o), t_o, y(T), T]+ (3.1.3)

Вектор управления u(t) подчинён следующим ограничениям:

u(t) Ω_uE^r, (3.1.4)

где Ω_u – замкнутая ограниченная область в евклидовых пространствах соответствующей размерности. Функция Ω_u считается допустимой, если она кусочно-непрерывна и удовлетворяет условию (3.2.1, см. далее). Для удобства введём в рассмотрение вспомогательные построения и термины.