Тема: Проектування цифрового автомата з пам'яттю

Мета: Навчитися проектувати цифрові автомати з пам'яттю

Завдання: Спроектувати цифровий автомат Мілі згідно заданих таблиць переходів і виходів. Комбінаційну схему збудження і комбінаційну схему формування вихідних сигналів реалізувати в заданому базисі І-НІ тип триггера – JK

Вхідні дані:

Таблиця 1 - Таблиця переходів

Вхідні дані	Стан автомата
	S1	S2	S3	S4	S5
X1	S5	-	S2	S1	S4
X2	S2	S1	S5	S3	S1
X3	S3	S3	-	-	S5
X4	S5	S1	S4	S2	-

Таблиця 2 - Таблиця виходів

Вихідні дані	Стан автомата
	S1	S2	S3	S4	S5
X1	Y6	-	Y5	Y6	Y2
X2	Y1	Y2	Y4	Y1	Y2
X3	Y3	Y2	-	-	Y5
X4	Y6	Y1	Y2	Y1	-

Зміст

	Тема. Мета. Завдання. Вхідні дані.	2
	Зміст	3
1	Теоретичні відомості	4
2	Порядок виконання роботи	6
2.1	Кодування	6
2.2	Вибір елементів пам'яті автомата	7
2.3	Побудова функії збудження триггеру	8
2.4	Мінімізація функії збудження триггеру	9
2.5 2.6 2.7	Побудова комбінаційної схеми №1 Мінімізація функцій виходів Побудова комбінаційної схеми №2	11 12 13
	Висновки	14
	Література	15

1. Теоретичні відомості

Вузли і пристрої, які містять елементи пам’яті відносяться до класу автоматів з пам’яттю.

Цифровий автомат – це пристрій, який здійснює приймання, зберігання і перетворення дискретної інформації за деяким алгоритмом.

Абстрактний цифровий автомат A визначається сукупністю п’яти

об’єктів {X, S, Y, ϕ, λ}, де X = { хi }, i Є1, m – множина вхідних сигналів

автомата А (вхідний алфавіт автомата А); S = { sj } , j Є 1, n – множина станів автомата А (алфавіт станів автомата А); Y = { yk } , k Є 1, l – множина вихідних сигналів автомата А (вихідний алфавіт автомата А); ϕ – функція переходів автомата А, яка відображає (X*S)→S, тобто ставить у відповідність будь-якій парі елементів добутку множин (X*S) елемент множини S; λ – функція виходів автомата А, яка задає відображення (X*S)→Y або S→Y.

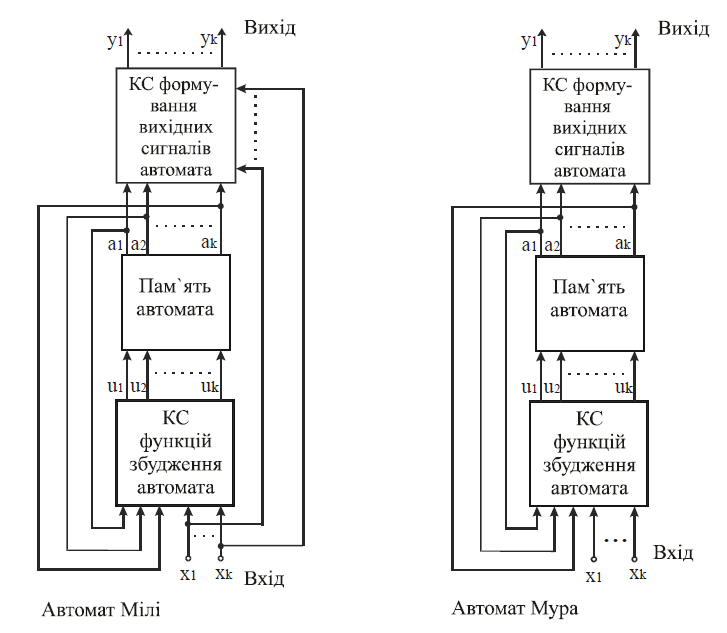
За способом формування функції виходів розрізняють наступні типи

автоматів: автомат Мілі, автомат Мура.

Розрізняють два класи автоматів : Асинхроні та синхроні. Синхронний автомат характеризується тим, що функціонує під управлінням тактових сигналів – ТС, з постійною тривалістю t_TC та постійною частотой F_TC, якщо кантування часу рівномірне . В асинхронних автоматах тривалість інтервалу часу протягом якого залишається незмінним стан вхідних сигналів, являєтся величиной зміной та определяется часом, який необхідно автомату для встановлення відповідних вихідних сигналів и завершеня переходу в новий стан.

В абстрактному автоматі Мілі функція виходів λ задає відображення:

(X*S)→Y.

Автомат Мілі характеризується системою рівнянь:

y(t) = λ[s(t),x(t)];

s(t +1) = ϕ[s(t),x(t)].

Автомат Мура – системою рівнянь:

y(t) = λ[s(t)];

s(t +1) = ϕ[s(t),x(t)].

Рис 1 - Структура автоматів Мілі та Мура

2. Порядок виконання роботи

1. Кодування

Кодування це – процес заміни букв алфавітів X,Y,S цифрового автомата двійковими векторами

Цей процес описується таблично (табл. 3, табл. 4, табл.5) у лівій частині таблиці перераховуються всі букви (наприклад вхідного алфавіту), а в правій – двійкові вектори, які ставляться у відповідність цим буквам.

Таблиця 3 - кодування У

	W1	W2	W3
y1	0	0	0
y2	0	0	1
y3	0	1	1
y4	0	1	0
y5	1	1	0
y6	1	1	1

Таблиця 4 - кодування Х

	Z1	Z2
x1	0	0
x2	0	1
x3	1	1
x4	1	0

Таблиця 5 – кодування S

	Q1	Q2	Q3
s1	0	0	0
s2	0	0	1
s3	0	1	1
s4	0	1	0
s5	1	1	0

Таблиці переходів та виходів після кодування мають вигляд:

Таблиця 6 – Кодована таблиця переходів

	Z1	Z2	S1	S2	S3	S4	S5
X1	0	0	110	-	001	000	010
X2	0	1	001	000	110	011	000
X3	1	1	011	011	-	-	110
X4	1	0	110	000	010	001	-

Таблиця 7 - Кодована таблиця виходів

	Z1	Z2	S1	S2	S3	S4	S5
X1	0	0	111	-	110	111	001
X2	0	1	000	001	010	000	001
X3	1	1	011	001	-	-	110
X4	1	0	111	000	001	000	-