№ 19 Емтихан билеті

1. Үш фазалы тізбектің активті қуаты

2. Синусоидалы шамалардың мәндері

3. Суретте көрсетілген электр схемасының параметрлері: U_Л=127 B, R_а=8 Ом, R_б=8 Ом, R_с=8 Ом, х_а=6 Ом, х_б=6 Ом, х_с=6 Ом. Осы параметрлер және сызықты кернеу арқылы фазалық тоқтарды және барлық тізбектің жеке бөліктері үшін активті қуатты анықтау керек.

1) Үш фазалы тізбектің активті қуаты жүктеменің фазаларының активті қуаттарының және нөлдік сымның кедергісінде бөлінетін активті қуаттың қосындысына тең:

,[Вт].

Үш фазалы тізбектің реактивті қуаты:

, [ВАр].

Толық қуат: , [ВА].

Жүктеме симметриялы болса болса, онда: , , , .

Фазалық активті қуат: ; Фазалық реактивті қуат: . Үш фазалы тізбектің активті және реактивті қуаты: , .

Үш фазалы тізбектің толық қуаты: ;

Жүктеменің фазаларының өзара жалғану сұлбаларына ( жұлдызша немесе үшбұрыш) байланыссыз үш фазалы тізбектің қуаттарын желілік кернеу мен желілік ток арқылы анықтауға болады.: , , ;

2) а) Амплитудалық мән ( Im, Um, Em ); ә) Лездік мән ( i, u, e ) - синусоидалы шаманың кез келген сәттегі мәні: i=Imsin( t+ _i); u=U_msin( t+ _u); e=E_msin( t+ _e); б) Орташа мән (I_ор, U_ор, E_ор) - синусоидалы шаманың жарты период ішіндегі орташа мәні:

I_ор= = = 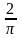I_m=o.638I_m: U_ор= = U_m=0.638U_m.

Сонымен орташа мән амплитудалық мәннен π/2 есе аз.

в)Әрекеттік мән ( I, U, E ) немесе орташа квадраттық мән

I= = = I_m/ =0.707I_m, сол сияқты U= U_m/ = 0.707U_m, Е=0.707E_m.

№ 20 Емтихан билеті

1. Үш фазалы жүйенің артықшылықтары

2. Синусоидалы шамаларды бейнелеу жолдары

3. Суретте көрсетілген электр схемасының параметрлері: U_Л=127 B, R_аб=5 Ом, R_СА=6 Ом, х_аб=10 Ом, х_бс=8 Ом, х_са=4 Ом. Осы параметрлер және сызықты кернеу арқылы фазалық тоқтарды, сызықты тоқтарды, барлық тізбектің жеке бөліктері үшін активті қуатты анықтау керек.

1) а) Электр энергиясын бір фазалық жүйемен алыс қашықтыққа жеткізу үшін қажетті алты сым орнына үш фазалық жүйемен тасымалдағанда небәрі үш сым ғана керек болады, яғни үш фазалық жүйемен тасымалдаған экономикалық жағынан тиімді;

б) Үш фазалы электр қондырғылары құрылысы жағынан қарапайым , бағасы арзан, жұмыс істеуі сенімді болады;

в) Үш фазалы жүктеме симмериялы болса, онда жүйенің лездік куатының мәні период ішінде өзгермейді.

2) а) Тригонометриялық функциялар арқылы бейнелеу: i=I_msin( t+ _i) ; u=U_msin( t+ _u);

ә) Тікбұрыштық координаталарда уақыттық диаграмма арқылы бейнелеу ( 10-сурет);

б) Айнымалы вектор арқылы бейнелеу. Тікбұрыштық координаталар жазығында ұзындығы синусоидалы токтың i=I_msin( t+ ) амплитудасына I_m тең вектор тең бұрыштық жылдамдықпен айналып тұр делік (11-сурет). Бастапқы жағдайда вектор абцисса осінен бұрышына ығысқан. Уақыт өткен сайын вектор t жылдамдығымен айналып, шеңбер сызып шығады Егер вектордың әрбір сәттегі ордината осіндегі проекциясыларын уақыттық диаграмма түрінде бейнелесек, онда проекцияның синусоидалы заңдылықпен өзгеретіндігін көреміз, яғни вектордың ордината осіндегі проекциясының уақытқа тәуелді өзгерісі синусоидалы шаманың лездік мәндерін өзгерісін сипаттайды. Демек, синусоидалы шаманы ұзындығы оның амплитудасына тең, жылдамдығы оның бұрыштық жиілігіне тең айналмалы вектор түрінде бейнелеуге болады. Вектордың бастапқы жағдайы синусоидалы шаманың бастапқы фазасымен анықталады. Бұрыштық жиілігі бірдей бірнеше синусоидалы шамалардың векторлары бірдей жылдамдықпен айналады. Сондықтан олардың өзара орналасуы өзгермейді. Сол себепті практикада оларды айналдырмайды, оларды бастапқы фазаларына сәйкес жазықтықта өзара орналастырады. Векторларды айналдыру қажеттігі болмағандықтан координаталар осьтерін көрсетудің қажеті болмайды. Бірінші векторды горизонталь немесе вертикал орналастырады да, қалғандарын бастапқы фазаларына сәйкес осы векторға байланысты орналастырады.

Синусоидалы шамалардың векторларлар түрінде бейнелеу оларды геометриялық жолмен қосу немесе алу операциясын орындауға мүмкіндік береді.

в) Синусоидалық шамаларды комплекс сандар арқылы бейнелеу. Синусоидалы шама тригонометиялық функция түрінде берілсін: i=I_msin( t + φ). Комплекстік жазықтыққа ұзындығы амплитудаға I_m тең, ал нақты осьпен құрайтын бұрышы бастапқы фазаға φ тең вектор саламыз (12- сурет). Бұл вектордың ұшы белгілі бір комплекс санға - синусоидалы шаманың комплекстік амплитудасына сәйкес келеді. I_m = I_me^j - комплекстік амплитуда.Уақыт өткен сайын фаза өседі де, бұл вектор айналмалы векторға айналады: I_me^{j( t+ )}= I_mcos( t+ )+ jI_msin( t+ ). Жорамал бөлік синусоидалы шамаға тең, яғни синусоидалы шаманы комплекс санның жорамал бөлігі арқылы көрсетуге болады.

Синусоидалы шамаларды комплекстік жазықтықта векторлар арқылы көрсету оларды қосып, алуға (геометриялық жолмен) мүмкіндік береді.