№ 1емтихан билеті

1. Электр тізбегінің жіктелуі

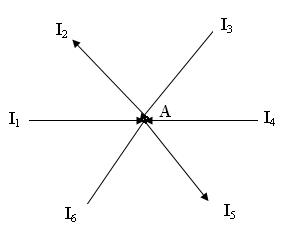
2. “А” түйіні үшін кирхгофтың 1 заңы бойынша теңдеу жазыңыз.

3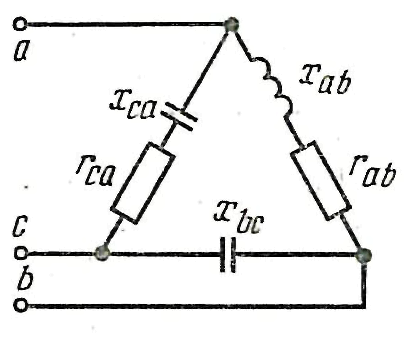 . Суретте көрсетілген электр схемасының параметрлері: U_С=127 B, R_аб=5 Ом, R_СА=6 Ом, х_аб=10 Ом, х_бс=8 Ом, х_са=4 Ом. Осы параметрлер және сызықты кернеу арқылы фазалық тоқтарды, сызықты тоқтарды, активті қуатты анықтау керек.

1) Электр тізбегінің жіктелуі. а) токтың түріне байланысты: тұрақты ток тізбектері, айнымалы ток тізбектері, бір фазалы, үш фазалы және көп фазалы ток тізбектері; ә) тізбектің элементтерінің вольтамперлік сипаттамасына байланысты: сызықты және сызықты емес электр тізбектері; б)тізбектегі электр энергиясы көздерінің (қоректендіргіштердің) санына байланысты: бір қоректендіргіші бар және бірнеше қоректендіргіші бар электр тізбектері; в) элементтерді өзара жалғау әдістеріне байланысты: тармақталмаған және тармақталған тізбектер.

2) Сұлбалардағы түйіндердің потенциалдарын белгісіз ретінде қабылдап, электр тізбектерін есептеу тәсілін түйіндік потенциалдар тәсілі деп атайды.Айталық, сұлбада n-түйін болсын. Сұлбаның кез-келген бір нүктесін ойша жермен қосамыз, яғни оның потенциалын нөлге тең деп аламыз.Соның нәтижесінде белгісіздер саны n-1-ге дейін азаяды. Бұл тәсіл бойынша теңдеулер Кирхгофтың бірінші заңы бойынша түйінде түйіскен токтарға арнап құрылады. Токтарды түйіндердің потенциалдары арқылы Ом заңы бойынша өрнектеуге болады. Нәтижесінде теңдеулер жүйесі мынадай түрде жазылады:

φ₁G₁₁ + φ₂G₁₂ + φ₃G₁₃= I₁₁

φ₁G₂₁ + φ₂G₂₂ + φ₃G₂₃= I₂₂

φ₁G₃₁ + φ₂G₃₂ + φ₃G₃₃= I₃₃

φ₁, φ₂, φ₃- бірінші, екінші және үшінші түйіндердің потенциалдары; G₁₁, G₂₂, G₃₃-- бірінші, екінші және үшінші түйіндерде түйіскен тармақтардың өткізгіштердің қосындысы; G_km- k мен m түйіндерді байланыстыратын тармақтың өткізгіштігі, “минус” таңбасымен алынады; I₁₁, I₂₂, I₃₃- түйіндердің түйіндік токтары. Белгілі бір түйіннің түйіндік тогы сол түйінмен байланысқан тармақтардағы э.қ.к.-терді сол тармақтардың кедергілеріне бөлу арқылы табылған токтардың алгебралық қосындысына тең. Э.қ.к.-тері түйінге бағытталған тармақтардың токтары «плюс» таңбасымен алынады, ал керісінше жағдайда «минус»таңбасы алынады.

Берілген тізбектің (6-сурет) « г» түйінінің потенциалын нөлге тең деп аламыз.Теңдеулер көрсетілген тізбек үшін былай жазылады:

φ_а(g₁+g₃+g₆) - φ_бg₁ - φ_вg₆= -E₁g₁-Е₃g₃

φ_б(g₁+g₂+g₅) - φ_аg₁ - φ_вg₂= E₁g₁ + E₂g₂

φ_в(g₂+g₄+g₆) - φ_бg₂ - φ_аg₆= -E₂g₂ -E₄g₄

Мұндағы g₁=1/R ₁, g₂=1/R₂, g₃=1/R₃ , g₄=1/R₄ , g₅=1/R₅ , g₆=1/R₆.

Теңдеулер жүйесін шешу арқылы φ_а, φ_б, φ_в табамыз. Токтардың мәндерін Ом заңы арқылы табамыз:

I₁= (E₁+ U_аб)/R₁ = [E₁+(φ_а - φ_б)]/R₁, I₂= (E₂+ U_вб)/R₂=[E₂+(φ_в- φ_б) ]/R₂, I₃= (E₃+ U_аг)/R₃=[E₃+ (φ_а - φ_г) ]/R₂

I₄= U_вг/R₄=(φ_в - φ_г)/R₄ = φ_в/R₄ I₅= U_бг/R₅=(φ_б - φ_г)/R₄ = φ_б/R₅ I₆= (E₆+ U_ав)/R₆=[ E₆+ (φ_а - φ_в) ]/R₆

№ 2 емтихан билеті

1. Э лектр тоғы деген не?

2. Кедергілері бірізді жалғанған электр тізбегі.

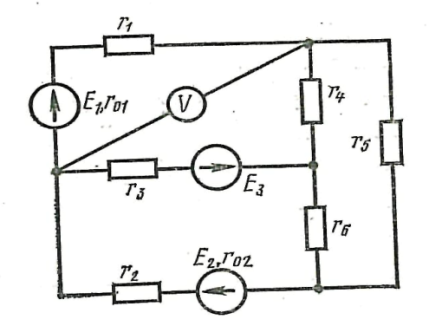
3. Суретте көрсетілген электр схемасының параметрлері: Е₁=72 В, Е₂=12 В, Е₃=4 В, r₀₁=0,7 Ом, r₀₂=1,5 Ом, r₁=6 Ом, r₂=1 Ом, r₃=10 Ом, r₄=4 Ом, r₅=12 Ом, r₆=4 Ом. 1. Схемаға кирхгофтың бірінші және екінші заңы бойынша теңдеу құр; 2. Барлық тармақтардың тоғын тап; 3. Кернеуді анықта; 4. Қуат балансын құр; 5. Есептің дұрыстығын тексер.

1. Электр тогы (Э.т) – электр қозғаушы күштің әсерінен зарядтардың (зарядталған бөлшектер немесе дене) бағытталған қозғалысы. Зарядталған бөлшектер: өткізгіштерде — электрондар, электролиттерде —иондар (катиондар мен аниондар), газда —иондар мен электрондар, арнайы жағдайдағы вакуумда — электрондар, жартылай өткізгіштерде —электрондар мен кемтіктер (электронды-кемтіктік өтімділік) болып табылады. Электр тогы энергетика саласында — энергияны алыс қашықтыққа жеткізу үшін, ал телекоммуникация саласында — ақпаратты шалғайға тасымалдау үшін қолданылады

2. Кедергілері бірізді жалғанған электр тізбегін есептеу үшін кедергілерді бір балама (эквивалент) кедергімен R_б айырбастаймыз (2-сурет). Бұл жағдайда тізбектегі ток I= U/R_б. Балама кедергінің R_б мәнін анықтау үшін Кирхгофтың екінші заңы бойынша теңдеу құрамыз: U=U₁+U₂+U₃, мұндағы U₁=I∙R₁ ; U₂=I∙R₂ ; U₃=I∙R₃ ; U = I∙R_б. Сонда I∙R_б=I∙R₁+ I∙R₂+ I∙R₃ = I(R₁+R₂+R₃). Бұл теңдеуден R_б=R₁+R₂+R₃. Егер кедергілер бірізді жалғанса, онда балама кедергінің мәні осы кедергілердің арифметикалық қосындысына тең.

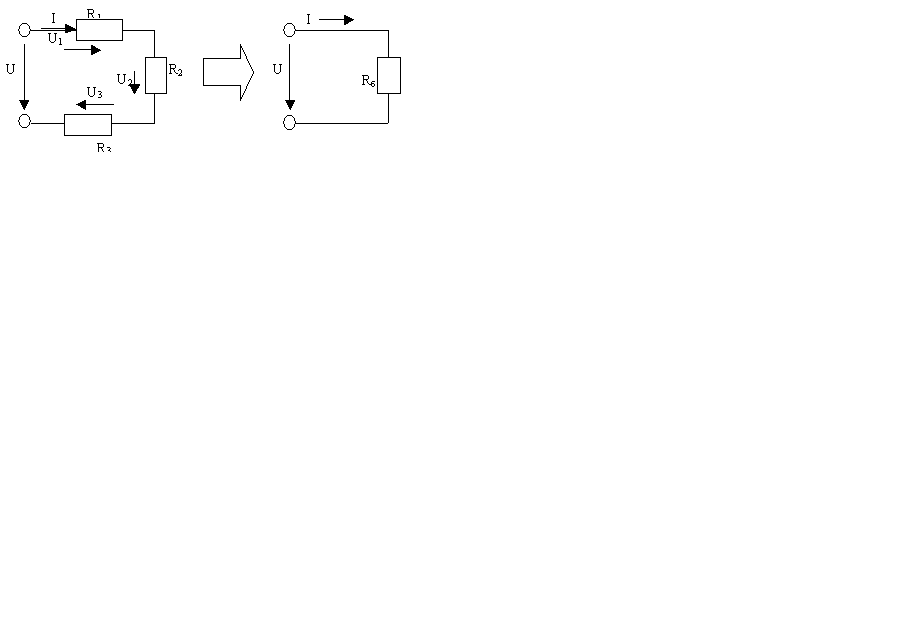
2-сурет

№ 3 емтихан билеті

1. Электр кедергісі деген не?

2. Кедергілері параллель жалғанған электр тізбегі

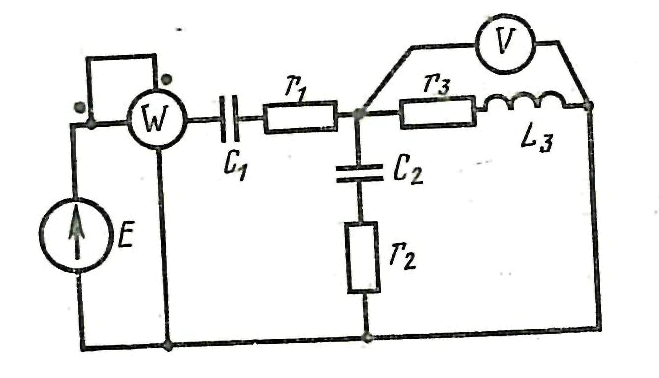
3. Суретте көрсетілген электр схемасының параметрлері: Е=220 B, f=50 Гц, С₁=637 мкФ, С₂=300 мкФ, L₃=15,9 мГн, R₁=8 Ом, R₂=3 Ом, R₃=4 Ом Барлық тізбектің тармақтарындағы тоқтарды, бөліктердің кернеуін, активті, реактивті және толық қуатты табу керек.

1) Электр кедергісі – өткізгіштің (немесе электр тізбегінің) электр тогының өтуіне қарсы әсерін сипаттайтын физикалық шама. Тұрақты ток өтетін тізбектің Э. к. активті (омдық), ал айнымалы ток тізбегіндегісі толық кедергі (омдық, сыйымдылық және индуктивтік кедергілердің қосындысы) деп аталады. Э. к. өткізгіштің материалына, оның пішініне, сыртқы жағдайларға т. б. тәуелді болады. Жиілік жоғарылағанда өткізгіштің сыртқы бетіндегі ток тығыздығының артуы кедергі шамасын көбейтеді. Меншікті Э. к. бірліктердің халықаралық жүйесінде (СИ) омѓм-мен өлшенеді. Электр тізбегіндегі ток шамасын реттеу немесе шектеу үшін қосылатын (жалғанатын) элементті (радиобөлшекті) кейде “Э. к.” деп те атайды. Мұның реттелетін түрі реостат; ал реттелмейтіндерінің бірі (тізбекке тізбектей жалғанатыны) қосымша кедергі, екіншісі (параллель жалғанатыны) шунт деп аталады.

2) Кедергілері параллель жалғанған электр тізбегін есептеу үшін кедергілерді бір балама (эквивалент) кедергімен R_б айырбастаймыз. Бұл жағдайда тізбектегі толық ток I= U/R_б. Балама кедергінің R_б мәнін анықтау үшін Кирхгофтың бірінші заңы бойынша теңдеу құрамыз. Параллель тармақтар саны үшеу болған жағдайда I=I₁+I₂+I₃, мұндағы I₁=U/R₁ , I₂=U/R₂ , I₃=U/R₃ – параллель тармақтардағы токтар. Сонда U/R_б=U/R₁+U/R₂+U/R₃. Бұл теңдеуден 1/R_б=1/R₁+1/R₂+1/R₃ немесе G_б=G₁+G₂+G₃, мұндағы G_б ,G₁ ,G₂ ,G₃ –тізбектің толық өткізгіштігі және параллель тармақтардың өткізгіштіктері. Жалпы жағдайда 1/R_б=1/ +1/R₂+1/R₃+...+1/ R_n , G_б=G₁+G₂+G₃+…+ G_n .

№ 4 емтихан билеті

1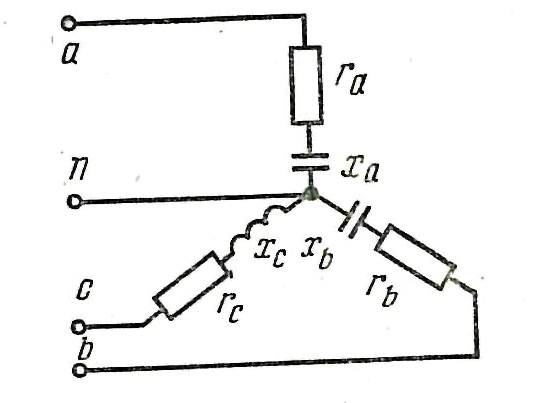 . Электр тізбегі үшін Ом заңы

2. Кедергілері аралас жалғанған электр тізбегі

3. Суретте көрсетілген электр схемасының параметрлері: U_Л=127 B, R_а=3 Ом, R_б=4 Ом, R_с=6 Ом, х_а=4 Ом, х_б=3 Ом, х_с=8 Ом. Осы параметрлер және сызықты кернеу арқылы фазалық тоқтарды және бейтарап тізбектегі (төрт тізбекті схема үшін) сызықты тоқтарды, барлық тізбектің жеке бөліктері үшін активті қуатты анықтау керек.

1) Ом заңы– электр тогының негізгі заңдарының бірі. Ом заңы – өткізгіштегі ток күшінің (І) осы өткізгіштің ұштары арасындағы кернеумен (U) байланысын анықтайды: U=r*І (1) мұндағы r өткізгіштің геометриялық өлшемдеріне, электрлік қасиеттеріне және температурасына байланысты болатын пропорционалдық коэффициенті r – омдық кедергі немесе өткізгіштің берілген бөлігінің кедергісі деп аталады. Ом заңын 1826 ж. неміс физигі Г. Ом (1787 – 1854) ашқан

2) Кедергілері аралас жалғанған электр тізбегін есептеу үшін алдымен параллель тармақтардың кедергісін бір балама кедергімен R₂₃ айырбастаймыз: 1/R₂₃=1/R₂+1/R₃. Сонан кейін R₁ мен R₂₃ бірізді жалғанғандықтан балама кедергімен R_б= R₁+ R₂₃ айырбастаймыз (3-сурет). Тізбектегі толық ток

I₁=U/R_б=U/( R₁+R₂₃).I₂ мен I₃ токтарын табу үшін U_аб кернеуін табамыз: U_аб=I₁ ∙R₂₃. Бұдан кейін токтарды табуға болады: I₂=U_аб/R₂ , I₃=U_аб/R₃ .

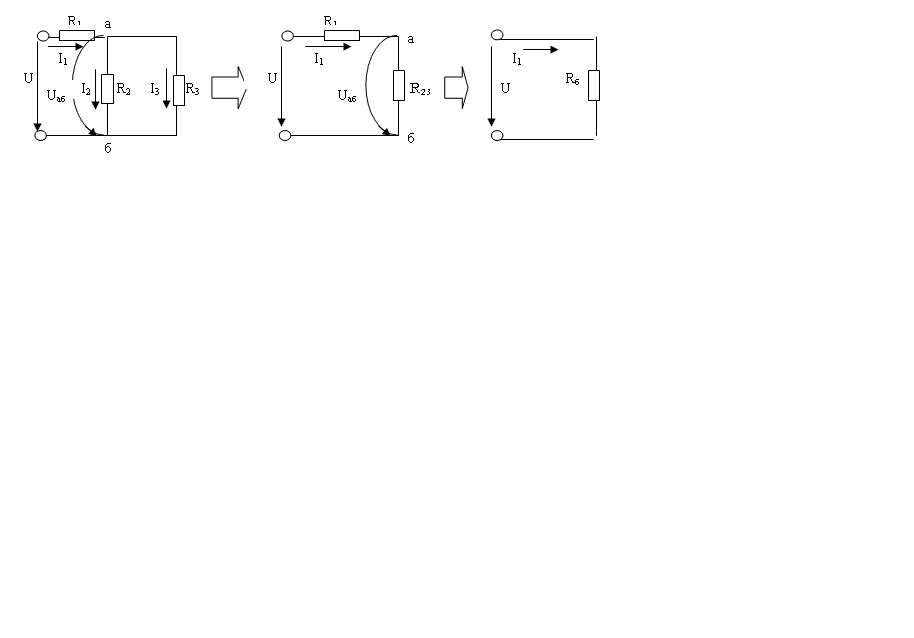
№ 5 емтихан билеті

1. К ирхгоф бірінші заңы

2. Беттестіру принципі

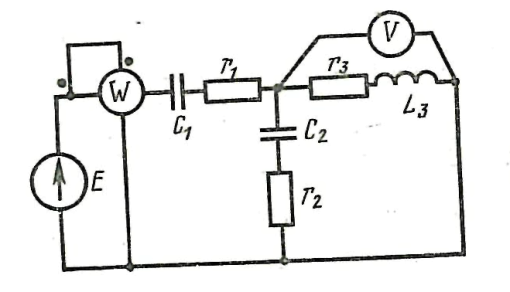
3. Суретте көрсетілген электр схемасының параметрлері: Е=200 B, f=50 Гц, С₁ =637 мкФ, С₂ =300 мкФ, L₃=15,9 мГн, R₁=8 Ом, R₂=3 Ом, R₃=4 Ом Барлық тізбектің тармақтарындағы тоқтарды, бөліктердің кернеуін, активті, реактивті және толық қуатты табу керек

1) Кирхгоф бірінші заңы. Бірінші анықтамасы: Тізбектің кез-келген түйінінде түйіскен токтардың алгебралық қосындысы нөлге тең. Математикалық түрде жазылуы: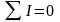 . Теңдеу құру үшін тұйінге кірген токтардың таңбасын «+» , ал шыққан токтардың таңбасын «-» етіп алу керек.

Екінші анықтамасы: Түйінге кірген токтардың арифметикалық қосындысы түйіннен шыққан тоқтардың арифметикалық қосындысына тең. Кирхгофтың бірінші заңы бойынша: I=I₁+I₂+I₃+I₄, немесе

(E_б – U_аб)/R_б =(E₁ – U_аб)/R₁+(E₂ – U_аб)/R₂ +(-E₃ – U_аб)/R₃+(E₄ – U_аб)/R₄. Бұдан

E_б= (E₁G₁+ E₂G₂-E₃G₃+E₄G₄ )/(G₁+G₂+G₃+G₄ ), 1/R_б=1/R₁+1/ R₂+1/ R₃+1/R₄= G₁+G₂+G₃+G₄.

Жалпы жағдайда У_б= /

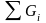
2) Беттестіру принципі өтпелі   прцесс  кезіндегі   ток  және   кернеу  еріксіз  және  еркін режимдеріндегі   процесс   болып   жіктеліп ,  олардың   қосын-дысына   тең   болады.

                    і = і _еркз + і _ерк  ;            u_R = u _Rеркз + u _Rерк

                               u_L = u _Lеркз + u _Lерк ;     u_C = u _Cеркз + u _Cерк                               (1.5)

Бұл   түзу  сызықты   электр  тізбегі  үшін  беттестіру  (наложение)  принципі  болып   саналады. Физикалық   тұрғыдан   қарағанда  тізбекте   тек   өтпелі   токтар   және   кернеулер   ғана   болады,  ал   оларды  еріксіз   және   еркін   құраушыларына   жіктеу   тек   математикалық  ыңғайлы   шешім   болып   саналады.  Ол   түзу   сызықты   электр  тізбектеріндегі   өтпелі   прцестерді   есептеуді   жеңілдетеді.  Шындығында   еркін   ток,  біртектес   дифференциалдық   теңдеудің   жалпы  шешімі   болып   есептеледі,   яғни   оның   шешімі   көрсеткіш   функ-циясы  Ae^pt   болып   саналады.  Бұл   өрнекке  А тұрақты   еселеуіші  кіреді,  оның   саны   дифференциалдық   теңдеудің  дәреже  көрсеткіш  ретіне  тең.

№ 6 Емтихан билеті

1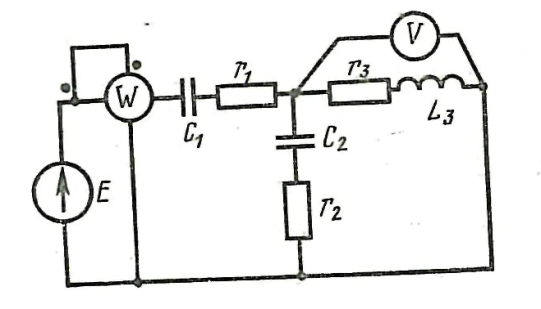 . Кирхгоф екінші заңы

2. Кедергілердің ұшбұрыштап және жұлдызша жалғануы және оларды балама түрлендірілуі

3. Суретте көрсетілген электр схемасының параметрлері: Е=200 B, f=50 Гц, С₁ =637 мкФ, С₂ =300 мкФ, L₃=15,9 мГн, R₁=8 Ом, R₂=3 Ом, R₃=4 Ом Барлық тізбектің тармақтарындағы тоқтарды, бөліктердің кернеуін, активті, реактивті және толық қуатты табу керек

1) Кирхгоф екінші заңы. Бірінші анықтамасы: Тұйық контурдағы э.қ.к.-тердің алгебралық қосындысы сол контурдағы кедергілердегі кернеулердің түсулердің алгебралық қосындысына тең. Екінші анықтамасы: Кез-келген тұйық контурдың бойындағы кернеулердің алгебралық қосындысына нөлге тең.

Математикалық түрде жазылуы: ,

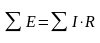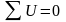
Кирхофтың екінші заңы бойынша теңдеу құрудың реті:

а) Тізбектің тармақтарындағы токтардың бағыттарын өз қалауымызша таңдап аламыз;

ә) Тізбектің контурларын айналу бағытын өз қарауымызша таңдап аламыз;

б) Э.қ.к.- тің алгебралық қосындысын тапқан кезде контурдағы э.қ.к.-нің бағыты контурды айналу бағытымен сәйкес келсе, онда оның таңбасы «+», ал керісінше жағдайда «-» болады;

в) Токтың бағыты контурды айналу бағытымен сәйкес келсе, онда кернеудің түсуінің таңбасы таңбасы «+», ал керісінше жағдайда «-» болады.

2) Кедергілердің ұшбұрыштап және жұлдызша жалғануы және оларды балама түрлендіру.

Кейбір жағдайларда есепті жеңілдету мақсатында ұшбұрыштап жалғанған кедергілерді жұлдызша жалғау сұлбасына түрлендіреді. Кейде керісінше түрлендіру де қолданылады. Түрлендіру кезінде мынандай шарттар орындалуы керек:а)Үшбұрыштың А,В,С түйіндеріндегі потенциалдар жұлдызшаның А,В,С потенциалына тең болуы керек; ә)Үшбұрыштың А,В,С түйіндеріне келетін токтар жұлдызшаның осы түйіндерге келетін токтарына тең болуы керек; б)Түрлендіру тізбектің басқа бөлігіне әсер етпеуі керек.

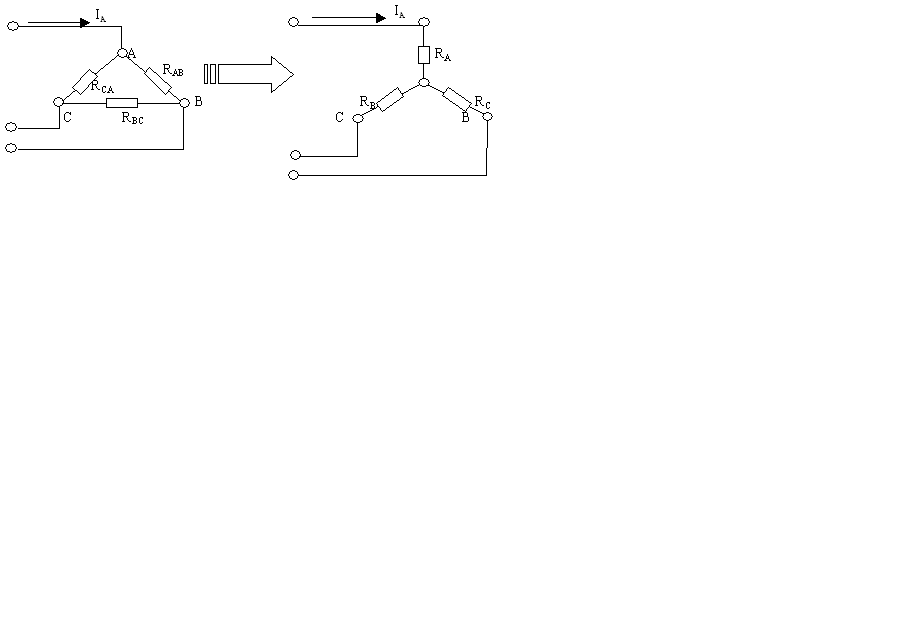
4-сурет

Жұлдызша сұлбаның кедергілерін түрлендірілген үшбұрыш сұлбаның кедергілері арқылы табуға болады: R_A=R_AB ∙R_CA /(R_AB+R_CA+R_BC); R_B=R_AB ∙R_BC /(R_AB+R_CA+R_BC); R_C=R_CA∙R_BC /(R_AB+R_CA+R_BC).

Жұлдызша сұлбаны үшбұрыш сұлбаға түрлендіргенде оның кедергілері төмендегі формулалар арқылы табылады: R_AB=R_A+R_B+R_A∙R_B/R_C; R_BC=R_B+R_C+R_B∙R_C/R_A; R_CA=R_C+R_A+R_C∙R_A/R_B

№ 7 емтихан билеті

1. Индуктивтілік деген не?

2. Теңгеру принципі

3. Суретте көрсетілген электр схемасының параметрлері: U_Л=220 B, R_аб=5 Ом, R_са=6 Ом, х_аб=10 Ом, х_бс=8 Ом, х_са=4 Ом. Осы параметрлер және сызықты кернеу арқылы фазалық тоқтарды және барлық тізбектің жеке бөліктері үшін активті қуатты анықтау керек.

1) Индуктивтілік(лат. іnductіo – келтіру, бейімдеу, қоздыру) – электр тізбегінің магниттік қасиетін сипаттайтын шама. Өткізгіш контурмен шектелген бетті қиып өтетін магниттік индукция ағынының (Ф) осы контурда тудыратын ток күшіне (І) қатынасына тең: L=Ф/І. И. Өлшем бірлігі Генри (Гн). Өзара қатар ораласқан, орам сандардары w₁ және w₂ тең екі индуктивтілік орамалармен i₁ және i ₂ токтары жүрсе, онда әр ораманың барлық магнит сызықтары екінші ораманың орамдарымен ілінісуі мүмкін, яғни Ф₂₁ =Ф₁₁, Ф₁₂ =Ф₂₂. Сондықтан мұндай тізбектерді талдау кезінде орамалардың өздерінің ағын ілінісулерінен ( Ψ₁₁ және Ψ₂₂) басқа қосымша ағын ілінісулерін ( Ψ₁₂ және Ψ₂₁) есепке алу керек. Бірінші ораманың өзіндік ағын ілінісуі Ψ₁₁=Ф₁₁ w₁=L₁ i₁, бірінші ораманың тогының әсерінен пайда болған екінші орамадағы қосымша ағын ілінісуі Ψ₂₁= Ф₂₁ w₂=Ф₁₁ w₂=М₂₁ i₁ , мұндағы М₂₁= Ψ₂₁/i₁ –пропорциональдық коэффициент, өзаралық индуктивтілік деп аталады. Бұл өрнектерден

L₁/ М₂₁= w₁/ w₂.

2)Теңгеру принципі: Тізбектің тармағындағы кедергіні сандық мәні сол кедергі мен токтың көбейтіндісіне тең, ал бағыты токтың бағытына қарама- қарсы электр қозғаушы күшімен айырбастауға болады

№ 8 емтихан билеті

1 . Сыйымдылық деген не?

2. Өзаралық принцип

3. Суретте көрсетілген электр схемасының параметрлері: U_Л=127 B, R_аб=5 Ом, R_СА=6 Ом, х_аб=10 Ом, х_бс=8 Ом, х_са=4 Ом. Осы параметрлер және сызықты кернеу арқылы фазалық тоқтарды, сызықты тоқтарды, барлық тізбектің жеке бөліктері үшін активті қуатты анықтау керек.

1)Сыйымдылық (Емкость; capacity) — 1) компьютер жадына, сақтау құрылғыларына жазуға болатын мәліметтердің ең көп мөлшері (өлшем бірліктері: бит, байт, сөз немесе таңба). Биттермен, байттармен (Кб, Мб, Гб), символдармен немесе сөздермен өлшенеді; 2) байланыс арнасында — мәліметтер жеткізу (өткізу) мүмкіндігі (бір секундта өткізілетін мәліметтер көлемі); 3) машиналық сөздің немесе регистрдің ұзыңдығы.

2) Өзаралық принцип: Тізбектің k тармағына орналасқан э.қ.к. m тармағында I_m (I_m=E_к ∙G_km) тогын тудырса, онда m тармағындағы э.қ.к. Е_m=E_к k тармағында мәні I_m-ге тең I_k (I_к =E_m ∙G_mk )тогын тудырады. G_km , G_mk -өзаралық өткізгіштіктер.

№ 9 емтихан билеті

1. Активті кедергі деген не?

2. Контурлық токтар тәсілі

3. Суретте көрсетілген электр схемасының параметрлері: Е=100 B, f=50 Гц, С₁ =637 мкФ, С₂ =300 мкФ, L₃=15,9 мГн, R₁=8 Ом, R₂=3 Ом, R₃=4 Ом Барлық тізбектің тармақтарындағы тоқтарды, бөліктердің кернеуін, активті, реактивті және толық қуатты табу керек

1) Кедергісі бар элементті резистор дейді. Осы резистордың айнымалы токқа көрсететін кедергісін активті кедергі деп атайды. Активті кедергі айнымалы токтың электр энергиясының жылу энергиясына айналуын сипаттайды.

2) . Бұл тәсілді қолданған кезде электр сұлбасының тәуелсіз контурында тек өзінің контурлық тогы жүреді деп есептейді. Контурлық ток деп қарастырылған контурдың барлық тармақтарымен жүреді деп шартты түрде қабылданған ток. Бұл тәсіл бойынша теңдеулер Кирхгофтың екінші заңы бойынша контурлық токтарға байланысты құрылады. Сондықтан есептеу жұмысы көп жеңілдейді.

Контурлық токтар тәсілінің есептеу жұмысында қолданылуын 6-суретте көрсетілген тізбектің тармақтарындағы токтарды анықтау арқылы қарастырайық. Әрбір контур үшін контурлық токтың бағытын өз қалауымызша, мысалы сағат тілінің жүрісінің бағытымен бағыттас етіп таңдап аламыз. Екі контурға ортақ тармақпен жүретін контурлық токтар бағыттас болса, онда олардың қосындысы алынады. Керісінше жағдайда олардың айырмасын алады. Жалпы жағдайда қарастыралатын тізбек үшін теңдеулер мынадай түрде жазылады:

Е₁₁= I₁₁∙R₁₁+ I₂₂∙R ₁₂ + I ₃₃∙ R ₁₃

Е₂₂= I₁₁∙R₂₁+ I₂₂∙R ₂₂ + I ₃₃∙ R ₂₃

Е₃₃= I₁₁∙R₃₁+ I₂₂∙R ₃₂ + I ₃₃∙ R ₃₃

Мұндағы Е₁₁, Е₂₂, Е₃₃- бірінші, екінші және үшінші контурлардың контурлық э.қ.к.-тері;

R₁₁, R₂₂, R ₃₃- бірінші, екінші және үшінші контурлардың өзіндік кедергілері,

R₁₁= R₁+R₅ +R₃; R₂₂= R₂+R₄+R₅; R ₃₃= R₆+R₄ +R₃.

R ₁₂=R₂₁- бірінші мен екінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

R₁₃= R₃₁- бірінші мен үшінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

R ₂₃= R ₃₂- екінші мен үшінші контурларға ортақ тармақтың кедергісі, “минус” таңбасымен алынады.

Теңдеулер 6-суретте көрсетілген тізбек үшін былай жазылады:

E₁ – E₃=I₁₁∙(R₁+R₅ +R₃) – I₂₂∙R₅ –I₃₃∙R₃

– E₂+E₄= I₂₂∙ (R₂+R₄+R₅) – I₃₃∙R₄ –I₁₁∙R₅

E₃ – E₄=I₃₃∙ (R₆+R₄ +R₃) – I₁₁∙R₃– I₂₂∙R₄

Әр теңдеудегі жақшаның ішінде кедергілердің қосындысы контурдың өзіндік кедергісі деп аталады. Теңдеулер жүйесін шешеміз де I_11, I_22, I₃₃ контурлық токтарын табамыз. Тармақтардың токтарын (I₁ ... I₆) контурлық токтар арқылы табамыз:I₁=I₁₁, I₂= –I ₂₂, I₃= I₃₃ – I₁₁, I₄=I₂₂–I₃₃, I₅=I₁₁ – I₂₂, I₆= –I₃₃

№ 10 емтихан билеті

1. Потенциалдық диаграмма

2. Электр тізбегінің сұлбасы

3. Суретте көрсетілген электр схемасының параметрлері: U_Л=220 B, R_а=3 Ом, R_б=4 Ом, R_с=6 Ом, х_а=4 Ом, х_б=3 Ом, х_с=8 Ом. Осы параметрлер және сызықты кернеу арқылы фазалық тоқтарды және бейтарап тізбектегі (төрт тізбекті схема үшін) сызықты тоқтарды, барлық тізбектің жеке бөліктері үшін активті қуатты анықтау керек.

1) Потенциалдық диаграмма потенциалдың тізбектің өн бойындағы өзгерісін сипаттайды. Тізбектің бір нүктесінің потенциалын нөлге тең деп алады да, қалған нүктелердің потенциалдарын осы нүктенің потенциалымен салыстыра отырып анықтайды. Абцисса осіне масштаб бойынша кедергілерді салады, ал ордината осінде потенциалдарды көрсетеді.

2) Электр тізбегінің сұлбасы деп тізбектің элементтерін және олардың өзара жалғану ерекшеліктерін шартты түрде графикалық жолмен бейнелеуді айтады. Эскиздік сұлбада тізбек элементтері эскиз (сұлба) түрінде көрсетіледі. Бұл сұлбаны қолданған өте ыңғайсыз. Принципиалды электрлік сұлбада тізбектің элементтері ГОСТ бойынша қабылданған арнаулы шартты белгі арқылы көрсетіледі. Бұл сұлба арқылы тізбектің элементтерінің атқаратын қызметін, өзара жалғану жолдарын түсінуге болады, бірақ тізбекті есептеуге мүмкіндік бермейді. Орынбасу сұлбасында электр қондырғысында болып жатқан электромагниттік құбылыстарды зерттеуге мүмкіндік беретін идеал элементтермен (сыйымдылық элемент, кедергі, индуктивтілік элемент) айырбастаймыз Кедергі электр энергиясының жылу энергиясына айналу құбылысын сипаттайды. Индуктивті элемент электр энергиясының магнит энергиясына айналу құбылысын сипаттайды. Сыйымдылық элемент электр энергиясының электр өрісінің энергиясына айналу құбылысын сипаттайды.

№ 11 емтихан билеті

1. Активті қуат

2. Түйіндік потенциалдар тәсілі

3. Суретте көрсетілген схемадағы А Б О Ж К Л А контуры үшін Кирхгофтың екінші заңы бойынша теңдеу құрастыр.

1) Активті лездік қуат p_a=U_aI – U_aIcos2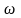 t= UIcos - UIcos cos2 t, яғни ол тұрақты құраушыдан және айнымалы құраушыдан тұрады. Айнымалы құраушы екі еселенген жиілікпен өзгеретін, амлитудасы UIcos -ге тең косинусоида болады. Лездік қуаттың бір период ішіндегі орташа мәні активті қуат деп аталады. Ол лездік қуаттың тұрақты құраушысына тең: P= UI cos = u_aI= rI².

2) Сұлбалардағы түйіндердің потенциалдарын белгісіз ретінде қабылдап, электр тізбектерін есептеу тәсілін түйіндік потенциалдар тәсілі деп атайды.Айталық, сұлбада n-түйін болсын. Сұлбаның кез-келген бір нүктесін ойша жермен қосамыз, яғни оның потенциалын нөлге тең деп аламыз.Соның нәтижесінде белгісіздер саны n-1-ге дейін азаяды. Бұл тәсіл бойынша теңдеулер Кирхгофтың бірінші заңы бойынша түйінде түйіскен токтарға арнап құрылады. Токтарды түйіндердің потенциалдары арқылы Ом заңы бойынша өрнектеуге болады. Нәтижесінде теңдеулер жүйесі мынадай түрде жазылады:

φ₁G₁₁ + φ₂G₁₂ + φ₃G₁₃= I₁₁

φ₁G₂₁ + φ₂G₂₂ + φ₃G₂₃= I₂₂

φ₁G₃₁ + φ₂G₃₂ + φ₃G₃₃= I₃₃

φ₁, φ₂, φ₃- бірінші, екінші және үшінші түйіндердің потенциалдары; G₁₁, G₂₂, G₃₃-- бірінші, екінші және үшінші түйіндерде түйіскен тармақтардың өткізгіштердің қосындысы; G_km- k мен m түйіндерді байланыстыратын тармақтың өткізгіштігі, “минус” таңбасымен алынады; I₁₁, I₂₂, I₃₃- түйіндердің түйіндік токтары. Белгілі бір түйіннің түйіндік тогы сол түйінмен байланысқан тармақтардағы э.қ.к.-терді сол тармақтардың кедергілеріне бөлу арқылы табылған токтардың алгебралық қосындысына тең. Э.қ.к.-тері түйінге бағытталған тармақтардың токтары «плюс» таңбасымен алынады, ал керісінше жағдайда «минус»таңбасы алынады.

Берілген тізбектің (6-сурет) « г» түйінінің потенциалын нөлге тең деп аламыз.Теңдеулер көрсетілген тізбек үшін былай жазылады:

φ_а(g₁+g₃+g₆) - φ_бg₁ - φ_вg₆= -E₁g₁-Е₃g₃

φ_б(g₁+g₂+g₅) - φ_аg₁ - φ_вg₂= E₁g₁ + E₂g₂

φ_в(g₂+g₄+g₆) - φ_бg₂ - φ_аg₆= -E₂g₂ -E₄g₄

Мұндағы g₁=1/R ₁, g₂=1/R₂, g₃=1/R₃ , g₄=1/R₄ , g₅=1/R₅ , g₆=1/R₆.

Теңдеулер жүйесін шешу арқылы φ_а, φ_б, φ_в табамыз. Токтардың мәндерін Ом заңы арқылы табамыз:

I₁= (E₁+ U_аб)/R₁ = [E₁+(φ_а - φ_б)]/R₁, I₂= (E₂+ U_вб)/R₂=[E₂+(φ_в- φ_б) ]/R₂, I₃= (E₃+ U_аг)/R₃=[E₃+ (φ_а - φ_г) ]/R₂

I₄= U_вг/R₄=(φ_в - φ_г)/R₄ = φ_в/R₄ I₅= U_бг/R₅=(φ_б - φ_г)/R₄ = φ_б/R₅ I₆= (E₆+ U_ав)/R₆=[ E₆+ (φ_а - φ_в) ]/R₆

№ 12 емтихан билеті

1. Толық қуат

2. Электр сұлбаларының топологиялық элементтері

3. Суретте көрсетілген электр схемасының параметрлері: Е=150 B, f=50 Гц, С₁ =637 мкФ, С₂ =300 мкФ, L₃=15,9 мГн, R₁=2 Ом, R₂=3 Ом, R₃=4 Ом Барлық тізбектің тармақтарындағы тоқтарды, бөліктердің кернеуін, активті, реактивті және толық қуатты табу керек.

1) . Айнымалы құраушының амплитудасы UI тұрақты құраушыдан артық болғандықтан лездік қуат кейбір сәттерде теріс таңбалы болады. Бұл кезде тізбек қоректендіргішке энергияны қайтып береді. Қайтарылатын энергия тізбектің реактивті бөлігінің энергиясының есебінен жүреді. Айнымалы бөліктің амплитудасын S деп белгілейміз де, толық қуат деп атаймыз: S= IU. Өлшем бірлігі- вольтампер [ВА].

2) Электр сұлбаларының топологиялық элементтері. Тармақ деп элементтері бір-бірімен бірізді жалғанған, бойымен бір ғана тоқ жүретін тізбек бөлігін айтамыз. Түйін деп кем дегенде үш тармақтың түйіскен нүктесін айтады. Контур деп бірнеше тармақ арқылы өтетін тізбектің тұйық бөлігін айтады.

№ 13 емтихан билеті

1. Реактивті қуат

2. Екі түйіндік тәсіл

3. Суретте көрсетілген электр схемасының параметрлері: U_Л=380 B, R_аб=5 Ом, R_са=6 Ом, х_аб=10 Ом, х_бс=8 Ом, х_са=4 Ом. Осы параметрлер және сызықты кернеу арқылы фазалық тоқтарды және барлық тізбектің жеке бөліктері үшін активті қуатты анықтау керек.

1) Лездік реактивті қуаттың амплитудасын (UIsin ) реактивті қуат Q_p= UIsin деп атайды. Өлшем бірлігі- вольтампер реактивтік [ВАр]. Q_p= Q_L – Q_C= x_LI² – x_CI²= U_LI – U_C I =U_p I.

2) Көп жағдайда екі түйіннен тұратын электр сұлбалар кездеседі. Мұндай сұлбаларды есептеу үшін түйіндік потенциалдар тәсілінің жеке бір түрі –екі түйіндік тәсілді қолданған тиімді. Бұл тәсіл бойынша екі түйін арасындағы кернеуді табу арқылы тармақтардағы токтарды анықтайды. Мысалы, 7-суреттегі тізбектің тармақтарындағы токтарды табайық. Ол үшін алдымен U_аб кернеуін табамыз. Тізбектің «б » түйінінің потенциалын нөлге тең деп аламыз. Сонда U_аб=φ_а – φ_б = φ_а – 0 = φ_а.

Тізбектің «а » түйіні үшін: I₁ + I₂ +I₃ + I₄=0,

мұндағы I₁= (E₁ - U_аб)/R₁=(E₁-φ_а)/R₁,

I₂= - U_аб . R₂= -φ_а . R₂, I₃= (-E₃ - U_аб).R ₃=(-E₃-φ_а).R₃, I₄= -φ_а . R₄.

Токтардың өрнектерін теңдеуге қоямыз да , φ_а табамыз:

φ_а(g₁+g₂+g₃+g₄)= E₁g₁ – E₃g₃,

φ_а=(E₁g₁ – E₃g₆)/ (g₁+g₂+g₃+g₄).

Табылған φ_а мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Табылған φ_а мәнін токтардың өрнектеріне қойып, олардың мәндерін анықтаймыз. Жалпы жағдайда U_аб =∑ E_кg_к /∑g_к.