
- •Билет 16. Показатели безотказности невосстанавливаемых систем
- •Алгоритм топологического метода расчета надежности.(Топологический метод расчета надежности)
- •Определитель графа
- •Билет 17. Показатели безотказности восстанавливаемых систем
- •Идея топологического метода расчета надежности систем.
- •Билет 18. Показатели сохраняемости
- •Надежность программного обеспечения информационных систем.
- •Билет 20. Показатели долговечности
- •Резервирование методом динамического программирования.
- •Белет 21. Комплексные показатели надежности
- •Билет 23. Классификация отказов информационных систем
- •Билет 24. Понятие и свойства надежности
- •Одновыборочный контроль надежности.
- •Билет 25. Алгоритм топологического метода расчета надежности.(Топологический метод расчета надежности)
- •Определитель графа
- •Билет 26. Классический метод расчета надежности систем
- •Статистическая оценка показателей надежности при определительных испытаниях
- •Билет 28 Методы контроля надежности массовой продукции.
- •Классификация отказов информационных систем
- •Билет 29. Показатели безотказности восстанавливаемых систем
- •Одновыборочный контроль надежности.
- •Билет 30. Основные понятия и определения теории надежности.
- •Методы и виды резервирования.
Билет 20. Показатели долговечности
В качестве случайных величин, характеризующих долговечность технических систем, применяют две:
-ресурс - наработка системы до списания выраженная во временных единицах измерения без учета простоев;
-срок службы - календарная продолжительность службы объекта до его списания.
Считаются известными законы распределения случайной величины ресурса fр(t) и Fр(t) или случайной величины срок службы fсл(t) и Fсл(t). Рассмотрим наиболее употребимые показатели долговечности.
1) Средний ресурс или средний срок службы – математическое ожидание средней величины ресурса или срока службы совокупности изделий одного типа и исполнения:
 ,
,
 .
.
2) Гамма-процентный ресурс или срок службы, который имеют и превышают в среднем определенное число - процентов изделий Tрg, Tслg:
 ,
,
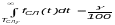 .
.
3) Медианный ресурс или срок службы Трм, Тслм:
 ,
,
 .
.
Резервирование методом динамического программирования.
Для решения задачи оптимального резервирования также используется метод динамического программирования.
Рассмотрим алгоритм решения поставленной задачи методом динамического программирования. В основе метода лежит пошаговый процесс, на каждом шаге строится доминирующая последовательность

где переход в состояние с более высокой надежностью (или более низкой вероятностью отказа Q) происходит с минимальными затратами по стоимости C,
здесь

- риск нехватки резервных элементов.
Доминирующая последовательность строится по следующему правилу

Алгоритм построения доминирующей последовательности состоит из шагов, на каждом из которых строится следующая таблица.
Рассматриваем две подсистемы из 1-го и 2-го типа элементов. Характеристики элементов 1-го типа записываются в заголовках столбцов, а характеристики 2-го типа - в заголовках строк. На пересечении каждой строки и каждого столбца записываются суммы стоимостей C и вероятностей нехватки элементов q.
Таблица 1.

Вначале проводим анализ элементов таблицы по ограничениям . Вычеркиваем те элементы, которые имеют значение стоимости большее, чем ограничение по стоимости Co и, чем ограничение по вероятности нехватки элементов Qo.
Делаем анализ на доминирование: рассматриваются оставшиеся клетки и сравниваем последовательно со всеми элементами (клетками). Если для каких-то двух векторов выполняется условие строгого доминирования, то т худший вычеркивается.
Вектор X1 доминирует над вектором X2, если вероятность нехватки элементов

или вероятность нехватки элементов

Вектор X1 строго доминирует над вектором X2, если одно из перечисленных неравенств будет строгим.
Все оставшиеся элементы переносим в заголовки столбцов, а в качестве заголовков строк будут выступать характеристики элементов третьего типа.
Всего будет S-1 таблица, на последнем шаге вычислений ищется оптимальный вектор, у которого и будет минимальная вероятность отсутствия резервных элементов.
Белет 21. Комплексные показатели надежности
Показатели, зависящие более чем от одного свойства, называются комплексными. Чаще всего комплексные показатели отражают два свойства надежности: безотказность и ремонтопригодность. К таким показателям относятся:
- функции готовности и простоя;
- коэффициенты готовности и простоя;
- коэффициент технического использования;
- коэффициент оперативной готовности.
Чаще
всего комплексные показатели отражают
два свойства надежности: безотказность
и ремонтопригодность. К таким показателям
относятся: функции готовности и простоя;
коэффициенты готовности и простоя;
коэффициент технического использования;
коэффициент оперативной готовности.
Функция готовности Кг(t) -
вероятность того, что в любой произвольный
момент времени система будет находиться
в работоспособном состоянии. Функция
простоя Кп(t) - вероятность того,
что в произвольный момент времени
система будет находиться в неработоспособном
состоянии: Кп(t) = 1 - Кг(t).
 ,
,

 .
Коэффициент готовности можно определить
по статистическим данным:
.
Коэффициент готовности можно определить
по статистическим данным:
где ti - наработка
на отказ; i -
время восстановления после i-го отказа;
n - число отказов за рассматриваемый
период. Если разделить числитель и
знаменатель правой части на n, то получим
 При n:
При n:
 Коэффициент простоя: Кп(t) = 1 -
Кг(t)=1-
Коэффициент простоя: Кп(t) = 1 -
Кг(t)=1-
 =
=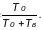
 .
Коэф-т готовности – вер-ть застать
сист.в произвол.мом.вр.в работосп.сост.,кроме
планов.застоев,когда сист.не примен.по
назнач. Коэффициент технического
использования - отношение
математического ожидания нахождения
системы в работоспособном состоянии к
сумме математических ожиданий нахождения
системы в работоспособном состоянии и
в неработоспособном с учетом плановых
и неплановых перерывов.
.
Коэф-т готовности – вер-ть застать
сист.в произвол.мом.вр.в работосп.сост.,кроме
планов.застоев,когда сист.не примен.по
назнач. Коэффициент технического
использования - отношение
математического ожидания нахождения
системы в работоспособном состоянии к
сумме математических ожиданий нахождения
системы в работоспособном состоянии и
в неработоспособном с учетом плановых
и неплановых перерывов.
 .где
tпi - время планового простоя, tнi
- время непланового. Коэффициент
оперативной готовности:
.где
tпi - время планового простоя, tнi
- время непланового. Коэффициент
оперативной готовности:
 .
Коэффициент оперативной готовности
определяет вероятность безотказного
функционирования системы при выполнении
ожидаемой задачи. Ког – вероятность
того, что система окажется в работоспособном
состоянии в произвольный момент времени,
кроме планируемых периодов, в течении
которых применение системы по назначению
не предусматривается, и, начиная с этого
момента будет работать безотказно в
течение заданного интервала времени
tог.
.
Коэффициент оперативной готовности
определяет вероятность безотказного
функционирования системы при выполнении
ожидаемой задачи. Ког – вероятность
того, что система окажется в работоспособном
состоянии в произвольный момент времени,
кроме планируемых периодов, в течении
которых применение системы по назначению
не предусматривается, и, начиная с этого
момента будет работать безотказно в
течение заданного интервала времени
tог.
Контроль надежности методом двухкратной выборки.
В
планах типа двукратной выборки из
общего числа изделий N выбирается n1
изделий (n1 > N). Эта выборка
подвергается контролю на надежность и
подсчитывается число дефектных изделий
в n1. Если d(n1) ≤ c1, то
партия принимается, d(n1) > c2
– партия бракуется. c1 < d(n1)
≤ c2 – зона неопределенности.
Берется вторая выборка n2, такая,
что (n1 + n2 < N) и подвергается
контролю на надежность. Если d(n1
+ n2) ≤ c3 – партия принимается,
d(n1 + n2) > c3 – партия
бракуется. Возможен вариант, когда c2
= c3.Оперативная характеристика
П(q) = Ра1 + Ра2, где Ра1
и Ра2 –несовместимые события.
Событие а1: d(n1) < c1;
а2: d(n1 + n2) ≤ c2;
d(n1) > c1. Партия изделий
будет принята, если наступит одно из
несовместных событий:– а1: для
первой выборки выполняется условие
 ;
– а2: для двух последних выборок
выполняются условия
;
– а2: для двух последних выборок
выполняются условия
 ,
,
 Тогда
оперативная характеристика
Тогда
оперативная характеристика
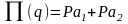 ,
где Ра1 – вероятность события а1,
Ра2 – вероятность события а2.
,
где Ра1 – вероятность события а1,
Ра2 – вероятность события а2.

БИЛЕТ 22. Последовательный контроль надежности.
При
последовательном контроле надежности
берется целый ряд выборок и каждый раз
сравнивается с приемочными числами.
Необходимо, чтобы было соблюдено условие
(n1 + n2+…+ni) ≤ N. . Если
d(n1 + n2+…+ni) = di.
Тогда возмём выборку n1, подсчитаем
d(n1) и сравним с передаточными
числами. Если d1 ≤ c1 – партия
принимается, d1 > c1’ –
партия бракуется. c1 < d(n1)
≤ c1’ – зона неопределенности.
Необходимо взять выборку n2 и
подсчитать d2. Если d2 ≤ c2
– партия принимается, d2 > c2’
– партия бракуется. c1 < d(n1)
< c2’ – зона неопределенности.
Последовательный контроль надежности
проводится по накопленному числу
дефектных изделий r = 1, 2, 3,… или по
суммарной наработке на отказ Т∑r
в зависимости от плана испытаний. В
основе принятия решений лежит вероятность
gr – отношение
правдоподобия, r = 1,2,3,… которая и
сравнивается с величинами риска
поставщика и потребителя. Если ,
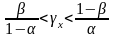 –
продолжается испытание,
–
продолжается испытание,
 – партия принимается,
– партия принимается, –
партия бракуется.
–
партия бракуется.
Коэффициент технического использования - отношение математического ожидания нахождения системы в работоспособном состоянии к сумме математических ожиданий нахождения системы в работоспособном состоянии и в неработоспособном с учетом плановых и неплановых перерывов.
 .
.
где tпi - время планового простоя, tнi - время непланового.
