Идея топологического метода расчета надежности систем.

Использ.теория графов и ввод.услов.обознач. Обозначим Х как множество состояний системы: , где xi – i-е состояние, I – множество индексов всех возможных состояний системы, n – количество возможных состояний системы.

Разобьем множество Х на два подмножества: 1) подмножество работоспособных состояний системы Х_р; , где X_р – подмножество работоспособных состояний системы, I_р – множество индексов работоспособных состояний системы. 2) подмножество неработоспособных состояний системы 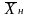. . Представим X(t) в виде вероятностного графа состояний G(X, W), где Х – множество вершин графа, соответствующих множеству состояний X; W – множество дуг, соединяющих вершины данного графа; P₁(t), ..., P_i(t), ..., P₆(t) – вероятности нахождения системы в i-м состоянии; d(w_ij) – вес дуги w_ij; a_ij – интенсивность перехода из состояния i в состояние j. Если заданы интенсивности a_ij, то, составляя и решая систему уравнений Колмогорова, можно определить вероятности нахождения системы в i-м состоянии P_i(t), а значит и показатели надежности. Однако составление и решение системы уравнений Колмогорова является трудоемкой операцией, поэтому для решения подобных задач применяют топологический метод.

Билет 18. Показатели сохраняемости

Определение свойств сохраняемости аналогично определению свойств безотказности с тем лишь различием, что они относятся к разным условиям: свойство безотказности характеризует рабочие эксплуатационные условия, а свойство сохраняемости – нерабочие условия (хранение и транспортировка). Показатели сохраняемости аналогичны показателям безотказности. Однако вычислять их нужно не через функции f_н(t) и Q(t), а через законы распределения длительности безотказного хранения f_хр(t) и F_хр(t).

Срок сохраняемости – календарная продолжительность хранения или транспортировки изделия, в течение и после которой сохраняются значения показателей безотказности, долговечности и ремонтопригодности в установленных пределах.

Из всего множества показателей сохраняемости наиболее часто в технической документации используют только два: средний срок сохраняемости и гамма-процентный срок сохраняемости.

Средний срок сохраняемости — математическое ожидание случайной величины хранения до отказа: .

Гамма-процентный срок сохраняемости — срок сохраняемости, который достигается объектом с вероятностью g выраженной в процентах T_хр.:

.

Рекомендуются значения  = 90; 95 и 98%. Кроме того, применяют еще и медианный срок сохраняемости при  = 50% T_хрμ:

.

Надежность программного обеспечения информационных систем.

Показ.надеж.програм.испыт.выявлюпри спец.испыт. Проблемы:необх.определ.понятия; сбои, ошибки в ПО; определ.факторов,от кот.завис.надеж.ПО. Тестир.ПО на стадии их отладки (разраб.тестов и эталонов, на основ.кот.сост.отладоч.задачи, по кот.произв.исполн.и в рез-те приним.реш. удвл.или нет. 1Начало-2планиров-е -3сост-е тесктов- 4состав-е задач- 5трансляц-я задач- 6исполн. прогр-6регистр-я результ-в исп прогр -7результ равен эталону(если =-регистрация завершена),(есди не равен)- 8анализ ошибок- 9можно ли выявить ошибку(если нет,то планирую-я дополнительн-е отладки), (если да)-10планир- 11исправляют…..

БИЛЕТ 19.Показатели ремонтопригодности

Свойство ремонтопригодности в принципе можно определять, как и все остальные свойства надежности, через соответствующие показатели, которые определяются через законы распределения длительности восстановления f_в(t) и F_в(t).

Из всей номенклатуры предлагаемых показателей для характеристики свойства ремонтопригодности применяют следующие:

-интенсивность восстановления

.

-среднее время восстановления

.

-и вероятность восстановления за заданное время

.

Постановка задачи оптимального резервирования.

Информационные системы состоят из отдельных элементов. Эти элементы с течением времени отказывают и заменяются резервными. Снятые с эксплуатации элементы подвергаются ремонту.

Модель должна определять оптимальный уровень резервных элементов каждого типа. По условию задачи требуется, чтобы система функционировала с максимальной надежностью. Если какой-нибудь элемент отказывает, то его заменяют запасным из числа резервных. Отказавший элемент сразу начинают ремонтировать. В системе непрерывно должно функционировать ZK элементов K-го типа, причем в запасе должно иметься XK элементов того же K-го типа

.

Сущность задачи заключается в оптимальном распределении стоимостных или каких-либо других ресурсов , выделенных на приобретение резервных единиц.

Рассматриваемая система считается отказавшей, если в момент отказа работающего элемента K-го типа все XK запасных элементов того же типа находятся в ремонте. Таким образом, надо найти количество резервных элементов

так, чтобы вероятность нехватки резервных элементов была минимальной.

Введем обозначения:

- показатель надежности всей системы (вероятность безотказной работы системы);

- вероятность безотказной работы K-го элемента.

Так как модель соединений элементов с точки зрения надежности представляется как последовательное соединение элементов, то справедлива формула

Можно сформулировать задачу на минимум: необходимо найти минимум риска нехватки элементов

На все элементы есть ограничения (вес, цена, объем и т.д.). Но мы будем пользоваться только стоимостным ограничением, как, пожалуй, наиболее часто встречающимся, хотя задача решается и для нескольких ограничений.

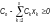
где

- стоимость одного элемента k-го типа.