
- •Билет 16. Показатели безотказности невосстанавливаемых систем
- •Алгоритм топологического метода расчета надежности.(Топологический метод расчета надежности)
- •Определитель графа
- •Билет 17. Показатели безотказности восстанавливаемых систем
- •Идея топологического метода расчета надежности систем.
- •Билет 18. Показатели сохраняемости
- •Надежность программного обеспечения информационных систем.
- •Билет 20. Показатели долговечности
- •Резервирование методом динамического программирования.
- •Белет 21. Комплексные показатели надежности
- •Билет 23. Классификация отказов информационных систем
- •Билет 24. Понятие и свойства надежности
- •Одновыборочный контроль надежности.
- •Билет 25. Алгоритм топологического метода расчета надежности.(Топологический метод расчета надежности)
- •Определитель графа
- •Билет 26. Классический метод расчета надежности систем
- •Статистическая оценка показателей надежности при определительных испытаниях
- •Билет 28 Методы контроля надежности массовой продукции.
- •Классификация отказов информационных систем
- •Билет 29. Показатели безотказности восстанавливаемых систем
- •Одновыборочный контроль надежности.
- •Билет 30. Основные понятия и определения теории надежности.
- •Методы и виды резервирования.
Классификация отказов информационных систем
Во многих случаях понятие отказа удобно подразделять на его виды в соответствии с классификационными признаками:
1)По характеру возникновения:
- Внезапные (катастрофические). Возникают в результате резкого (скачкообразного) изменения выходных показателей системы;
-Постепенные (параметрические). Образуются при постепенном снижении выходных параметров системы во времени и когда эти параметры пересекают критическое значение, считается, что отказ произошел.
2)По степени очевидности:
- Явные (очевидные). Явные отказы системы обнаруживаются при внешнем осмотре или включении системы;
- Скрытые (неочевидные). Выявляются инструментальными средствами.
3)По связи с отказами других элементов:
- Зависимые (вторичные отказы). Возникают под влиянием отказов других элементов;
- Независимые (первичные отказы).
4) По времени существования:
- Устойчивые (окончательные). Устраняются только в результате ремонта;
- Перемежающие отказы (самопроизвольно возникают и устраняются). Исчезают без вмешательства обслуживающего персонала (например, сбои ЭВМ).
5)По влиянию на ремонтопригодность:
- Неисправности. Устраняются путем мелкого ремонта;
- Аварии. Требуют длительного восстановления и больших ремонтных работ.
6)По природе возникновения:
- Физические. Проявляются в физическом нарушении работоспособности;
- Функциональные. Теряют способность системы выполнять некоторые или все функции (например, при отсутствии физического отказа ЭВМ может неправильно выполнять логические операции).
Билет 29. Показатели безотказности восстанавливаемых систем
Восстанавливаемые системы имеют поток отказов и периодически подвергаются воздействию системы технического обслуживания и ремонта. (рис.1.9), где
Процесс эксплуатации
ti — i-ая наработка на отказ.
ti — i-ое время восстановления после i-ого отказа
Случайную величину длительности безотказной работы между соседними периодами восстановления системы можно характеризовать функцией распределения длительности безотказной работы между окончанием восстановления после (i-1)-го отказа и моментом наступления i-го отказа Fi(t). Тогда показатель Qi(t) = Fi(t) будет означать вероятность наступления отказа системы за промежуток времени t после окончания (i-1)-го восстановления. Вероятность безотказной работы с момента окончания (i-1)-го восстановления за период t:
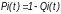 .
.
![]() .
.
Средняя наработка на отказ за интервал времени от момента окончания (i-1)-го восстановления до наступления i-го отказа: Toi
Перечисленные
показатели можно назвать локальными.
Они характеризуют безотказность в
интервалах времени между двумя соседними
отказами. Частным случаем локальных
показателей безотказности восстанавливаемых
систем будут показатели безотказности
невосстанавливаемых систем, если
рассматривать свойства безотказности
до первого отказа


![]()
и т.д.
Для общего случая, который учитывает все отказы за интервал времени t, используются общие показатели безотказности, в частности ведущая функция потока отказов
![]()
(математическое ожидание случайного числа отказов за время t):
![]()
где М – математическое ожидание;
N(t) – случайное число отказов.
Следующий общий показатель безотказности - параметр потока отказов (среднее значение количества отказов в единицу времени за рассматриваемый интервал времени - имеет вид
 .
.
Справедливо обратное соотношение
 .
.
Наглядной характеристикой восстанавливаемых систем является среднее значение параметра потока отказов за рассматриваемую наработку TP:

Среднюю наработку между отказами восстанавливаемого изделия характеризует показатель Т:

Предел параметра потока отказов
 .
.
Показатель (t):
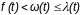 .
.
Если случайные величины наработки между отказами одинаково распределены и независимы (одинаковые законы распределения случайной величины наработки между отказами), т.е. F1(t) = F2(t) = … = Fk(t), то
![]()
связан с плотностью распределения наработки между отказами f(t) уравнением возобновления
![]()
В некоторых случаях удобно искать решение преобразованием Лапласа:

Где
 .
.
Если функция распределения наработки между отказами подчиняется экспоненциальному закону распределения, то расчет значительно упрощается.
