
- •Математическое моделирование управляемых динамических систем
- •1.Уравнения газореактивной системы управления движением спутника с упругим стержнем и закрепленным на его конце телом.
- •2. Асимптотические разложения по методу многих масштабов.
- •3. Решение уравнений нулевого приближения программного поворота спутника относительно орбитальной системы координат при наличии постоянного возмущающего момента внешних сил
- •4. Решение уравнений первого приближения движения спутника относительно состояний подвижного равновесия нулевого приближения.
- •5. Динамическое моделирование системы угловой стабилизации спутника с упругим стержнем и закрепленным на его конце телом по типовым логарифмическим частным характеристикам
- •6. Динамическое моделирование программного поворота спутника с упругим стержнем и закрепленным на его конце телом относительно орбитальной системы координат.
- •7. Математическое моделирование программного поворота упругого звена манипулятора.
- •7.1. Уравнение движения упругого звена манипулятора
- •Список используемой литературы:
7. Математическое моделирование программного поворота упругого звена манипулятора.
Рассмотрим задачу об управлении плоским угловым движением упругого звена манипулятора [1],[12] с вязкоупругим стержнем, внутреннее трение в котором учитывается по теории Фойгта.
7.1. Уравнение движения упругого звена манипулятора
Рассмотрим применительно к манипуляторам задачу об управлении плоским угловым движением дискретно-континуальной механической модели (рис. 4) с упругим стержнем, внутреннее трение в котором учитывается по теории Фойгта.
Рис.
4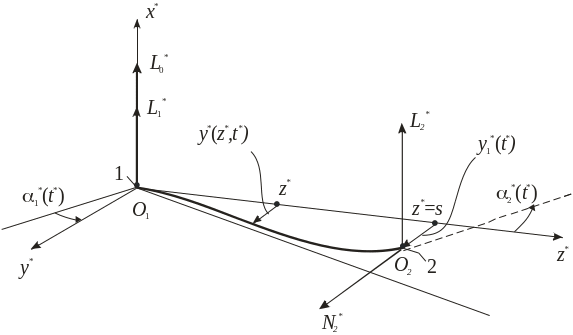
![]() ,
,
где 0* - задаваемый угол (входная функция);
1* - угол поворота тела 1;
П – оператор корректирующего устройства;
р* - коэффициент усиления;
k
![]()
точка означает дифференцирование по времени t*
Учитывая малость деформации стержня, запишем полярный угол *(t*) выходной точки О2 гибкого стержня в виде :
![]() ,
,
где s – длина стержня. Причем |y*(s,t*)|=|y1*(t*)|<<s и |y*(z*,t*)|<<s для z*[0, s].
Обозначим через L1*, L2*, N2* реакции стержня соответственно: моменты сил (L1*, L2*) и сила (N2*), приложенные к абсолютно жестким телам.
Уравнения движения КДС запишем, следуя механике Ньютона-Эйлера
![]() ОДУ
ОДУ
![]()
![]() УЧП
УЧП
![]() ГУ
ГУ
![]()
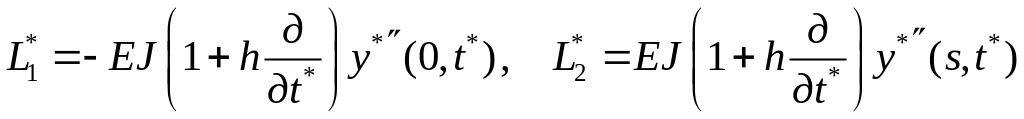 УС
УС
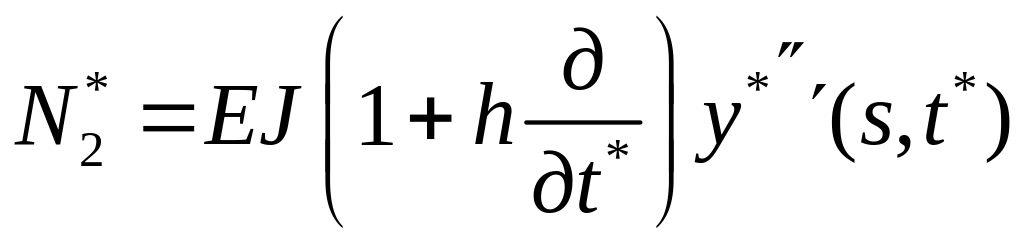
![]() НУ
НУ
![]()
где 0*(t*) – входная функция, *(t*) – выходная функция, - погонная плотность стержня, Е – модуль упругости (Юнга), J – экваториальный момент инерции поперечного сечения стержня, h – коэффициент внутреннего трения стержня по Фойгту.
Обозначим через характерный прогиб стержня и введем безразмерные переменные и параметры:
 -
характерное время протекающих в системе
процессов, t – безразмерное время;
-
характерное время протекающих в системе
процессов, t – безразмерное время;
![]() ,
y1-
безразмерное упругое перемещение конца
стержня;
,
y1-
безразмерное упругое перемещение конца
стержня;
y*=y, y – безразмерный прогиб стержня;
z*=sz, z – безразмерная координата поперечного сечения стержня.
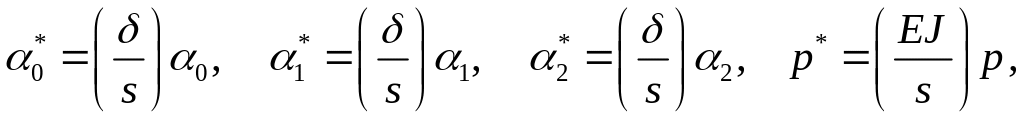
![]() ,
,
![]()
![]()
Здесь 0, 1, 2, p, J0, J1, J2, m2 , k0, L1, L2, N2, – безразмерные значения соответствующих размерных переменных и параметров.
Перепишем уравнения движения КДС в безразмерной форме
![]() ОДУ
ОДУ
![]()
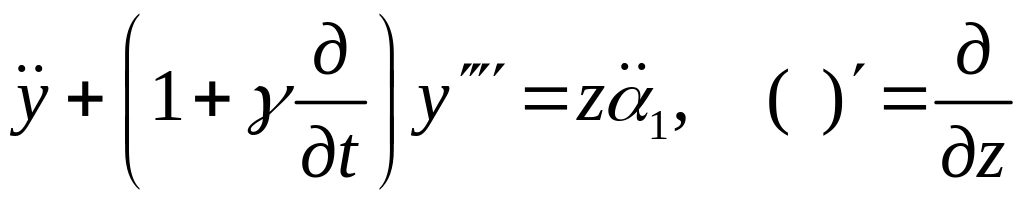 УЧП
УЧП
![]() ГУ
ГУ
![]()
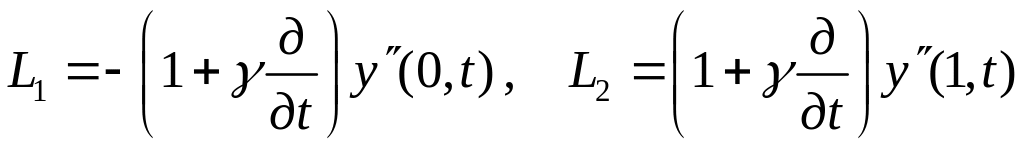 УС
УС
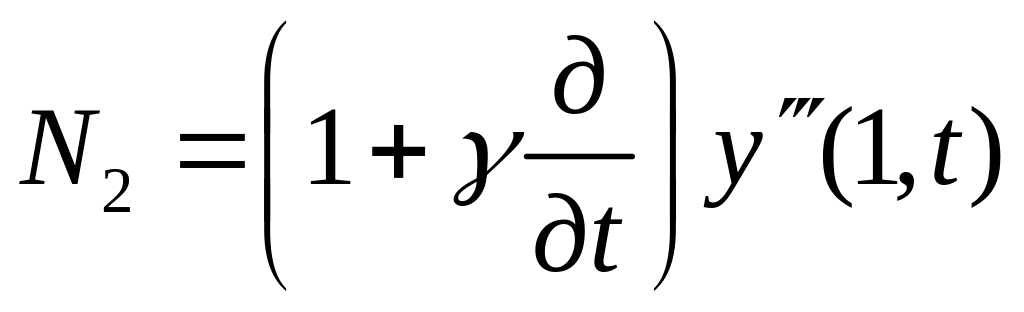
![]() НУ
НУ
![]()
Обозначая
малый параметр задачи
![]() вводя быстрое время
вводя быстрое время
![]() и медленное время
и медленное время
![]() ,
полагаем входную функцию в форме
,
полагаем входную функцию в форме
![]()
Следуя методу многих масштабов, представляем реакции рассматриваемой динамической системы в виде асимптотических разложений

Повторяя
приведенные в предыдущих разделах
рассуждения, получаем уравнение нулевого
приближения полярного угла
![]() программного движения выходной точки
программного движения выходной точки
![]() упругого звена манипулятора
упругого звена манипулятора
![]() (73)
(73)
и уравнения первого приближения движения упругого звена манипулятора относительно состояний подвижного равновесия нулевого приближения
(74)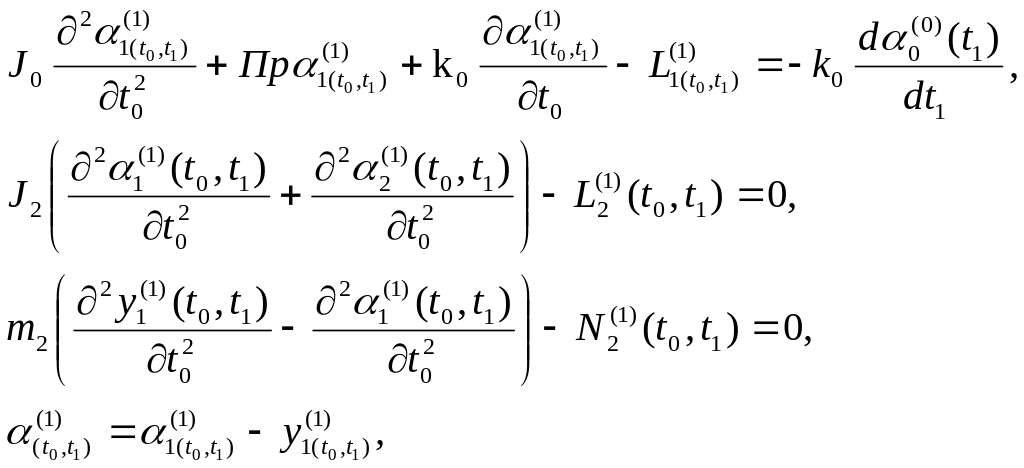
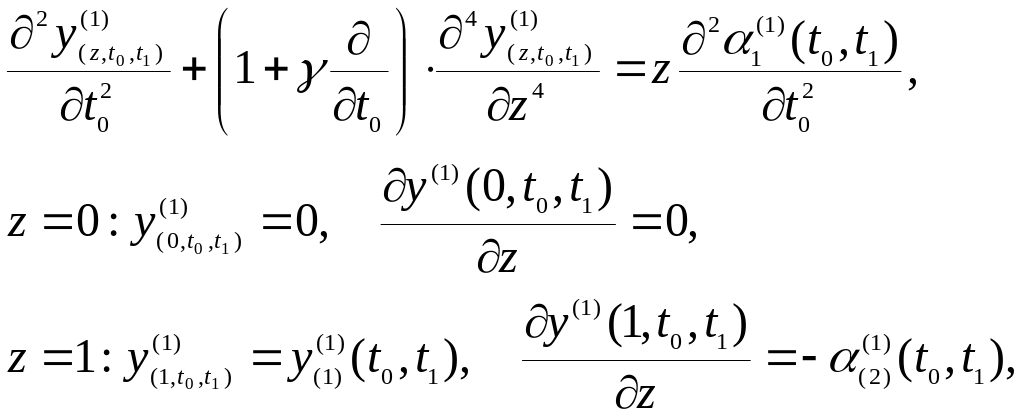
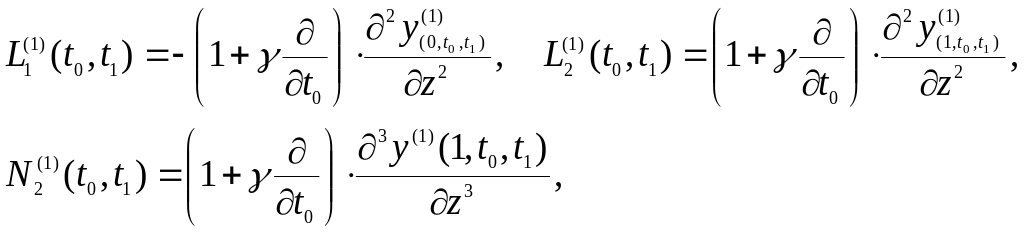

Производя
в системе уравнений (74) прямое интегральное
преобразование Лапласа по быстрому
времени
![]()
![]()
получаем
систему уравнений упругого звена
манипулятора первого приближения в
изображениях. Повторяя рассуждения,
приведенное в учебном пособии
[1, стр.40-44], находим изображение
![]() полярного угла отклонения выходной
точки
полярного угла отклонения выходной
точки
![]() упругого манипулятора от программного
движения нулевого приближения (73) в
форме
упругого манипулятора от программного
движения нулевого приближения (73) в
форме
![]() (75)
(75)


![]()
![]()
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]()
![]() .
.
Задаем теперь программный поворот упругого звена манипулятора в форме линии подвижного равновесия
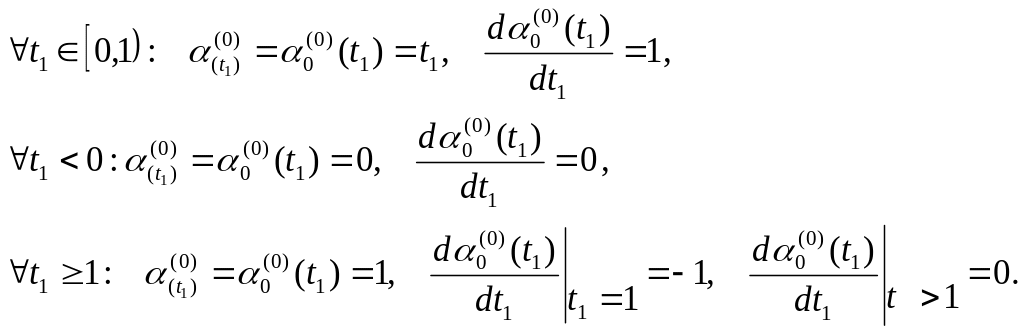 (76)
(76)
Введем принятые в (76) значения
![]()
в формулы (75)
![]() .
(77)
.
(77)
Как
видно здесь
![]() есть изображение переходной функции
системы с передаточной функцией
есть изображение переходной функции
системы с передаточной функцией
![]() ,
а
,
а
![]() есть изображение импульсной переходной
функции системы с передаточной функцией
.
Следовательно, динамическая ошибка
упругого звена манипулятора в режиме
программного поворота (76) на промежутке
есть изображение импульсной переходной
функции системы с передаточной функцией
.
Следовательно, динамическая ошибка
упругого звена манипулятора в режиме
программного поворота (76) на промежутке
![]() вычисляется по формуле
вычисляется по формуле
![]() (78)
(78)
Так
как
![]() есть время окончания программного
поворота упругого звена манипулятора,
которому соответствует значение быстрого
времени
,
то обозначая
и учитывая согласно (76)
есть время окончания программного
поворота упругого звена манипулятора,
которому соответствует значение быстрого
времени
,
то обозначая
и учитывая согласно (76)
![]()
получаем динамическую ошибку системы стабилизации упругого звена манипулятора после окончания программного поворота
![]() .
(79)
.
(79)
Далее полагаем линию подвижного равновесия программного поворота упругого звена манипулятора в форме
![]() (80)
(80)
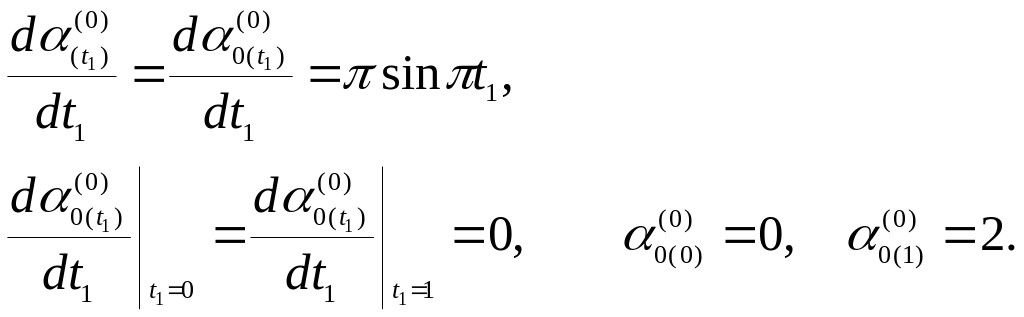
Вводя
(80) в (75), получаем изображение ошибки
стабилизации выходной точки
![]() упругого звена манипулятора относительно
линии (80) подвижного равновесия
упругого звена манипулятора относительно
линии (80) подвижного равновесия
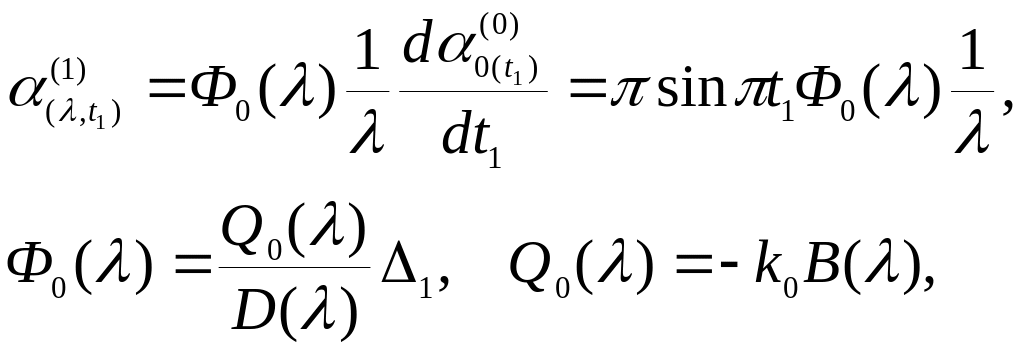 (81)
(81)
![]()
Следовательно
![]() (82)
(82)
