5. Динамическое моделирование системы угловой стабилизации спутника с упругим стержнем и закрепленным на его конце телом по типовым логарифмическим частным характеристикам

Полагая в уравнениях (42) 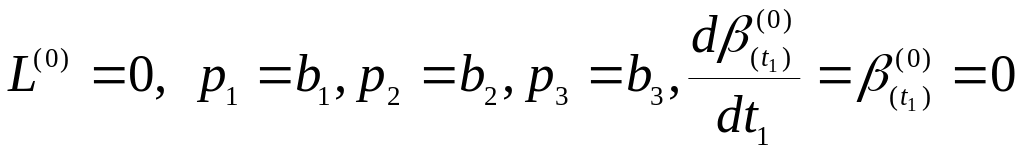и произведя интегральное преобразование Лапласа при нулевых начальных условиях, записываем уравнение возмущенного моментом внешних сил движения спутника в изображениях

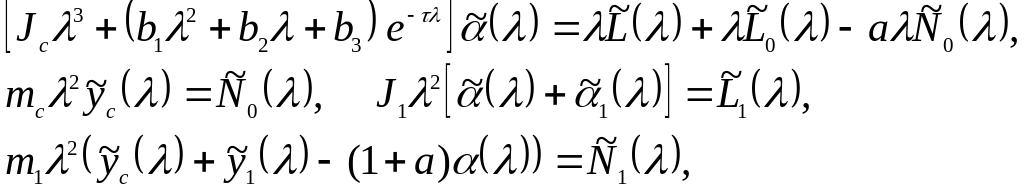
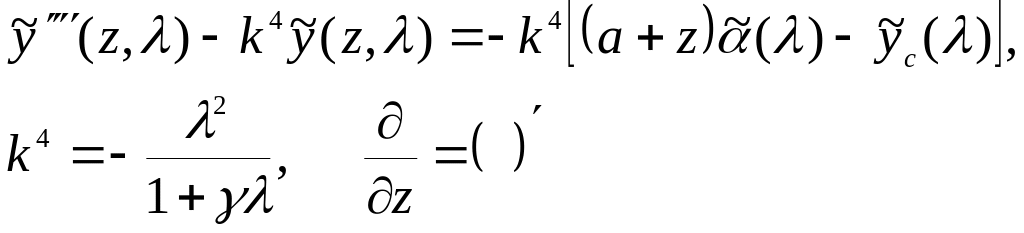(56)

Из системы (56) аналогично предыдущему получаем изображение ошибки стабилизации

(57)

Значения произведены ранее в соотношениях (53).

Построим структурную схему рассматриваемой системы стабилизации применительно к задаче синтеза данной линейной стационарной системы по типовым логарифмическим частотным характеристикам [9], [10]. Полагая коэффициенты обратных связей равными нулю, т.е. , из приведенной в (57) формулы передаточной функции системы стабилизации получаем

(58)

Тогда структурная схема системы стабилизации спутника относительно орбитальной системы координат представляется в виде

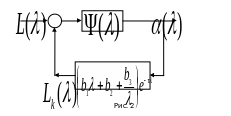
При этом из данной структурной схемы следует передаточная функция разомкнутой системы

(59)

и передаточная функция замкнутой системы стабилизации

(60)

При заданном значении времени запаздывания в газореактивных исполнительных двигателях согласно передаточной функции (59) строится логарифмическая амплитудная частотная характеристика системы в разомкнутом состоянии при некоторых исходных значениях параметров . Затем эти параметры изменяются так, чтобы логарифмическая амплитудная частотная характеристика разомкнутой системы максимально приблизилась к типовой желаемой характеристике. Далее полученные таким образом при заданном времени запаздывания желаемые значения коэффициентов обратных связей вводятся в передаточную функцию замкнутой системы из (57) и вычисляется переходная функция ошибки системы стабилизации при возмущении в форме функции Хевисайда

(61)

Дифференцируя по , получаем импульсную переходную функцию , то есть реакцию системы на возмущение в форме - функции Дирака

(62)

Если в качестве возмущения положить смещенную - функцию , где - произвольное смещение, то из (62) следует весовая функция системы

(63)

Пусть и систему возмущает кусочно – непрерывная и ограниченная функция . Тогда ошибка системы стабилизации вычисляется [2] по формуле

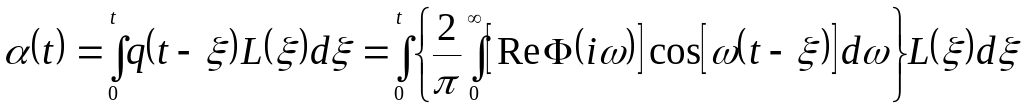(64)

6. Динамическое моделирование программного поворота спутника с упругим стержнем и закрепленным на его конце телом относительно орбитальной системы координат.

Подставляя (39) в первое равенство системы (10), имеем

(65)

где - заданная функция медленного поворота спутника относительно орбитальной системы координат, - динамическая ошибка первого порядка малости системы стабилизации спутника на линии подвижного равновесия . Заметим, что является решением уравнений первого приближения (42). Так как на практике значение постоянного возмущающего момента должно быть существенно меньше наибольшего значения момента сил газореактивных двигателей в режиме насыщения , то полагаем . При этом

(66)

Вводя (66) в уравнения первого приближения (42) и решая эту систему уравнений в изображениях относительно , получаем изображение ошибки стабилизации относительно линии подвижного равновесия

(67)

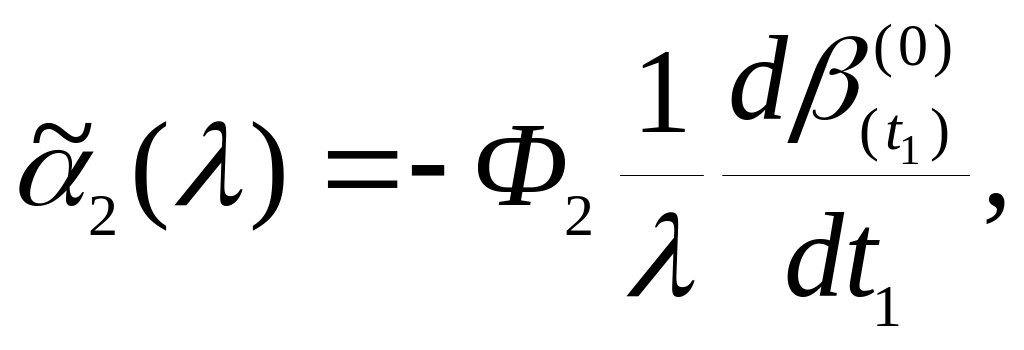
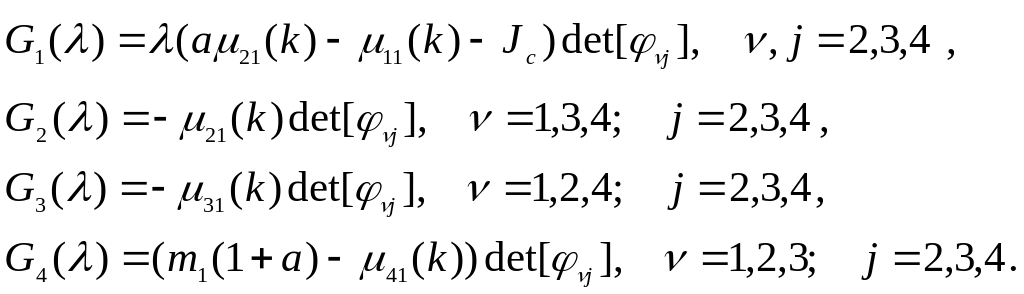
Значения даны в соотношениях (53) с учетом формул из (49).

В свою очередь ошибка стабилизации относительно линии подвижного равновесия выражается через интеграл Меллина

(68)

,

вычисление которого можно провести при помощи эффективного алгоритма [11].

Полагаем далее линию подвижного равновесия в форме

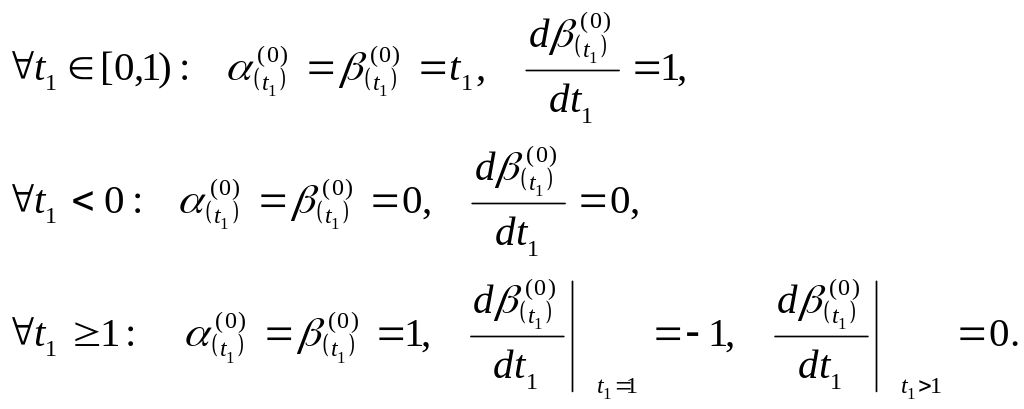(69)

Пусть то есть Тогда вводя и принятые в (69) значения в формулы (67), получаем

(70)

Легко видеть, что есть изображение переходной функции системы с передаточной функцией , есть изображение импульсной переходной функции системы с передаточной функцией .

Следовательно,

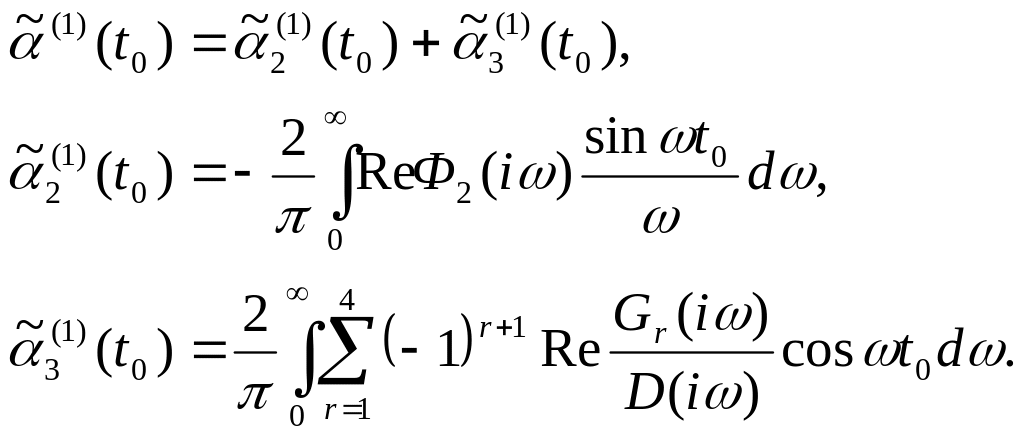(71)

Так как есть время окончания программного поворота спутника, которому соответствует значение быстрого времени , то обозначая и учитывая согласно (69)

получаем динамическую ошибку системы стабилизации спутника после окончания программного поворота

(72)

Далее положим линию подвижного равновесия программного поворота спутника в форме

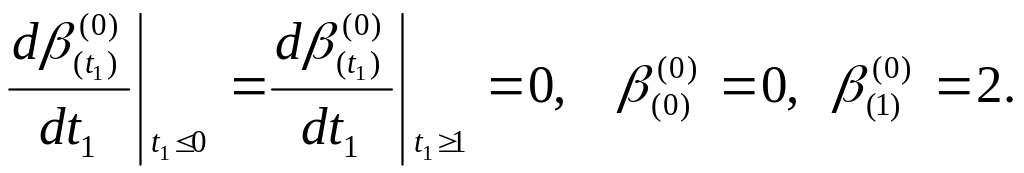
Пусть Тогда при данном программном повороте из (67) следует изображение ошибки стабилизации относительно линии подвижного равновесия

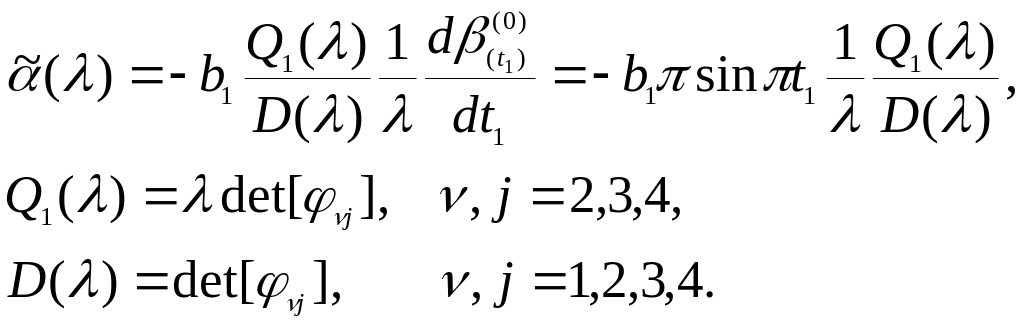
Следовательно

.

Как видно, при данном программном повороте в силу условия , отсутствует динамическая ошибка системы стабилизации спутника при после окончания программного поворота.