3. Решение уравнений нулевого приближения программного поворота спутника относительно орбитальной системы координат при наличии постоянного возмущающего момента внешних сил

Интегрируя однородное дифференциальное уравнение (19) последовательно четыре раза, получаем общее решение

, (28)

- постоянные интегрирования.

Удовлетворяя граничным условиям (20), получаем

.

Решение данной системы алгебраических уравнений имеет вид

. (29)

Покажем далее, что

. (30)

Согласно (28) запишем

. (31)

Так как в соответствии с (18) , то из (21) с учетом (31) следует

. (32)

Вводя (29) в (32), получаем однородную систему алгебраических уравнений

,

Так как определитель данной однородной системы 4-3=1≠0 не равен нулю, то существует только её тривиальное решение

. (33)

Вводя теперь в соответствии с (29) и (32) значение в (28), получаем

. (34)

При этом

. (35)

Итак, равенства (33), (34), (35) подтверждают справедливость утверждения (30). При этом уравнения нулевого приближения (18) – (22) преобразуются в одно уравнение

, (36)

решение которого записывается в форме

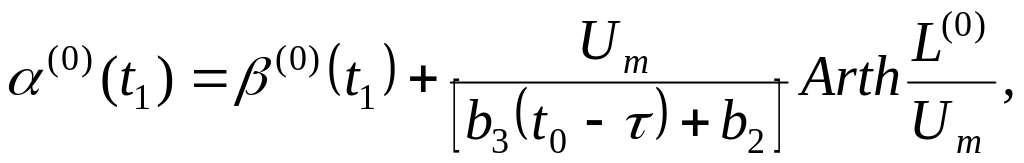
. (37)

Полагаем далее

. (38)

Тогда согласно [7] оптимальные значения коэффициентов интегральной и позиционной обратных связей при изменили свои порядки от до . Следовательно, при быстром возрастании быстрого времени согласно (37), (38) в нулевом приближении установится равенство

. (39)

Замечание. Если положить , то согласно (35) система управления будет иметь статическую ошибку

. (40)

4. Решение уравнений первого приближения движения спутника относительно состояний подвижного равновесия нулевого приближения.

Согласно (30), (36) и (39), принимаем

(41)

.

Вводя соотношения (41) в уравнения (23) – (27), получаем уравнения первого приближения движения спутника относительно состояний подвижного равновесия нулевого приближения

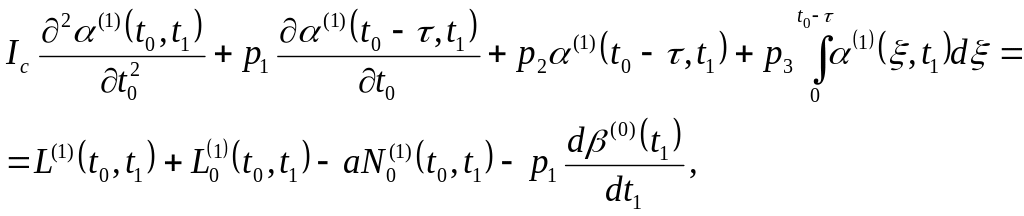
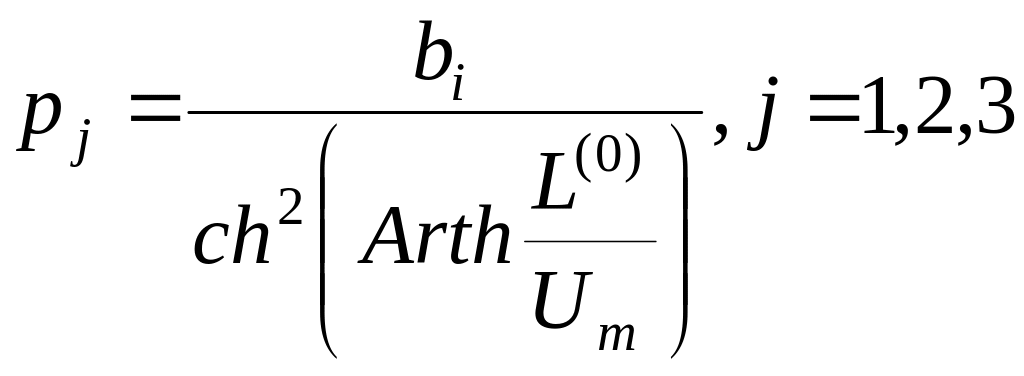(42)

.

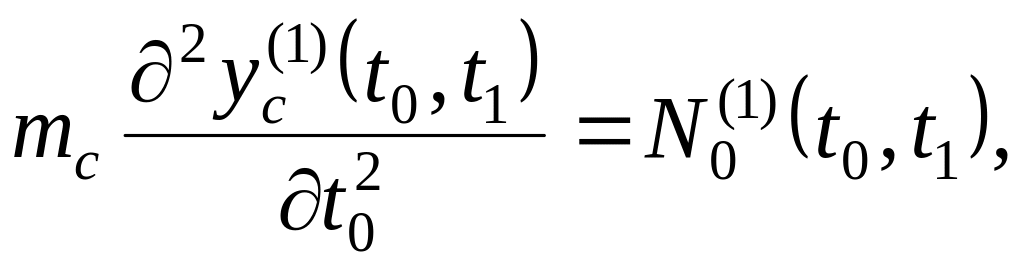
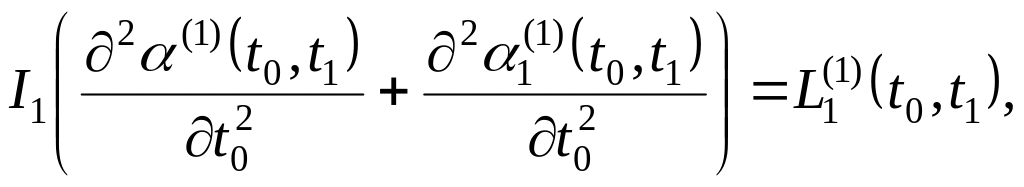
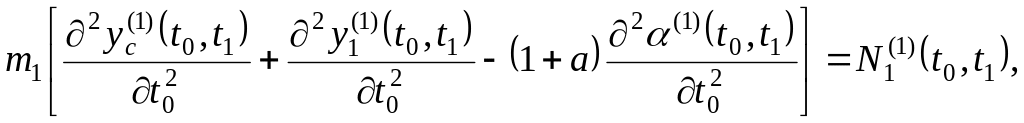
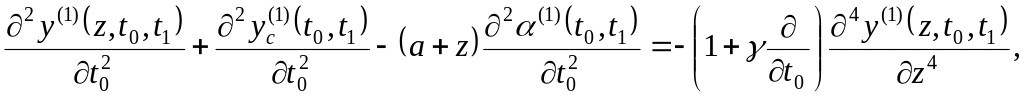
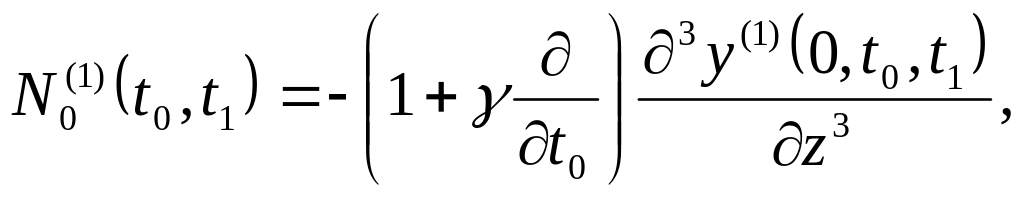
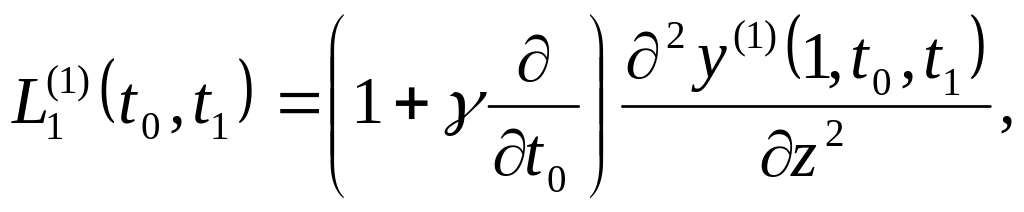
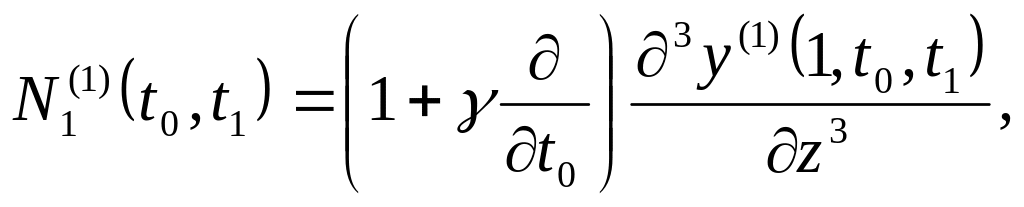
Произведя в уравнениях (42) прямое интегральное преобразование Лапласа по быстрому времени , записываем уравнения первого приближения в изображениях (которые обозначаем тильдой, - произвольный комплексный параметр).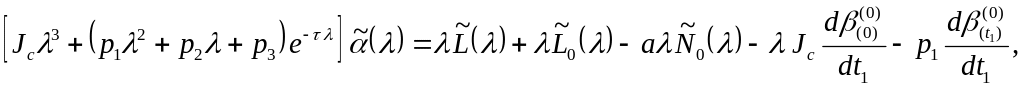 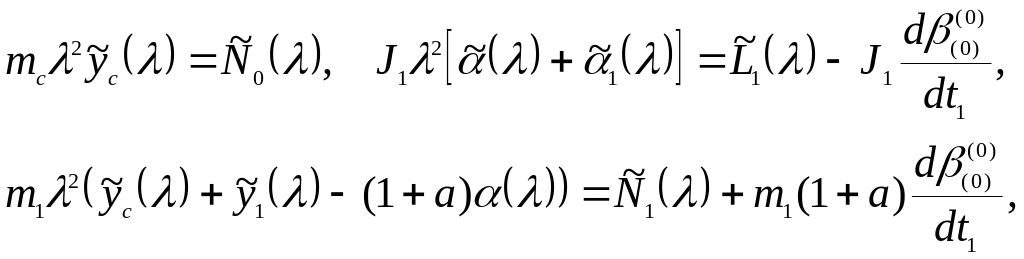(43)

(44)

(45)

(46)

Общее решение линейного неоднородного обыкновенного дифференциального уравнения (44) представляется в форме

(47)

где: , ξ = kz - функции А.Н.Крылова, а константы интегрирования легко находится подстановкой (47) в граничные условия (45).

Далее, вводя (47) в равенства (46), получаем изображения реакций стержня и , действующих (рис.1) соответственно на спутник в точке О и на тело 1 в точке

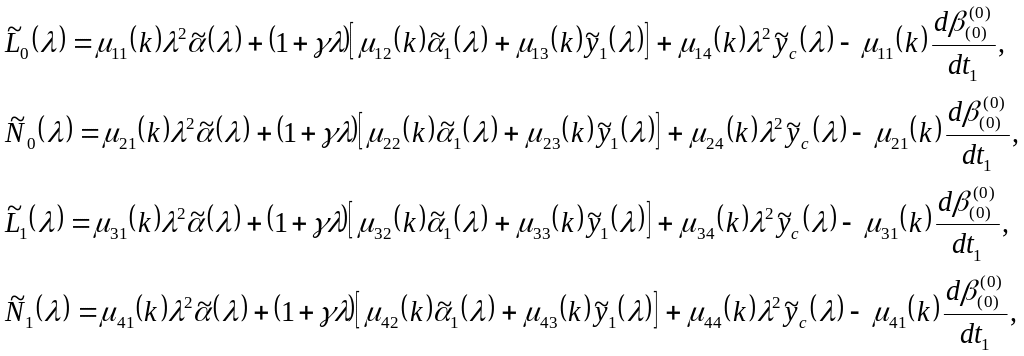(48)

Здесь

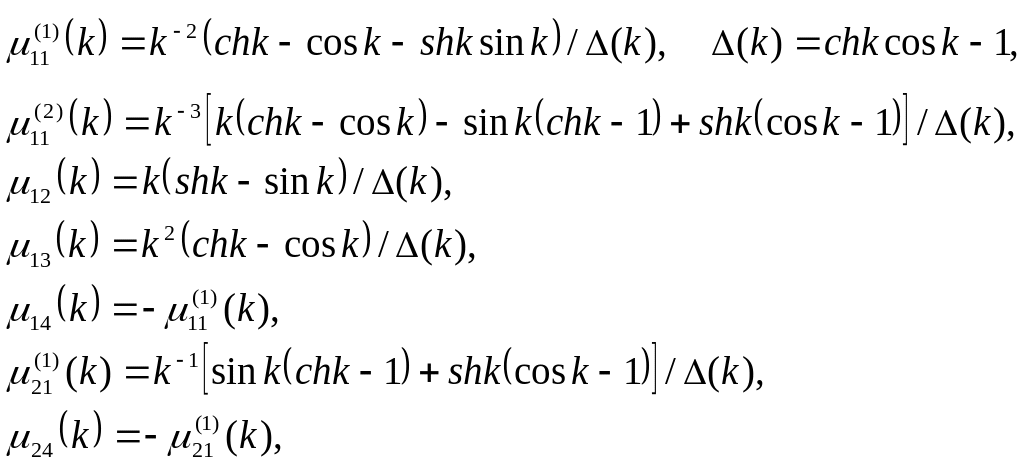
(49)

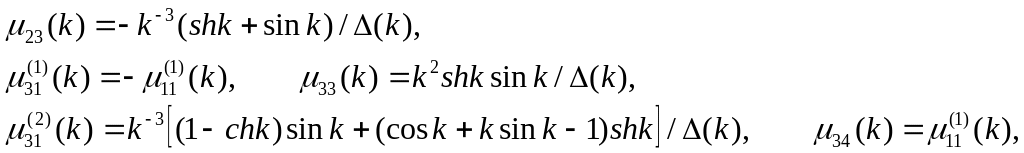
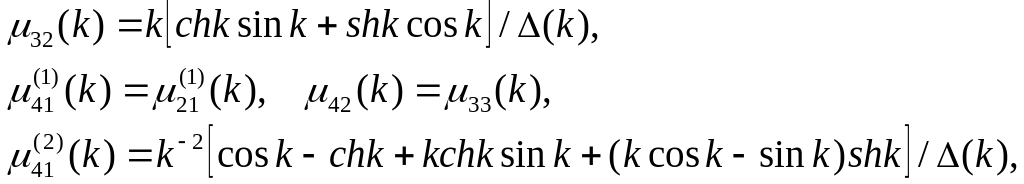
Функции аналитичны в окрестности точки k = 0, а их разложения в ряд Тейлора содержат лишь четные степени параметра k. Знаменатель обнуляется лишь на действительной либо мнимой оси комплексной плоскости. В частности, выбор главной ветви радикалов в выражении для приводит к тому, что при конечных функции , не имеют особенностей в правой половине и на мнимой оси комплексной плоскости . Легко проверить, что функции , обладают следующими свойствами:

(50)

а так же

(51)

Подставляя (48) в (43), сводим задачу к решению неоднородной линейной системы алгебраических уравнений

(52)

k=1 – 4

где

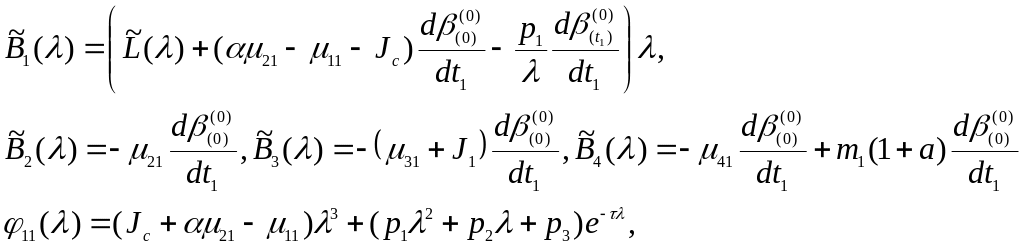
(53)

Решая систему уравнений (52) относительно , получаем изображение ошибки стабилизации

(54)

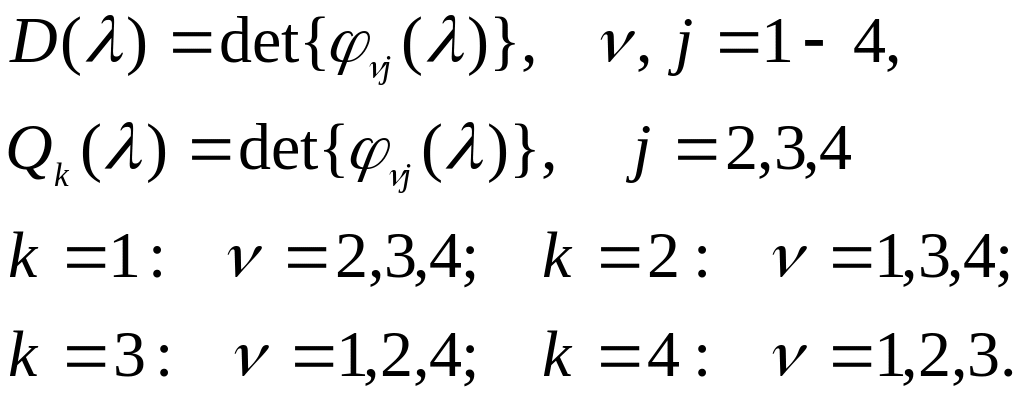(55)

Здесь квазирациональные дроби являются предаточными функциями системы стабилизации;

характеристический квазимногочлен, возмущающие квазимногочлены, трансцендентные функции от , которые выражаются через .