Математическое моделирование управляемых динамических систем
Известно [1], [2], [3] введение в теорию комбинированных динамических систем (КДС). В учебном пособии [1, стр. 95-113] дано математическое обоснование моделирования нелинейных КДС общего вида по методу многих масштабов [4].
Рассматриваются управляемые КДС с ПИД-управлением и нелинейными исполнителнительными органами с ограниченными ресурсами и запаздывающими аргументами применительно к активным системам ориентации и стабилизации космических аппаратов с вязкоупругими элементами и газореактивными двигателями [5-8].
Дано развитие метода синтеза линейных стационарных КДС по типовым логарифмическим частотным характеристикам [9, стр. 231], [10].
1.Уравнения газореактивной системы управления движением спутника с упругим стержнем и закрепленным на его конце телом.
Рассмотрим
плоское движение (Рис. 1) относительно
орбитальной системы координат абсолютно
жесткого спутника с моментом инерции
и массой
под действием возмущающего момента
,
с жестко закрепленным на расстоянии
от центра массы спутника прямолинейным
однородным упругим стержнем, несущим
жестко закрепленное на противоположном
конце, абсолютно жесткое тело с массой
и моментом инерции
.
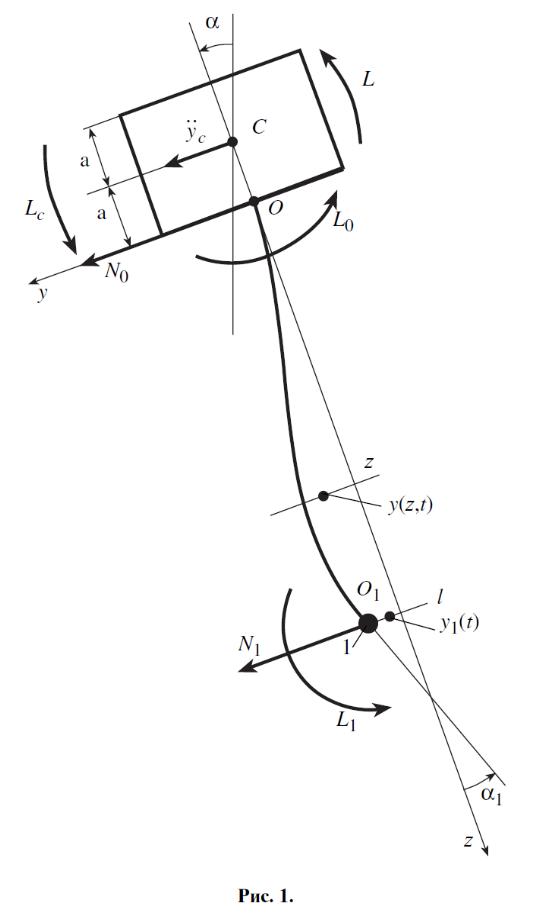
Рис. 1
Полагая
прогибы стержня
значительно меньше его длины
и, следуя методу Ньютона-Эйлера, запишем
уравнения движения данной системы
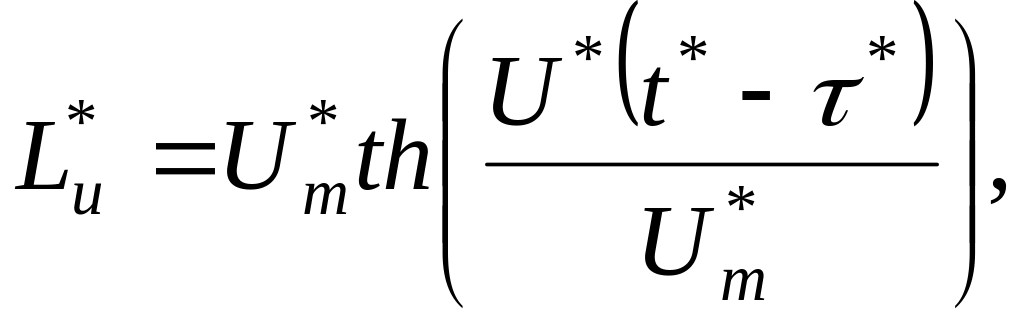
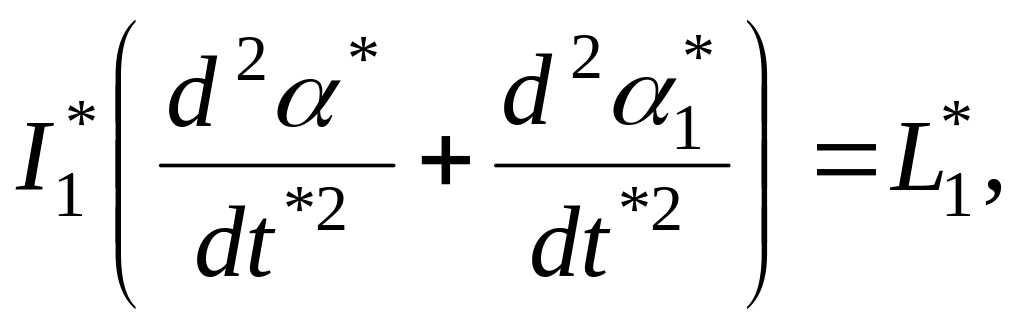(1)
,
,
,
,
.
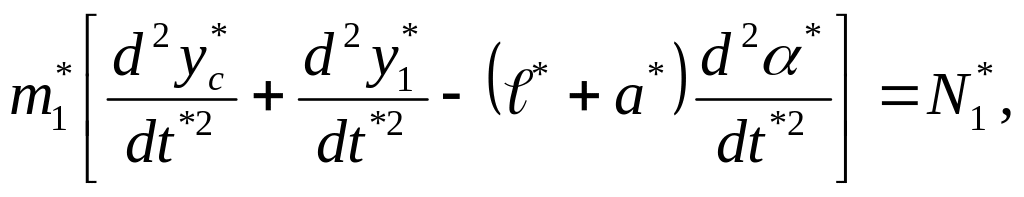
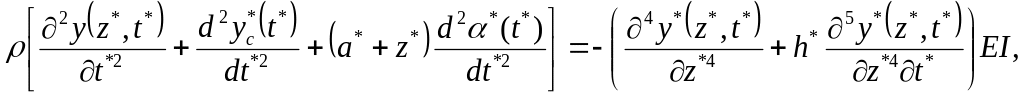
Здесь:
-
возмущающий момент внешних сил;
-
заданная, входная функция угла поворота
спутника
относительно орбитальной системы
координат;
-
управляющий момент сил газореактивных
исполнительных двигателей с нелинейным
типом насыщения и запаздывающим
аргументом
,
-
постоянная времени запаздывания;
-
управление с ПИД - регулятором;
-
коэффициенты соответственно
дифференциальной, позиционной и
интегральной обратных связей;
- наибольший момент сил газореактивных
двигателей в режиме насыщения;
- коэффициент внутреннего трения в
стержне по Фойгту.
Обозначим характерное время в секундах собственного колебания стержня
.
(2)
Где:
– погонная плотность стержня,
(м)
– длина стержня,
-
модуль Юнга,
-
момент инерции поперечного сечения
стержня.
Принимая
характерное значение прогибов стержня
значительно меньше его длины
(м),
введем в рассмотрение безразмерные
переменные и параметры
(3)
,
Выражая размерные переменные и параметры в уравнениях (1) через безразмерные переменные и параметры согласно равенствам (3), запишем безразмерные уравнения газореактивной системы управления движением спутника с упругим стержнем и закрепленным на его конце телом.
Например, согласно (3) имеем:
,
Подставляя эти соотношения в первые три равенства системы (1), получаем:
.
Поделив
эти равенства на
и учитывая
,
записываем
.
Таким образом, исходная система уравнений движения (1) с учетом условий нормировки (3) преобразуется (проверьте самостоятельно) в систему уравнений движения в безразмерных переменных и параметрах
(4)
,
,
,
.
(5)
(6)
,
(7)
,
(8)
образующих
комбинированную динамическую систему
(КДС), где
есть символ производной по времени.
Данная КДС содержит обыкновенные
дифференциальные уравнения (4), динамически
связанные с уравнением с частичными
производными (5) через границы раздела
(6) с условиями связи (7) при нулевых
начальных условиях (8).
Приведенные выше преобразования размерных уравнений движения (1) в безразмерные уравнения (4) - (8) являются обязательными при использовании методов теории возмущений [4].