Определение уравнения регрессии

Найдем среднее значение результатов трех параллельных опытов по каждой строке матрицы планирования следующим образом:

(1)

Средние значения результатов приведены в табл. 4. Общий вид функции при учете взаимодействия факторов имеет следующий вид:

(2)

Определим значения коэффициентов этого полинома:

;

;

;

;

;

;

;

;

Таблица 4. Результаты определения среднего значения параметра и дисперсий воспроизводимости опыта

№ опыта	x0	x1	x2	x3	x1x2	x1x3	x2x3	x1x2x3	уIj, м/ч	уIIj, м/ч	уIIIj, м/ч	yj, м/ч	10-32j	yj, м/ч	yj, %
1	+1	–1	–1	–1	+1	+1	+1	–1	0,36	0,44	0,42	0,41	1,73	0,4068	2,230
2	+1	+1	–1	–1	–1	–1	+1	+1	0,73	0,76	0,74	0,74	0,23	0,7434	0,682
3	+1	–1	+1	–1	–1	+1	–1	+1	0,54	0,59	0,56	0,56	0,63	0,5634	1,645
4	+1	+1	+1	–1	+1	–1	–1	–1	0,86	0,88	0,87	0,87	0,10	0,8700	0,575
5	+1	–1	–1	+1	+1	–1	–1	+1	0,42	0,49	0,45	0,45	1,23	0,4532	2,000
6	+1	+1	–1	+1	–1	+1	–1	–1	0,88	0,89	0,88	0,88	0,03	0,8834	0,558
7	+1	–1	+1	+1	–1	–1	+1	–1	0,63	0,66	0,65	0,65	0,23	0,6466	1,433
8	+1	+1	+1	+1	+1	+1	+1	+1	0,99	1	0,98	0,99	0,10	0,9900	0,505

С учетом вычисленных коэффициентов математическая модель примет вид:

Проверка воспроизводимости результатов экспериментов

Для каждой строки плана рассчитаем дисперсию воспроизводимости опыта следующим образом:

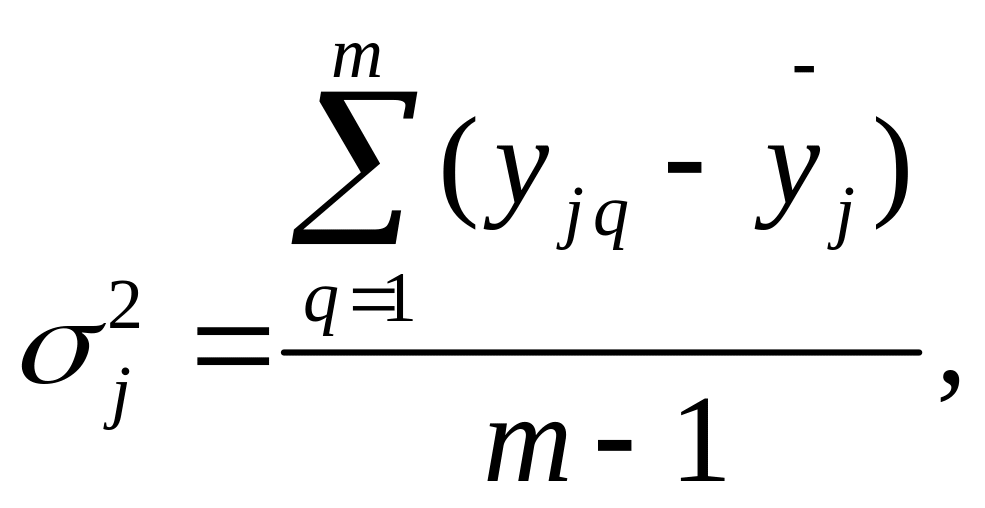(3)

Значения дисперсий приведены в табл. 4. Затем просуммируем дисперсии:

.

Выберем среди дисперсий наибольшую и определим G-критерий Кохрена:

(4)

Табличное значение G-критерия Кохрена равно

G_{=0,05, f1=2, f2=8}=0,5157.

Так как G<G_,f1,f2, то можно сделать вывод о том, что с доверительной вероятностью 0,95 дисперсии опытов однородны, и гипотеза о воспроизводимости результатов экспериментов принимается.

Определяем дисперсию воспроизводимости всего эксперимента:

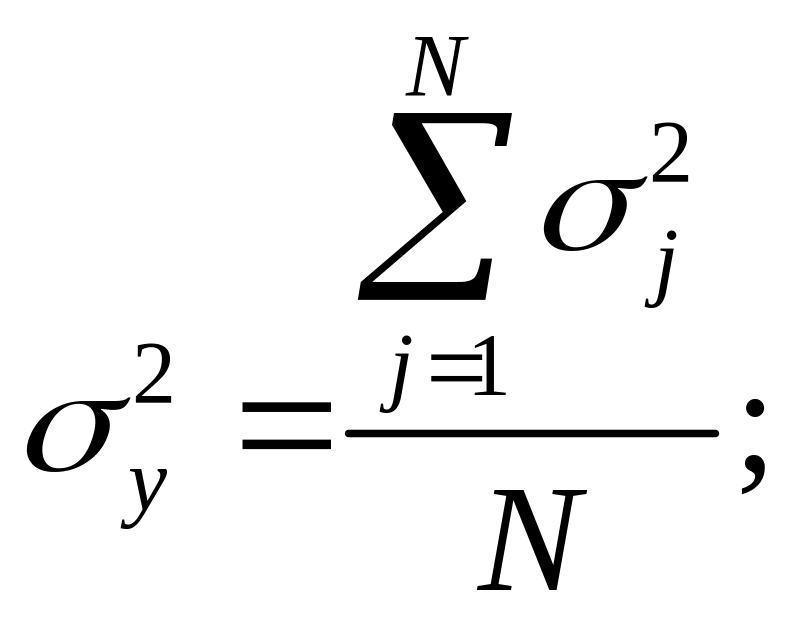. (5)

.