Билет 14
Методика вычисления вероятности по формулам полной вероятности и Бейеса
Пусть
событие A может
наступить только с одним из n попарно
несовместных событий
,
которые по отношению к А называются гипотезами.
Тогда вероятность
события А можно
вычислить по формуле полной
вероятности:
.
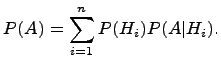
Если стало известно, что событие А произошло,
то вероятность 
можно
переоценить, т.е. найти условные
вероятности 
.
Эта задача решается по
формуле Байеса:
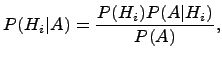
где 
вычисляется по
формуле полной вероятности.
Пример.
В первой урне 2 белых и 6 черных шаров, во второй – 4 белых и 2 черных. Из первой урны наудачу переложили 2 шара во вторую, после чего из второй урны наудачу достали один шар.
а) Какова вероятность того, что этот шар белый?
б) Шар, взятый из второй урны, оказался белым. Какова вероятность того, что из первой урны во вторую были переложены 2 белых шара?
Решение.
Введем обозначения:
А – шар, извлеченный из второй урны, белый;
гипотезы 
–
из первой урны во вторую переложены 2
белых шара,
–
переложены
2 разноцветных шара,
–
переложены
2 черных шара.
Тогда
Вероятности
гипотез 
и
условие вероятности 
вычисляем
по классической схеме:
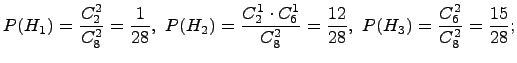
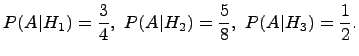
Полученные результаты подставим в формулу полной вероятности:
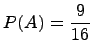
б)
Вероятность 
находим
по формуле
Байеса:
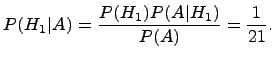
Генеральная и выборочная статистические совокупности Статистическая совокупность
Статистическая совокупность состоит из материально существующих объектов (Работники, предприятия, страны, регионы), является объектом статистического исследования.Статистическая совокупность - множество единиц, обладающих массовостью, типичностью, качественной однородностью и наличием вариации.
Единица совокупности — каждая конкретная единица статистической совокупности.
Одна и таже статистическая совокупность может быть однородна по одному признаку и неоднородна по другому.
Качественная однородность — сходство всех единиц совокупности по какому-либо признаку и несходство по всем остальным.
В статистической совокупности отличия одной единицы совокупности от другой чаще имеют количественную природу. Количественные изменения значений признака разных единиц совокупности называются вариацией.
Вариация признака — количественное изменение признака (для количественного признака) при переходе от одной единицы совокупности к другой.
Признак - это свойство, характерная черта или иная особенность единиц, объектов и явлений, которая может быть наблюдаема или измерена. Признаки делятся на количественные и качественные. Многообразие и изменчивость величины признака у отдельных единиц совокупности называется вариацией.
Атрибутивные (качественные) признаки не поддаются числовому выражению (состав населения по полу). Количественные признаки имеют числовое выражение (состав населения по возрасту).
Показатель — это обобщающая количественно качестванная характеристика какого-либо свойства единиц или совокупности в цельм в конкретных условиях времени и места.
Система показателей — это совокупность показателей всесторонне отражающих изучаемое явление.
Например, изучается зарплата:
Признак — оплата труда
Статистическая совокупность — все работники
Единица совокупности — каждый работник
Качественная однородность — начисленная зарплата
Вариация признака — ряд цифр