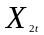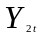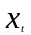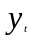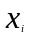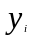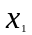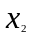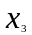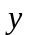1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
2. Примените тест Голдфелда-Квандта для изучения гипотезы об отсутствии гетероскедастичности остатков.
3.
В случае гетероскедастичности остатков
примените взвешенный метод наименьших
квадратов, предполагая, что дисперсии
отклонений
пропорциональны
.
4. Определите, существенно ли повлияла гетероскедастичность на качество оценок в уравнении, построенном по обычному методу наименьших квадратов.
Задача 3
Рассчитайте
стандартные ошибки
коэффициентов модели линейной регрессии,
если
,
.
Задача 4
Имеются следующие данные об остатках парной линейной регрессии
(
-
номер момента наблюдения)
.
Сделайте вывод о наличии или отсутствии автокорреляции, применив тест Дарбина- Уотсона.
Задача 5
Имеется следующая модель денежного и товарного рынков:
где
– процентная ставка;
–
ВВП;
–
денежная масса;
–
инвестиции;
–
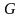государственные расходы,
– текущий период.
Исследуйте идентифицируемость каждого уравнения системы. Запишите приведенную форму модели.
Вариант 4.
Задача 1.
Имеется информация по 10 предприятиям о зависимости себестоимости (ден. ед.) единицы продукции от трудоемкости единицы продукции (чел -час):
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
10,3 |
11,2 |
12,3 |
11,8 |
14,6 |
15,8 |
15,2 |
14,2 |
13,1 |
10,8 |
Y |
110 |
125 |
130 |
131 |
150 |
172 |
158 |
145 |
140 |
118 |
1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
2. Проверьте статистическую значимость оценок теоретических коэффициентов при уровне значимости .
3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
4.
Спрогнозируйте себестоимость при
трудоемкости
и рассчитайте 95% доверительный интервал
для условного математического ожидания
.
5. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных значений себестоимости при трудоемкости .
6. Оцените на сколько изменится себестоимость, если трудоемкость вырастет на 1 чел-час.
7. Рассчитайте коэффициент детерминации .
8. Рассчитайте - статистику для коэффициента детерминации и оцените его статистическую значимость.
Задача 2.
Предполагается,
что объем предложения некоторого блага
для
функционирующей в условиях конкуренции
фирмы зависит линейно от цены
данного блага и от заработной платы
сотрудников фирмы, производящих данное
благо:
.
X1 |
10 |
15 |
20 |
25 |
40 |
37 |
43 |
35 |
38 |
55 |
50 |
35 |
40 |
45 |
X2 |
12 |
10 |
9 |
9 |
8 |
8 |
6 |
4 |
4 |
5 |
3 |
1 |
2 |
1 |
Y |
20 |
35 |
30 |
45 |
60 |
69 |
75 |
90 |
105 |
110 |
120 |
130 |
130 |
135 |
1. Оцените по методу наименьших квадратов коэффициенты уравнения регрессии.
2. Проверьте качество построенной модели на основе -статистики и - статистики.
Задача 3
При
расчете коэффициентов уравнения
регрессии
была допущена ошибка при определении
коэффициента
(коэффициент
вычислен правильно). В результате
получили
.
Сумма остатков оказалась равной
.
Определите коэффициент
.
Задача 4
Коэффициент
корреляции между переменными
и
равен 0,9. Каким будет коэффициент
детерминации в случае линейной модели
регрессии?
Задача 5
Имеется следующая система одновременных уравнений:
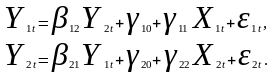
Оцените параметры данной модели косвенным методом наименьших квадратов, если имеются следующие данные
|
|
|
|
|
1 |
1 |
3 |
3,2 |
4,0 |
2 |
2 |
8 |
10,0 |
10,2 |
3 |
2 |
1 |
2,8 |
5,9 |
4 |
3 |
9 |
12,2 |
15,8 |
5 |
4 |
9 |
14,2 |
18,9 |
6 |
5 |
1 |
6,2 |
13,4 |
7 |
7 |
8 |
15,3 |
27,4 |
8 |
5 |
5 |
8,3 |
15,7 |
9 |
9 |
1 |
11,5 |
22,9 |
10 |
7 |
9 |
15,3 |
26,9 |
Вариант 5.
Задача 1.
Имеется информация по 10 предприятиям о зависимости удельных постоянных расходов от объема выпускаемой продукции :
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
1000 |
900 |
950 |
1020 |
1100 |
950 |
1150 |
1200 |
1220 |
1250 |
Y |
800 |
720 |
730 |
800 |
845 |
745 |
890 |
940 |
922 |
960 |
1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
2. Проверьте статистическую значимость оценок теоретических коэффициентов при уровне значимости .
3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
4.
Спрогнозируйте постоянные расходы при
объеме выпуска
и рассчитайте 95% доверительный интервал
для условного математического ожидания
.
5. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных постоянных расходов при объеме выпуска .
6. Оцените на сколько единиц изменится значение постоянных расходов, если объем выпуска вырастет на 100.
7. Рассчитайте коэффициент детерминации .
8. Рассчитайте - статистику для коэффициента детерминации и оцените его статистическую значимость.
Задача 2.
Выберите подходящую нелинейную модель, линеаризуйте ее и оцените параметры, если имеются следующие данные ( - объясняющая переменная, - зависимая переменная).
X |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Y |
5 |
12,3 |
20,9 |
30,3 |
40,5 |
51,4 |
62,7 |
74,6 |
87,0 |
99,8 |
Задача 3
Рассматривается
модель
.
Получены матрицы
.
Рассчитайте
оценки
параметров
модели.
Задача 4
Чему
равны коэффициент детерминации
-
статистика в случае строгой функциональной
зависимости
от
?
Задача 5
Какой из нижеприведенных процессов является стационарным?
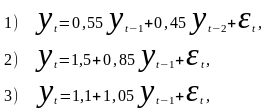
где
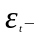«белый шум» с нулевым математическим
ожиданием.
Вариант 6.
Задача 1.
Имеется информация по 10 предприятиям о потреблении материалов от объема производства продукции :
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
105 |
116 |
123 |
137 |
145 |
161 |
173 |
187 |
201 |
218 |
Y |
210 |
240 |
270 |
290 |
300 |
320 |
350 |
400 |
400 |
450 |
1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
2. Проверьте статистическую значимость оценок теоретических коэффициентов при уровне значимости .
3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
4.
Спрогнозируйте потребление материалов
при объеме производства
и рассчитайте 95% доверительный интервал
для условного математического ожидания
.
5. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных объемов потребления материалов при объеме производства .
6. Оцените на сколько изменится потребление материалов, если доход вырастет на 10.
7. Рассчитайте коэффициент детерминации .
8. Рассчитайте - статистику для коэффициента детерминации и оцените его статистическую значимость.
Задача 2
Выберите подходящую нелинейную модель, линеаризуйте ее и оцените параметры, если имеются следующие данные ( - объясняющая переменная, - зависимая переменная):
X |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
Y |
5,5 |
5,7 |
6,3 |
6,6 |
7,1 |
7,7 |
8,12 |
9,1 |
9,3 |
10 |
Задача 3
Коэффициент корреляции двух переменных и равен 0,85. Чему будет равен коэффициент корреляции, если все значения переменных и умножить на -10?
Задача 4
Как ведет себя зависимая переменная с ростом объясняющей переменной в модели линейной регрессии, если коэффициент корреляции меньше, чем коэффициент детерминации?
Задача 5
Для
модели парной линейной регрессии
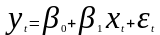имеются данные за 10 лет
|
5,1 |
2,6 |
1,9 |
6,9 |
9,1 |
3,9 |
6,6 |
9,1 |
1,1 |
3,6 |
|
5,1 |
4,9 |
3,2 |
8,3 |
8,7 |
5,6 |
6,6 |
11,2 |
2,2 |
4,6 |
Оценить
параметры модели обобщенным методом
наименьших квадратов, если для случайного
возмущения имеется авторегрессия
первого порядка
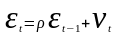с известным значением
.
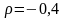Вариант 7.
Задача 1.
Имеется информация по 10 предприятиям концерна об объеме продаж (млн.руб.) от затрат на рекламу (млн.руб.).
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
1,1 |
1,2 |
1,3 |
1,5 |
1,6 |
1,5 |
1,9 |
2,1 |
2,2 |
2,3 |
Y |
23,1 |
23,6 |
24,2 |
23,1 |
25,2 |
25,1 |
26,7 |
26,3 |
27,1 |
26,9 |
1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
2. Проверьте статистическую значимость оценок теоретических коэффициентов при уровне значимости .
3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
4.
Спрогнозируйте объем продаж при затратах
на рекламу
и рассчитайте 95% доверительный интервал
для условного математического ожидания
.
5. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных объемов продаж при затратах на рекламу .
6. Оцените на сколько изменится объем продаж, если расходы на рекламу вырастут на 0,1 млн.руб.
7. Рассчитайте коэффициент детерминации .
8. Рассчитайте - статистику для коэффициента детерминации и оцените его статистическую значимость.
Задача 2.
Даны следующие данные ( - объясняющая переменная, - зависимая переменна). Выберите подходящую нелинейную модель, линеаризуйте ее и оцените параметры.
X |
10,0 |
11,7 |
13,7 |
16,0 |
18,7 |
21,9 |
25,7 |
30,0 |
35,1 |
41,1 |
Y |
15,0 |
13,0 |
11,0 |
11,2 |
10,3 |
9,4 |
8,9 |
8,1 |
7,6 |
7,44 |
Задача 3
Построены две эмпирических модели
(1)
,
(2)
.
Коэффициенты детерминации соответственно равны
(1)
,
(2)
.
Можно ли сказать, что уравнение (2) лучше описывает исходные данные, чем уравнение (1)? Ответ обосновать.
Задача 4
Если
построить модель
,
где
- прибыль,
доход,
затраты,
то какими будут коэффициенты регрессии?
Задача 5
Для модели парной линейной регрессии имеются данные за 10 лет
|
5,1 |
2,6 |
1,9 |
6,9 |
9,1 |
3,9 |
6,6 |
9,1 |
1,1 |
3,6 |
|
5,1 |
4,9 |
3,2 |
8,3 |
8,7 |
5,6 |
6,6 |
11,2 |
2,2 |
4,6 |
Оценить для случайного возмущения коэффициент авторегрессии первого порядка.
Вариант 8.
Задача 1.
Имеется информация по 10 предприятиям оптовой торговли об объеме реализации относительно размера торговой площади :
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
700 |
750 |
800 |
830 |
850 |
900 |
920 |
950 |
980 |
890 |
Y |
6350 |
7800 |
7600 |
8600 |
8600 |
9200 |
9000 |
9100 |
9950 |
9000 |
1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
2. Проверьте статистическую значимость оценок теоретических коэффициентов при уровне значимости .
3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
4.
Спрогнозируйте объем реализации при
размере торговой площади
и рассчитайте 95% доверительный интервал
для условного математического ожидания
.
5. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных объемов реализации при торговой площади .
6. Оцените на сколько единиц изменится объем реализации, если площадь вырастет на 100 .
7. Рассчитайте коэффициент детерминации .
8. Рассчитайте - статистику для коэффициента детерминации и оцените его статистическую значимость.
Задача 2.
Имеются данные о динамике оборота розничной торговли и потребительских цен региона за два года. Используя метод Ш.Алмон, оцените параметры модели с распределенным лагом. Длину лага выберите не более 4, степень аппроксимирующего полинома – не более 3. Оцените качество построенной модели.
Месяц |
Оборот розничной торговли, % к предыдущему месяцу |
Индекс потребительских цен, % к предыдущему месяцу |
Январь |
70,8 |
101,7 |
Февраль |
98,7 |
101,1 |
Март |
97,9 |
100,4 |
Апрель |
99,6 |
100,1 |
Май |
96,1 |
100,0 |
Июнь |
103,4 |
100,1 |
Июль |
95,5 |
100,0 |
Август |
102,9 |
105,8 |
Сентябрь |
77,6 |
145,0 |
Октябрь |
102,3 |
99,8 |
Ноябрь |
102,9 |
102,7 |
Декабрь |
123,1 |
109,4 |
Январь |
74,3 |
110,0 |
Февраль |
92,9 |
106,4 |
Март |
106,0 |
103,2 |
Апрель |
99,8 |
103,2 |
Май |
105,2 |
102,9 |
Июнь |
99,7 |
100,8 |
Июль |
99,7 |
101,6 |
Август |
107,9 |
101,5 |
Сентябрь |
98,8 |
101,4 |
Октябрь |
104,6 |
101,7 |
Ноябрь |
106,4 |
101,7 |
Декабрь |
122,7 |
101,2 |
Задача 3
(1) - теоретическое уравнение регрессии,
(2) - эмпирическое уравнение регрессии.
Какое из уравнений и почему лучше описывает выборочные данные?
Задача 4
Если
построить модель
,
где
прибыль,
доход,
затраты,
то каким будет коэффициент детерминации?
Задача 5
Какое условие Гаусса-Маркова не выполняется, если ковариационная матрица случайных возмущений имеет вид
,
где диагональные элементы не равны между собой?
Вариант 9.
Задача 1.
Имеется информация по 10 предприятиям оптовой торговли об объеме реализации относительно товарных запасов :
Годы |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
X |
11,1 |
11,6 |
12,3 |
12,8 |
13,3 |
13,6 |
13,9 |
14,5 |
16,8 |
18,2 |
Y |
70,1 |
73,3 |
77,1 |
76,1 |
80,1 |
76,5 |
79,5 |
81,5 |
86,8 |
91,5 |
1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
2. Проверьте статистическую значимость оценок теоретических коэффициентов при уровне значимости .
3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
4.
Спрогнозируйте объем реализации при
товарных запасах
и рассчитайте 95% доверительный интервал
для условного математического ожидания
.
5. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных объемов реализации при уровне запасов .
6. Оцените на сколько единиц изменится объем реализации, если товарные запасы вырастут на 1.
7. Рассчитайте коэффициент детерминации .
8. Рассчитайте - статистику для коэффициента детерминации и оцените его статистическую значимость.
Задача 2.
На предприятии используются станки двух фирм (А,В). Исследуется надежность этих станков. Учитывается возраст станка ( , в месяцах) и время ( , в часах) безаварийной работы до последней поломки. Выборка из 36 станков дала следующие результаты.
Фирма |
|
|
Фирма |
|
|
А |
23 |
280 |
А |
52 |
200 |
А |
69 |
176 |
А |
66 |
123 |
А |
63 |
176 |
А |
20 |
245 |
А |
52 |
200 |
А |
48 |
236 |
А |
66 |
123 |
В |
30 |
230 |
А |
20 |
245 |
В |
25 |
216 |
А |
48 |
236 |
В |
75 |
45 |
А |
25 |
240 |
В |
20 |
265 |
А |
71 |
115 |
В |
40 |
176 |
А |
40 |
225 |
В |
25 |
260 |
А |
30 |
260 |
В |
69 |
65 |
А |
75 |
100 |
В |
45 |
126 |
А |
56 |
170 |
В |
69 |
45 |
А |
37 |
240 |
В |
22 |
220 |
А |
67 |
120 |
В |
33 |
194 |
А |
23 |
280 |
В |
21 |
240 |
А |
69 |
176 |
В |
50 |
120 |
А |
63 |
176 |
В |
56 |
88 |
Оцените
уравнение регрессии
,
учитывающее различие качества станков
разных фирм.
Задача 3
Выведите
непосредственно методом наименьших
квадратов формулу для оценки коэффициента
наклона в регрессии без свободного
члена, т.е. найдите оценку параметра
в регрессии
минимизацией суммы квадратов отклонений
. .
Задача 4
Как ведет себя зависимая переменная с ростом объясняющей переменной в модели линейной регрессии, если коэффициент корреляции больше, чем коэффициент детерминации?
Задача 5
Для
обобщенной линейной регрессионной
модели
имеются 10 пар наблюдений
|
8 |
12 |
10 |
20 |
16 |
20 |
24 |
28 |
30 |
36 |
|
6,8 |
7,3 |
6,9 |
8,6 |
7,4 |
8,0 |
8,8 |
8,0 |
9,9 |
10,3 |
Определить оценки обобщенного метода наименьших квадратов, если ковариационная матрица случайных возмущений имеет вид
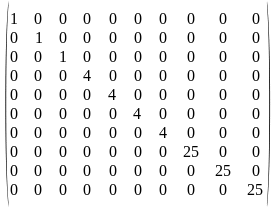
Вариант 10.
Задача 1.
Имеется информация за 10 лет относительно среднего дохода и среднего потребления (млн.руб.):
Годы |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
X |
10,5 |
11,6 |
12,3 |
13,7 |
14,5 |
16,1 |
17,3 |
18,7 |
20,1 |
21,8 |
Y |
8,12 |
10,0 |
8,41 |
12,0 |
12,4 |
11,4 |
12,8 |
13,9 |
17,3 |
17,5 |
1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
2. Проверьте статистическую значимость оценок теоретических коэффициентов при уровне значимости .
3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
4.
Спрогнозируйте потребление при доходе
и рассчитайте 95% доверительный интервал
для условного математического ожидания
.
5.
Рассчитайте границы интервала, в котором
будет сосредоточено не менее 95% возможных
объемов потребления при доходе
.
6. Оцените на сколько изменится потребление, если доход вырастет на 3 млн.руб.
7. Рассчитайте коэффициент детерминации .
8. Рассчитайте - статистику для коэффициента детерминации и оцените его статистическую значимость.
Задача 2
Имеется следующая модель кейнсианского типа:
где
Переменные
являются эндогенными.
Определите, идентифицировано ли каждое из уравнений модели. Напишите приведенную форму модели.
Задача 3.
Для
оценки коэффициентов уравнения регрессии
вычисления проведены в матричной форме.
Определите эмпирические коэффициенты регрессии.
Задача 4.
Коэффициент детерминации между переменными и равен 0,64. Каким будет коэффициент корреляции в случае линейной модели регрессии?
Задача 5
Для
модели
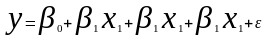имеются следующие данные
|
10 |
5 |
1 |
3 |
10 |
1 |
4 |
9 |
11 |
8 |
|
20 |
11 |
2 |
4 |
22 |
2 |
10 |
18 |
22 |
16 |
|
1 |
10 |
1 |
10 |
5 |
5 |
5 |
7 |
7 |
1 |
|
33 |
34 |
5 |
30 |
45 |
13 |
25 |
40 |
47 |
26 |
Оцените коэффициенты модели, используя «гребневой» метод. Используйте дополнительный параметр равный 0,4.