
- •Варианты контрольной работы
- •1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
- •1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
- •3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
- •7. Рассчитайте коэффициент детерминации .
- •8. Рассчитайте - статистику для коэффициента детерминации и оцените его статистическую значимость.
- •1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
Варианты контрольной работы
Номер варианта контрольной работы можно выбрать, воспользовавшись следующей таблицей.
Первая буква фамилии студента |
Номер варианта |
А,Л,Х |
1 |
Б,М,Ч |
2 |
В,Н,Щ |
3 |
Г,О,Ы |
4 |
Д,П,Э |
5 |
Е,Ё,Р,Ю |
6 |
Ж,С,Я |
7 |
З,Т,Ш |
8 |
И,Й,У |
9 |
К,Ф,Ц |
10 |
Вариант 1
Задача 1
Случайная
величина
 распределена по нормальному закону с
параметрами
распределена по нормальному закону с
параметрами
 .
.
Записать выражения функции плотности и функции распределения случайной величины. При каком значении функция плотности принимает максимальное значение?
Задача 2
Имеется
информация за 10 лет относительно среднего
дохода
![]() и
среднего потребления
и
среднего потребления
![]() (млн.руб.):
(млн.руб.):
Годы |
2000 |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
2008 |
2009 |
X |
10,5 |
11,6 |
12,3 |
13,7 |
14,5 |
16,1 |
17,3 |
18,7 |
20,1 |
21,8 |
Y |
8,12 |
10,0 |
8,41 |
12,1 |
12,4 |
11,4 |
12,8 |
13,9 |
17,3 |
17,5 |
1.
Оцените коэффициенты линейной регрессии
![]() по методу наименьших квадратов.
по методу наименьших квадратов.
2.
Проверьте статистическую значимость
оценок
![]() теоретических коэффициентов
теоретических коэффициентов
![]() при уровнях значимости
при уровнях значимости
![]() .
.
3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
4.
Спрогнозируйте потребление при доходе
![]() и рассчитайте 95% доверительный интервал
для условного математического ожидания
и рассчитайте 95% доверительный интервал
для условного математического ожидания
![]() .
.
5. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных объемов потребления при доходе .
6. Оцените на сколько изменится потребление, если доход вырастет на 3 млн.руб.
7.
Рассчитайте коэффициент детерминации
![]() .
.
8.
Рассчитайте
![]() -
статистику для коэффициента детерминации
и оцените его статистическую значимость.
-
статистику для коэффициента детерминации
и оцените его статистическую значимость.
Задача 3
По 15 наблюдениям получены следующие результаты:
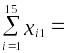 120,
120,
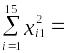 1240,
1240,
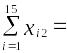 104,
104,
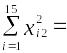 1004,
1004,
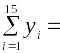 590,
590,
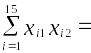 936,
936,
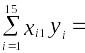 5732,
5732,
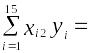 4841,
4841,
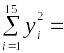 27468,
27468,
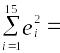 30.
30.
1.
Оцените коэффициенты линейной регрессии
![]() .
.
2. Определите стандартные ошибки коэффициентов.
3.
Вычислите
и
![]() .
.
4.
Оцените статистическую значимость
коэффициентов регрессии и детерминации
при уровне значимости
![]() =0,05.
=0,05.
Задача 4
Пусть определена регрессия
![]() ,
причем
,
причем
![]() .
При отбрасывании переменной
.
При отбрасывании переменной
![]() и оценке регрессии
коэффициент
и оценке регрессии
коэффициент
![]() оказался отрицательным
оказался отрицательным
![]() .
Возможно ли это? Если да, тогда при каких
обстоятельствах?
.
Возможно ли это? Если да, тогда при каких
обстоятельствах?
Задача 5
Докажите,
что график уравнения парной линейной
регрессии всегда проходит через точку
с координатами
![]() ,
где
,
где
![]() -
средние значения переменных
-
средние значения переменных
Вариант 2.
Задача 1.
Имеется информация о деятельности 10 компаний. -оборот капитала (млрд. руб.), - чистый доход (млрд.руб.):
№ п/п |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
X |
31,3 |
13,4 |
4,5 |
10,0 |
20,0 |
15,0 |
60,1 |
17,9 |
40,2 |
2,0 |
Y |
2,2 |
1,7 |
0,7 |
1,7 |
2,2 |
1,3 |
4,1 |
1,6 |
2,5 |
0,5 |
1. Оцените коэффициенты линейной регрессии по методу наименьших квадратов.
2. Проверьте статистическую значимость оценок теоретических коэффициентов при уровне значимости .
3. Рассчитайте 95%-е доверительные интервалы для теоретических коэффициентов регрессии.
4.
Спрогнозируйте чистый доход при обороте
капитала
![]() и рассчитайте 95% доверительный интервал
для условного математического ожидания
и рассчитайте 95% доверительный интервал
для условного математического ожидания
![]() .
.
5. Рассчитайте границы интервала, в котором будет сосредоточено не менее 95% возможных значений чистого дохода при обороте капитала .
6. Оцените на сколько изменится чистый доход, если оборот капитала вырастет на 3 млрд.руб.
7. Рассчитайте коэффициент детерминации .
8. Рассчитайте - статистику для коэффициента детерминации и оцените его статистическую значимость.
Задача 2.
Имеется информация за 15 лет относительно среднего дохода и среднего потребления (млн.руб.):
Годы |
X |
Y |
Годы |
X |
Y |
Годы |
X |
Y |
1995 |
10,5 |
8,8 |
2000 |
16,1 |
11,9 |
2005 |
23,1 |
20,5 |
1996 |
11,6 |
12,0 |
2001 |
17,3 |
13,5 |
2006 |
24,3 |
19,5 |
1997 |
12,3 |
13,0 |
2002 |
18,7 |
15,0 |
2007 |
25,5 |
19,1 |
1998 |
13,7 |
12,6 |
2003 |
20,1 |
18,2 |
2008 |
27,8 |
19,3 |
1999 |
14,5 |
11,2 |
2004 |
21,8 |
21,2 |
2009 |
30,0 |
24,0 |
