
ЗАДАНИЕ на контрольную работу
Требования:
Контрольная работа состоит из 3 разделов. Каждый раздел оформляется с нового листа. В контрольной работе приводится номер раздел, номер задания и подробное решение с необходимыми пояснениями.
Контрольная работа выполняется в печатной форме в соответствии с требованиями в методических указаниях по оформлению курсовых работ, курсовых и дипломных проектов (Учебные материалы\230102-АСОИУ\ДИПЛОМНОЕ ПРОЕКТИРОВАНИЕ)
К контрольной работе прикладывается лист рецензии.
Сдать контрольную работу необходимо за 1 неделю до начала сессии.
Вариант задания на контрольную работу соответствует порядковому номеру студента в списке группы.
|
ИВТ-13 ЗФО |
|
|
№п/п |
Фамилия |
Имя |
Отчество |
1 |
Горбунов |
Максим |
Александрович |
2 |
Воронова |
Ирина |
Александровна |
3 |
Вяткин |
Кирилл |
Андреевич |
4 |
Дулесов |
Роман |
Михайлович |
5 |
Кондаков |
Николай |
Владимирович |
6 |
Котов |
Никита |
Игоревич |
7 |
Лаврухина |
Анна |
Александровна |
8 |
Павлов |
Геннадий |
Владимирович |
9 |
Рулёв |
Александр |
Геннадьевич |
10 |
Смирнов |
Игорь |
Сергеевич |
11 |
Соколов |
Олег |
Юрьевич |
12 |
Троков |
Дмитрий |
Павлович |
Раздел 1
В-1
Какая формула называется тождественно-истиной? Доказать тождественную истинность формул:
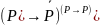
Найди минимальную дизъюнктивную нормальную форму формулы:
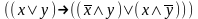
Привести к совершенной дизъюнктивной нормальной форме:
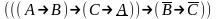
Найти все существенные переменные функции:
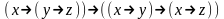
5. Являются ли системы функционально полными?
{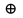 ,
~}
,
~}
Задать произвольную аксиоматическую теорию.
Доказать выводимость формулы АА в построенной аксиоматической теории.
Привести определение предиката, предметной области предиката.
Решить задачу: в области N = 0,1,2,… заданы предикаты
S=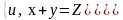 и Р=
и Р=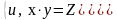
Записать выражение, область истинности которого задана отношением: х > у.
Составить ПНФ: х (Р(х) у(Р(у)((Q(x) Q(y))z Р(z)))).
В-2
Какая формула называется тождественно-ложной? Проверить, является ли формула тождественно-ложной:
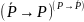
При каких значениях пропорциональных переменных, следующие формулы ложные:
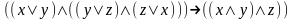
Привести к совершенной конъюнктивной нормальной форме:
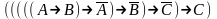
Найди минимальную дизъюнктивную нормальную форму формулы:
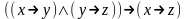
5. Являются ли системы функционально полными?
{ ,~}
,~}
Объяснить понятие: «полнота аксиоматической теории». Привести доказательство полноты построенной аксиоматической теории.
Дать определение МТ. Описать основные устройства МТ. Построить МТ для правильного вычисления функции у=2*х.
Привести доказательство клаузы конструктивным методом:
A(B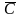 ),
), B,
(
B,
(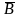 ®C)
C;B
®C)
C;B
В-3
Если формула не тождественно-ложная, то она тождественно-истинная? Доказать тождественную истинность формул:
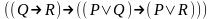
При каких значениях пропорциональных переменных, следующие формулы ложные:
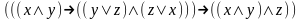
Привести к совершенной дизъюнктивной нормальной форме:
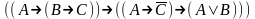
Найди минимальную дизъюнктивную нормальную форму формулы:
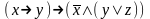
5. Являются ли системы функционально полными?
{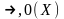 }
}
Привести алгоритм получения предваренной нормальной формы (ПНФ). Составить ПНФ:(х (А(х) В(у)) (х А(x) у В(у))).
Пусть М- множество, состоящее из других множеств и предикат Р(х,у)=и х у.
Записать, что х- есть пересечение у и z.
В-4
Может формула быть не тождественно-истинной и не тождественно-ложной одновременно? Доказать тождественную истинность формул:
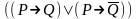
При каких значениях пропорциональных переменных, следующие формулы ложные:
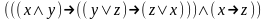
Привести к совершенной конъюнктивной нормальной форме :
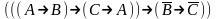
Найди минимальную дизъюнктивную нормальную форму формулы:
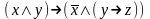
5. Являются ли системы функционально полными?
{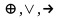 }
}
Определить понятия: примитивно-рекурсивное отношение, примитивно-рекурсивный предикат. Проверить, является ли предикат
Р=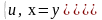
примитивно-рекурсивным.
Привести доказательство выводимости формулы
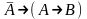 в построенной аксиоматической теории.
в построенной аксиоматической теории.
Составить ПНФ: (х у Р(х,у)ху(Р(x,у) Р(у,х))).
В-5
Какая формула называется тождественно-истиной? Является ли тождественно-ложной формула:
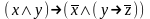
При каких значениях пропорциональных переменных, следующие формулы ложные:
Привести к совершенной дизъюнктивной нормальной форме:
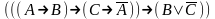
Найди минимальную дизъюнктивную нормальную форму формулы:
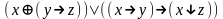
5. Являются ли системы функционально полными?
{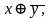 x
~y}
x
~y}
Объяснить понятие: «непротиворечивость аксиоматической теории». Привести доказательство непротиворечивости построенной аксиоматической теории.
Дать определение машины Тьюринга (МТ). Определить разновидности памяти МТ. Привести способы задания МТ. Построить МТ для сложения двух чисел.
в области N = 1,2,… заданы предикаты S= и Р=
Записать выражение, область истинности которого задана отношением: х = у.
В-6
Какая формула называется тождественно-ложной? Проверить, является ли формула тождественно-ложной:
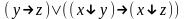
При каких значениях пропорциональных переменных, следующие формулы ложные:
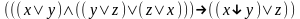
Привести к совершенной конъюнктивной нормальной форме:
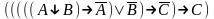
Найди минимальную дизъюнктивную нормальную форму формулы:
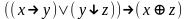
5. Являются ли системы функционально полными?
{х
y,
x~y,
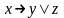 }
}
Привести основные конструкции клауз: тавтология, противоречие. Используя метод резолюций привести доказательство истинности клаузы: A®B,C®D,B®E,D®F,
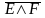 ,A®CÞ
,A®CÞ
Привести способы задания предиката. Пусть М- множество, состоящее из других множеств и предикат Р(х,у)=и х у. Записать, что х – дополнение у.
Построить машину Тьюринга, правильно вычисляющую функцию f(x)=|x-y|.
В-7
Если формула не тождественно-ложная, то она тождественно-истинная? Проверить тождественную истинность формул:
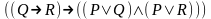
При каких значениях пропорциональных переменных, следующие формулы ложные:
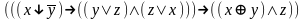
Привести к совершенной дизъюнктивной нормальной форме:
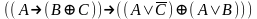
Найди минимальную дизъюнктивную нормальную форму формулы:
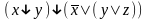
5. Являются ли системы функционально полными?
{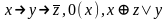 }
}
Привести определения: булева функция, предикат. В чем отличие понятий? Пусть задан предикат Р=и у=1/х. Указать его область истинности. Построить МТ для правильного вычисления предиката.
Доказать следующие замечания:
А)если Ф(х1, х2, …, хn) – не тождественно-ложная формула, то она выполнима.
Б) если формула Ф(х1, х2, …, хn) – общезначима, то она выполнима.
Построить машину Тьюринга, правильно вычисляющую функцию (х у), где «» -знак урезанной разности.
В-8
Может формула быть не тождественно-истинной и не тождественно-ложной одновременно? Проверить тождественную истинность формул:
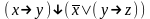
При каких значениях пропорциональных переменных, следующие формулы ложные:
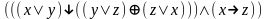
Привести к совершенной конъюнктивной нормальной форме :
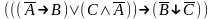
Найди минимальную дизъюнктивную нормальную форму формулы:
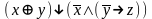
Являются ли системы функционально полными?
{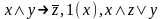 }
}
Определить понятия: тождественно-ложная формула, равносильные формулы логики предикатов. Является ли тождественно-истинной формула хР(х) хР(х). Привести содержательный пример.
Привести схему конструктивного метода доказательства. Проверить истинность клаузы, используя конструктивный метод: E®F,C®(D®E),(A®B) ®CÞD®(
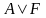 ).
). в области N = 0,1,2,… заданы предикаты
S= и Р=
Представить высказывание «любое число можно представить в виде суммы квадратов двух других чисел» в предикатной форме.
В-9
Какая формула называется тождественно-истиной? Проверить тождественную истинность формул:
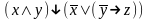
При каких значениях пропорциональных переменных, следующие формулы ложные:
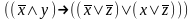
Привести к совершенной дизъюнктивной нормальной форме:
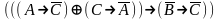
Найди минимальную дизъюнктивную нормальную форму формулы:
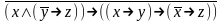
5. Являются ли системы функционально полными?
{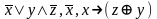 }
}
Задать смысл кванторов, пояснить на примерах. Дать определение связанной и свободной переменной. Доказать х Р(х) х ( Р(х)) и привести содержательный пример.
Привести определение МТ, правильно вычисляющей функцию. Построить МТ для правильного вычисления функции у=2х.
Составить клаузу и проверить ее на противоречивость. Уменьшение температуры приводит к снижению давления и уменьшению объема. Увеличение объема приводит к росту скорости потока. Повышение давления приводит к падению уровня, если при этом уменьшать температуру. Снижение скорости приводит к уменьшению давления или росту температуры. Технолог Иванов рассудил так: мне надо повысить давление при одновременном снижении скорости потока, поэтому я должен увеличить объем и температуру.
В-10
Какая формула называется тождественно-ложной? Доказать тождественную истинность формул:
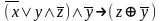
При каких значениях пропорциональных переменных, следующие формулы ложные:

Привести к совершенной конъюнктивной нормальной форме:
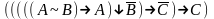
Найди минимальную дизъюнктивную нормальную форму формулы:
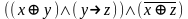
Являются ли системы функционально полными?
{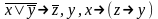 }
}
Определить понятие тождественно-истинной формулы в широком смысле. Доказать, что, если формула Ф(х1 ,х2 , … хn) не тождественно-истинна в широком смысле, то найдется такая модель и набор переменных из данной модели, на которых Ф(х1 ,х2 , … хn) – ложна. Привести содержательный пример.
Построить машину Тьюринга, правильно вычисляющую функцию (1 у), где «» -знак урезанной разности.
Построить машину Тьюринга, правильно вычисляющую функцию
f(x,y)
=

В-11
Если формула не тождественно-ложная, то она тождественно-истинная? Проверить тождественную истинность формул:
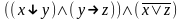
При каких значениях пропорциональных переменных, следующие формулы ложные:
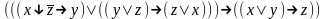
Привести к совершенной дизъюнктивной нормальной форме:
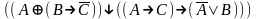
Найди минимальную дизъюнктивную нормальную форму формулы:
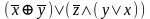
5.Являются ли системы функционально полными?
{ }
}
Определить понятия: общезначимой формулы в данной модели и формулы, выводимой в данной модели. В чем их различие? Привести примеры к каждому определению.
Задать определения: МТ, правильно вычисляющей предикат; МТ, вычисляющая предикат с восстановлением. Построить МТ для правильного вычисления предиката:
Р=
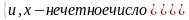
Составить ПНФ: х (у(Р(х,у) у(Р(у,х))у((Q(x,у)Q(y,х))z Р(z)).
В-12
Может формула быть не тождественно-истинной и не тождественно-ложной одновременно? Проверить тождественную истинность формул:
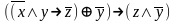
При каких значениях пропорциональных переменных, следующие формулы ложные:

Привести к совершенной конъюнктивной нормальной форме :
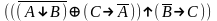
Найди минимальную дизъюнктивную нормальную форму формулы:
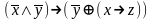
5. Являются ли системы функционально полными?
{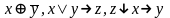 }
}
Привести определение равносильных формул. Доказать равносильность следующих формул и привести к ним содержательные примеры:
А) х Р(х) х ( Р(х)).
Б) х Р(х) х ( Р(х)).
Построить машину Тьюринга, правильно вычисляющую функцию
f(x)
=
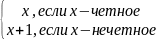
Построить клаузу и проверить ее истинность: увеличение денег в обращении влечет за собой инфляцию. Но рост денежной массы происходит по двум причинам: из-за денежной эмиссии или снижения товарооборота. Снижение товарооборота приводит к безработице и спаду производства. Из-за инфляции падает курс денежной единицы. Рекомендации экономиста Иванова: увеличить денежную эмиссию и поднять производство, тогда избежим безработицы, и курс денежной единицы останется без изменения.
