1)Модель –– это материальный или идеальный объект, замещающий исследуемую систему и адекватным образом отображающий ее существенные стороны. Модель должна в чем–то повторять исследуемый процесс или объект со степенью соответствия, позволяющей изучить объект–оригинал . Чтобы результаты моделирования можно было бы перенести на исследуемый объект, модель должна обладать свойством адекватности. Модель объекта должна отражать его наиболее важные качества, пренебрегая второстепенными. Выделяют следующие виды моделей: 1) детерминированные и стохастические; 2) статические и динамические; 3) дискретные, непрерывные и дискретно–непрерывные; 4) мысленные и реальные. В других работах модели классифицируют по следующим основаниям по характеру моделируемой стороны объекта; 2) по отношению ко времени; 3) по способу представления состояния системы; 4) по степени случайности моделируемого процесса; 5) по способу реализации. Компьютерная модель - это модель реального процесса или явления, реализованная компьютерными средствами.

Компьютерные модели, как правило, являются знаковыми или информационными. К знаковым моделям в первую очередь относятся математические модели, демонстрационные и имитационные программы.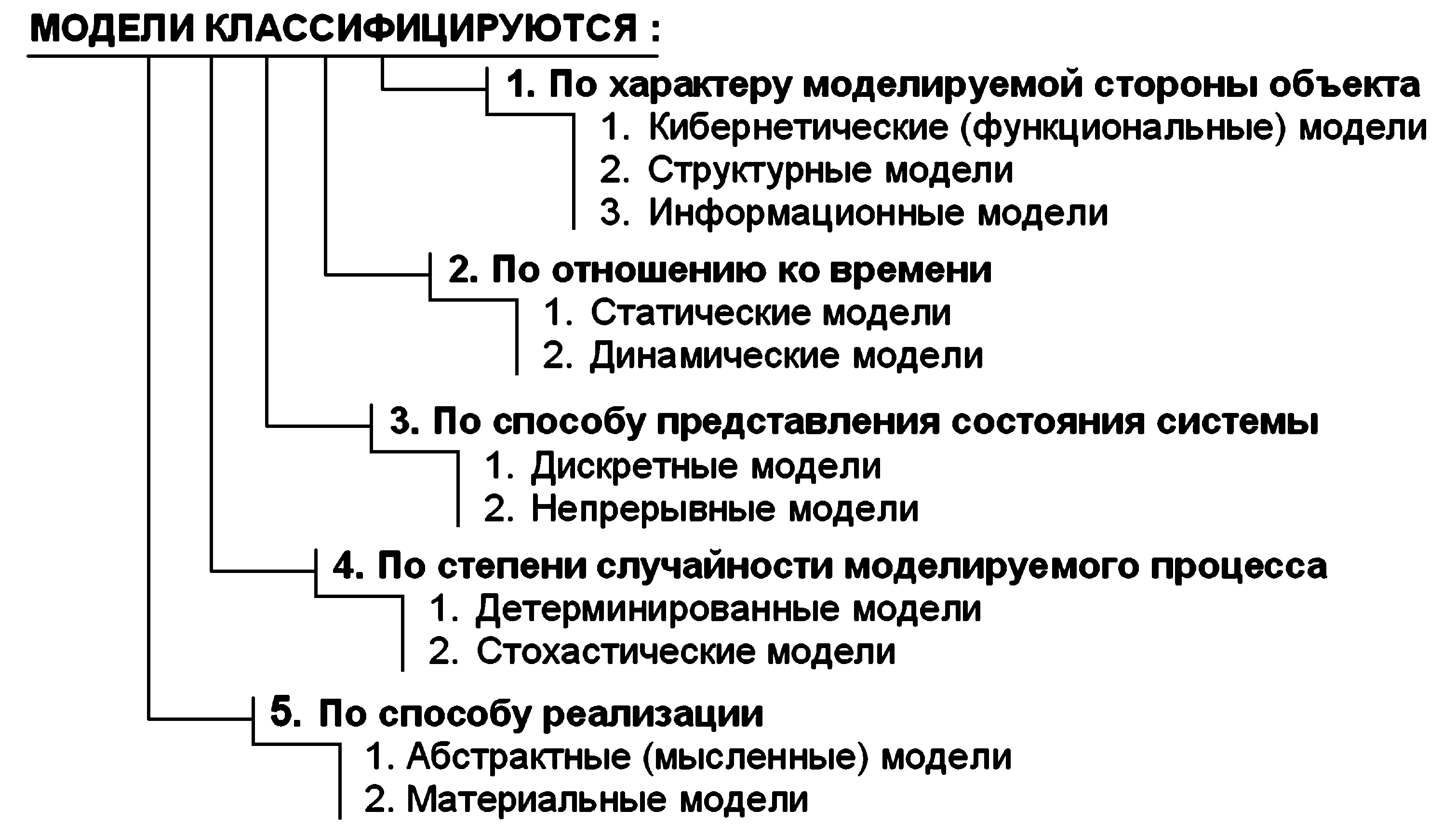

Требования: Первым таким требованием является ее ингерентность, то есть достаточная степень согласованности создаваемой модели со средой. Второе требование – простота модели. третье требование, предъявляемое к модели – ее адекватность. Адекватность модели означает возможность с ее помощью достичь поставленной цели проекта в соответствии со сформулированными критериями. Адекватность модели означает, что она достаточно полна, точна и истинна. Формализация информации о некотором объекте – это ее отражение в определенной форме. Можно еще сказать так: формализация — это сведение содержания к форме. Формулы, описывающие физические процессы, — это формализация этих процессов. Радиосхема электронного устройства — это формализация функционирования этого устройства. Ноты, записанные на нотном листе, — это формализация музыки .Формализованная информационная модель — это определенные совокупности знаков (символов), которые существуют отдельно от объекта моделирования, могут подвергаться передаче и обработке. Реализация информационной модели на компьютере сводится к ее формализации в форматы данных, с которыми "умеет" работать компьютер.

2) Информационное моделирование – это творческий процесс. Не существует универсального рецепта построения моделей, пригодного на все случаи жизни, но можно выделить основные этапы и закономерности, характерные для создания самых разных моделей.ЭТАПЫ:1-Описательная информационная модель. На первом этапе исследования объекта или процесса обычно строится описательная информационная модель. Такая модель выделяет существенные, с точки зрения целей проводимого исследования, параметры объекта, а несущественными параметрами пренебрегает.2-Формализованная модель. На втором этапе создается формализованная модель, т. е. описательная информационная модель записывается с помощью какого-либо формального языка. В такой модели с помощью формул, уравнений или неравенств фиксируются формальные соотношения между начальными и конечными значениями свойств объектов, а также накладываются ограничения на допустимые значения этих свойств.3-Компьютерная модель. На третьем этапе необходимо формализованную информационную модель преобразовать в компьютерную модель, т. е. выразить ее на понятном для компьютера языке. Существуют различные пути построения компьютерных моделей, в том числе:- создание компьютерной модели в форме проекта на одном из языков программирования; построение компьютерной модели с использованием электронных таблиц или других приложений: систем компьютерного черчения, систем управления базами данных, геоинформационных систем .4-Компьютерный эксперимент. Четвертый этап исследования информационной модели состоит в проведении компьютерного эксперимента. Если компьютерная модель существует в виде проекта на одном из языков программирования, ее нужно запустить на выполнение, ввести исходные данные и получить результаты. Если компьютерная модель исследуется в приложении, например в электронных таблицах, то можно построить диаграмму или график, провести сортировку и поиск данных или использовать другие специализированные методы обработки данных.5-Анализ полученных результатов и корректировка исследуемой модели. Пятый этап состоит в анализе полученных результатов и корректировке исследуемой модели. В случае несоответствия результатов, полученных при исследовании информационной модели, измеряемым параметрам реальных объектов можно сделать вывод, что на предыдущих этапах построения модели были допущены ошибки или неточности.

3) Источники и классификация погрешности.Погрешность решения задачи обуславливается следующими причинами:

1) математическое описание задачи является неточным, в частности неточно заданы исходные данные описания; 2) применяемый для решения метод часто не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций; поэтому вместо точного решения задачи приходится прибегать к приближенному; 3) при вводе данных в машину, при выполнении арифметических операций и при выводе данных производятся округления.

Погрешности, соответствующие этим причинам, называют: 1) неустранимой погрешностью, 2) погрешностью метода, 3) вычислительной погрешностью.

Часто неустранимую погрешность подразделяют на две части: а) неустранимой погрешностью называют лишь погрешность, являющуюся следствием неточности задания числовых данных, входящих в математическое описание задачи; б) погрешность, являющуюся следствием несоответствия математического описания задачи реальности, называют, соответственно, погрешностью математической модели. Погрешности приближенных вычислений

Понятие о погрешности приближенияЕстественно, что приближенное и точное число всегда отличаются друг от друга. Иначе говоря, при приближении возникает некоторая погрешность приближения. Причем, в математике различают относительную и абсолютную погрешность.

Абсолютной погрешностью (или, просто, погрешностью) приближенного числа называют разность между этим числом и его точным значением (при этом из большего числа вычитается меньшее) .Пример

При округлении числа 1284 до 1300 абсолютная погрешность составляет 1300-1284=16. А при округлении до 1280 абсолютная погрешность составляет 1280-1284 = 4.

Относительной погрешностью приближенного числа называется отношение абсолютной погрешности приближенного числа к самому этому (точному) числу.Пример

При округлении числа 197 до 200 абсолютная погрешность составляет 200-197 = 3. Относительная погрешность равна 3/197 ≈ 0,01523 или приближенно 3/200 ≈ 1,5%.

Значащей цифрой приближённого числа называется всякая цифра в его десятичном изображении, отличная от нуля, и нуль, если он содержится между значащими цифрами или является представителем сохранённого десятичного разряда. Все остальные нули, входящие в состав приближённого числа и служащие лишь для обозначения его десятичных разрядов, не причисляются к значащим цифрам.

31) Моделирование случайных величин. Для формирования последовательности случайных чисел в компьютере может использоваться один из трех основных способов: аппаратный (физический); табличный (файловый); алгоритмический (программный).

Аппаратный способ. При этом способе случайные числа формируются специальным устройством. Источником случайных чисел чаще всего являются шумы в электронных приборах. Временные расстояния между шумовыми всплесками, превышающими подобранный уровень ограничения, фиксируются как случайные числа из распределения \gamma \sim Rav[0, 1].

Преимущества такого способа: количество случайных чисел неограниченно; не требует затрат оперативной памяти; требует малые вычислительные ресурсы компьютера.Недостатки, которые в настоящее время исключили его из инженерной практики: трудность настройки; необходимость периодической проверки формируемой последовательности на соответствие закону распределения;обеспечение стабильности условий работы устройства - питания, влажности, температуры, старения приборов и элементов; при необходимости невозможно повторить эксперимент при одной и той же последовательности случайных чисел.

Табличный способ. Случайные числа в виде таблицы (файла) помещаются в оперативную или внешнюю память компьютера. Эти числа формируются заранее или берутся из соответствующего справочника. Достоинствами такого способа являются:числа требуют однократную проверку при формировании или недоверии источнику;можно повторять вычислительный эксперимент при одной и той же последовательности случайных чисел.Недостатки же: количество случайных чисел ограничено; файл занимает место в оперативной памяти компьютера; при размещении во внешней памяти обращение за случайными числами увеличивает время моделирования.

Алгоритмический способ. При этом способе случайные числа формируются с помощью специальных алгоритмов (формул) и реализующих их программ при каждом обращении моделирующего алгоритма за случайным числом. Достоинства способа:в настоящее время предлагается достаточно алгоритмов, генерирующих случайные числа, проверенных практикой и, следовательно, не нуждающихся в особых проверках; можно многократно воспроизвести одну и ту же последовательность; в памяти компьютера хранится только программа датчика (генератора), занимающая, как правило, малый объем; алгоритмический датчик может быть реализован и аппа-ратно, за счет чего существенно сокращается время формирования случайного числа и в целом время моделирования.Недостатки: на формирование случайного числа при программной реализации датчика требуются затраты машинного времени; любой алгоритмический датчик может сгенерировать ограниченное количество неповторяющихся чисел.

Требования к датчику случайных чисел.Прежде чем перейти к описанию конкретных алгоритмов получения на ЭВМ последовательностей псевдослучайных чисел, сформулируем набор требований, которым должен удовлетворять идеальный генератор. Полученные с помощью идеального генератора псевдослучайные последовательности чисел должны состоять из квазиравномерно распределенных чисел, содержать статистически независимые числа, быть воспроизводимыми, иметь неповторяющиеся числа, получаться с минимальными затратами машинного времени, занимать минимальный объем машинной памяти.

32) Метод серединных квадратов.Пусть имеется 2n-разрядное число, меньшее 1.Возведем его в квадрат

'а затем отберем средние 2n разрядов, которые и будут являться очередным чис­лом псевдослучайной последовательности

Этому методу соответствует рекуррентное соотношение

(2) где В [ • ] и Ц [ • ] означают соответственно дробную и целую часть числа в квадратных скобках.

Недостаток метода - наличие корреляции между числами последовательности, а в ряде случаев случайность вообще может отсутствовать. Кроме того, при не­которых i* может наблюдаться вырождение последовательности, т.е. xi = 0 при i ³ i*.

Мультипликативный метод

Широкое применение для получения последовательностей псевдослучайных равномерно распределенных чисел получили конгруэнтные процедуры генерации, которые могут быть реализованы мультипликативным либо смешанным методом.

Алгоритм построения последовательности для двоичной машины М = рg сво­дится к выполнению следующих операций:

1-выбрать в качестве Х0 произвольное нечетное число;2) вычислить коэффициент , где l - любое целое положительное число;3) найти произведение l Х0, содержащее не более 2g значащих разрядов;4) взять g младших разрядов в качестве первого числа последовательности X1, а остальные отбросить;5) определить дробь из интервала (0, 1 );6) присвоить Х0 = X1;7) вернуться к пункту 3.

33)В настоящее время все языки высокого уровня имеют программные генераторы равномерно распределенных последовательностей псевдослучайных чисел. Их называют датчиками случайных чисел. Датчики случайных чисел, как правило имеют имена: RAN, RAND, RANDU, RND, RANDOM, RANDOMIZE и т.д. Эти имена получены от английского слова random, означающего случайный или выбранный наугад. Поэтому датчики случайных чисел иногда называют рандомизаторами.Датчики случайных чисел обычно генерируют последовательность действительных чисел Un, равномерно распределенных между нулем и единицей, т.е. последовательность случайных дробей в интервале [0,1]. Но вначале датчики генерируют последовательность целых случайных чисел xi в интервале от нуля до m, где m – размер машинного слова (на единицу меньше максимального целого числа, размещающегося в машинном слове).

Алгоритм датчика randu

34) Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями.

Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями.

Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически.Для моделирования значений дискретной случайной величины x разделим единичный интервал [0; 1] на n непересекающихся отрезков длиной D_i = p_i

Теорема: Случайная величина x , определенная соотношением ( 4.1 )x = хi , если g Î Di , ( 4.1 )

имеет заданный закон распределения, представленный в виде ряда распределения:

Доказательство. Рассмотрим вероятности:

Р {x = xi} = P {g Î Di} = длина Di = pi ,ЧТД

35) Моделирование непрерывных случайных величинВ данном случае используется метод обратной функции. Пусть есть некоторая функция распределения случайной величины .Разыграем на оси ординат точку r, используя функцию F(х). Тогда можем получить значение величины Х такое, что F(x)=r.

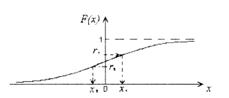
Найдем функцию распределения F(x) случайной величины X. По определению она равна вероятности P(X<x). Из рисочевид­но, что

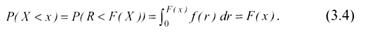
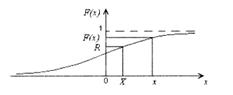
Таким образом, последовательность r1, r2, r3, ... , принадлежащая R(0,1), преобразуется в последовательность x1, х2, x3,…, которая име­ет заданную функцию плотности распределения f(x).

Моделирование равномерного распределения в интервале (a, b) случайной величины. Для моделирования воспользуемся ме­тодом обратной функции. На рис. 3.8 показана функция плотности равномерного распределения.

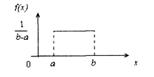
Находим функцию распределения и приравниваем ее к случай­ному числу

Отсюда Х = (b – a)R + а.

Моделирование экспоненциального распределения случай­ной величины. Функция плотности экспоненциального распределе­ния случайной величины f(x) = и функция распределения пока­заны на рис. 1.1.