§2.2. Різні види збіжності послідовності функцій та зв’язок між ними.

Нехай – простір із мірою , визначеною на -алгебрі , .

Із попереднього параграфа випливає, що сукупність всіх вимірних функцій виду замкнута відносно арифметичних дій над ними. Виявляється, що ця сукупність замкнута також відносно поняття збіжності послідовності функцій із цієї сукупності, тобто, якщо послідовність вимірних функцій поточково (в кожній точці із ) збігається на множині до функції , 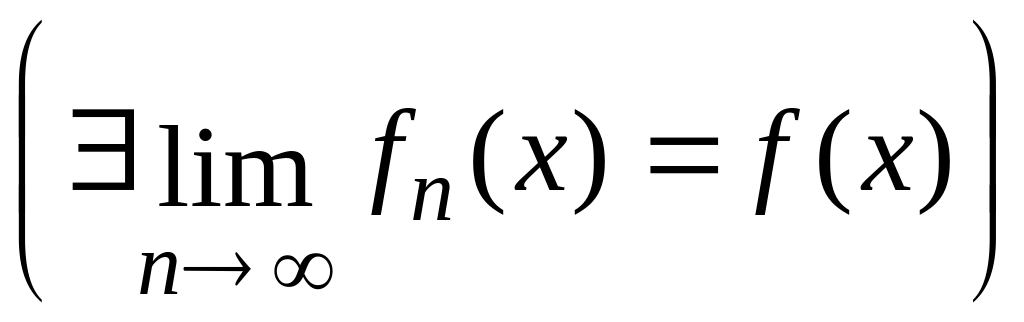, то функція вимірна.

Для послідовності вимірних функцій можна розглядати, окрім поточкової збіжності ще наступні види збіжності: рівномірну збіжність на множині , збіжність майже скрізь на , збіжність за мірою на .

Говорять, що послідовність вимірних функцій до функції збігається:

1. рівномірно на множині , якщо 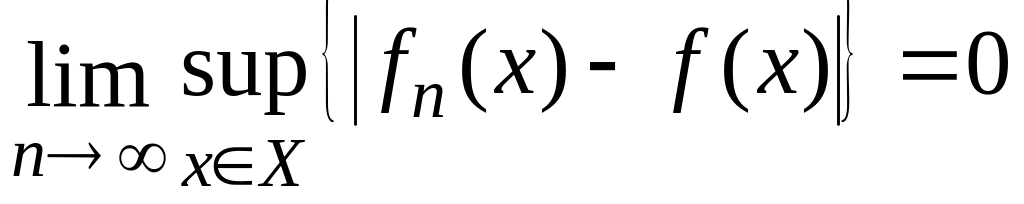(таку збіжність записують у вигляді );

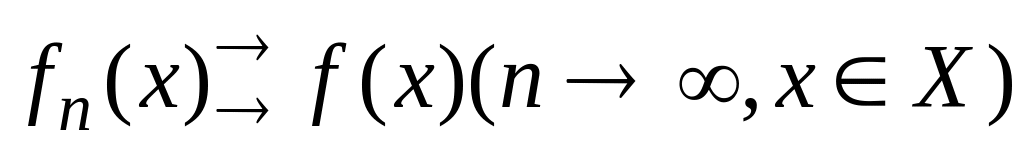2. майже скрізь на множині відносно міри , якщо для всіх точок х із Х за виключенням, можливо, точок із деякої множини міри нуль (таку збіжність записують у вигляді )

Говорять, що послідовність вимірних функцій збігається на множині за мірою до вимірної функції , якщо для кожного , де (таку збіжність записують у вигляді )

Якщо послідовність вимірних функцій така, що і міра повна, то як можна показати функція f вимірна на .

Вказані вище види збіжності пов’язані між собою. Зрозуміло, що з рівномірної збіжності на множині послідовності вимірних на функцій випливає її поточкова збіжність і, отже, її збіжність майже скрізь на множині та збіжність за мірою на . Більш тонкі зв’язки між вказаними видами збіжності розкривають наступні теореми А. Лебега, Ф.Рісса, Д. Єгорова.

Теорема А. Лебега. Якщо послідовність вимірних функцій збігається майже скрізь на множині , ,до вимірної функції , тобто ,то вона збігається до функції і за мірою тобто .

Зафіксувавши довільне число , , розглянемо множини , . Очевидно, при кожному множини та є -вимірні і , множина є також -вимірна. Тоді, внаслідок неперервності міри ,

(1)

Окрім того при кожному

.

Тому є множина всіх тих точок із для яких числова послідовність не є збіжною до . Тому і, внаслідок (1), . Оскільки , то і . Отже, послідовність збігається за мірою на до .

Теорема Д. Єгорова. Якщо послідовність вимірних функцій , збігається майже скрізь на до функції ,то для кожного існує така вимірна множина , що і .

Скористаємося позначеннями з доведення попередньої теореми. При доведенні теореми А. Лебега було показано, що

(2)

при кожному , якщо збігається майже скрізь на до функції . Покладемо . Тоді із (2) випливає, що для заданого числа

.

Позначимо і покажемо, що є шукана множина з формулювання теореми Д. Єгорова. Справді, -вимірна множина і .

Далі, якщо то і тому , внаслідок законів де Моргана. Звідси випливає, що . А це означає, що , тобто .

Теорема Ф. Рісса. Якщо послідовність вимірних функцій збігається до функції за мірою , , то існує така підпослідовність цієї послідовності, що збігається майже скрізь на множині до функції тобто .

Знову використаємо всі позначення із доведення теореми А. Лебега. Задамо довільне число , . Із співвідношення випливає, що .

Отже, .

Позначивши дістанемо .

Отже, . Покажемо, що . Маємо

(3)

Якщо така точка із , що , то

. Отже, вказана точка належить множині . Оскільки то .