§1.11 Канторові множини

Сегмент точками розділимо на 3 частини однакової довжини. Вилучивши із сегмента середній інтервал , дістанемо об’єднання двох сегментів , . Сегмент точками , а сегмент точками розділимо знову на три частини однакової довжини. Вилучивши із вказаних сегментів середні інтервали

, дістанемо об’єднання 4 сегментів , , , . Кожен із останніх сегментів знову розділимо на 3 частини однакової довжини і вилучимо середні інтервали. І так далі. Продовжуючи цей процес до нескінченності, дістанемо певну множину , що утворюється із шляхом вилучення з нього зчисленної сукупності інтервалів , , , … Множина називається канторовою множиною. Множина , також називається канторовою множиною. Очевидно, . Зрозуміло, що множина не включає жодного сегмента як завгодно малої довжини. Множина є відкрита, як об’єднання зчисленної сукупності інтервалів, що попарно не перетинаються. Тому множина є замкнута, як доповнення відкритої множини до сегмента . Оскільки множини та є відповідно замкнута і відкрита , то вони вимірні за Лебегом, як множини на числовій прямій.

Множина є об’єднання 1 інтервала першого рангу (який вилучається із на першому кроці його поділу), двох інтервалів другого рангу (які викидаються із сегментів , на другому кроці при їх поділу) і т. д. Оскільки множина включає інтервалів n-го рангу, довжина кожного з яких дорівнює , то лінійна міра Лебега множини обчислюється наступним способом

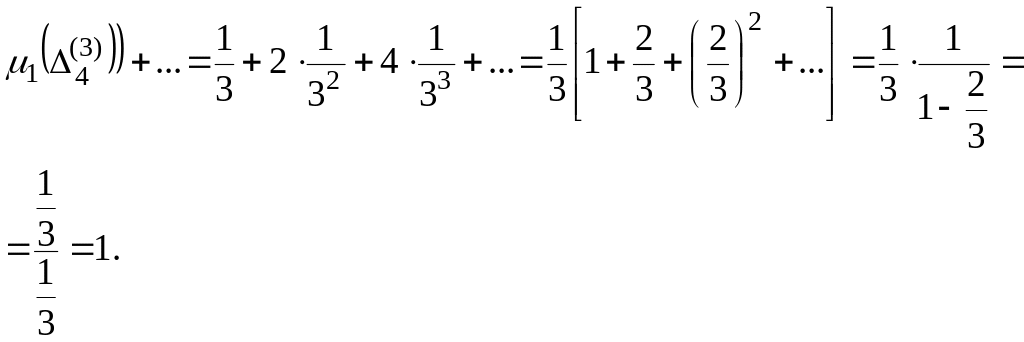Оскільки , то . Таким чином канторова множина має лебегову міру рівну нулю, .

До множини належать всі кінці вилучених із інтервалів. Тому ця множина не менш ніж зчисленна за потужністю. Однак, справедливе наступне твердження.

Теорема. Множина Кантора має потужність континуума.

Припустимо протилежне до твердження теореми тобто, що множина є зчисленна. Тоді її можна записати у вигляді

, де при . (1)

Позначимо через той із двох сегментів першого рангу , , який не містить точку , ; позначимо через , той із чотирьох сегментів другого рангу, що включаються в , який не містить точку , . І так далі.

Продовжуючи цей процес до нескінченності, дістанемо послідовність сегментів таку, що і при цьому не містить точок . Оскільки крім того має довжину , то згідно з лемою про стяжні сегменти, сегменти послідовності мають і причому єдину спільну точку , яка не є елементом послідовності (1), що суперечить нашому припущенню. Одержане протиріччя і показує справедливість теореми.

Зауваження. Із доведеної теореми випливає, що канторова множина окрім кінців інтервалів, що вилучаються із при її утворенні, містить ще й інші точки, бо в протилежному випадку вона була б лише зчисленною.

Розділ II. Вимірні функції та їх властивості.

2.1. Поняття вимірної функції. Еквівалентні функції.

Нехай – довільна непорожня множина і – -алгебра множин, . Тоді впорядкована пара називається вимірним простором, а множини із називаються вимірними. Якщо при цьому є міра на , то впорядкована трійка називається простором із мірою.

Нехай та – вимірні простори. Тоді відображення називається – -вимірним, якщо . При цьому, якщо , , то – – -вимірне відображення називається -вимірним. Отже, можна сформулювати наступне означення.

Означення 1. Нехай – вимірний простір і – сігма-алгебра борелевих множин на . Тоді функція (відображення) називається -вимірною, якщо .

Очевидно, коли функція є -вимірна, то множина вимірна тобто і кожна функція , де , , є також -вимірна.

Зазначимо, що множини , , , , де – довільне дійсне число називаються лебеговими множинами функції (відображення) .

Попереднє означення, як можна показати, еквівалентне наступному означенню.

Означення 2. Функція називається -вимірною, якщо .

Очевидно, дістанемо рівносильні до попереднього означення, якщо в ньому замість взяти будь-яку іншу лебегову множину.

Якщо – простір із мірою , визначеною на -алгебрі , , то -вимірна функція називається інакше -вимірною або вимірною. Зокрема, якщо – сігма-алгебра всіх множин, вимірних за Лебегом, і , то -вимірна функція називається інакше вимірною за Лебегом.

Очевидно, в загальному випадку функція , що визначена на вимірній множині є –вимірна. Можна також показати, що композиція є вимірна функція, коли функція є -вимірна, а функція , де , неперервна. На основі цього доводиться, що функції , ( = const) є -вимірні на множині , якщо є -вимірна функція на . Можна також показати, що є -вимірні функції на множині , якщо функції , є – –вимірні на (при розгляді частки функцій додатково вимагається, щоб при ).

Можна показати, що функція , , вимірна за Лебегом, якщо вона неперервна на вимірній за Лебегом множині .

Нехай – простір із мірою , визначеною на -алгебрі , . Нехай і – така властивість, що кожен елемент із або володіє нею або не володіє. Тоді говорять, що властивість виконується майже скрізь на множині відносно міри , якщо множина не володіє властивістю вимірна, , і . Той факт, що властивість виконується майже скрізь на множині відносно міри записують: або .

Означення3. При вказаних вище умовах функції , де , називають еквівалентними на множині відносно міри (або еквівалентними), якщо і або інакше, коли . Той факт, що функції та еквівалентні будемо записувати .

Очевидно, коли міра повна, функція , , є вимірна і , то функція є також вимірна.