§1.7 Стандартне продовження міри із півкільця на -алгебру.

Нагадаємо, що функція , називається продовженням (поширенням) функції із класу множин , на клас множин , якщо і . При цьому функція називається звуженням функції із класу на клас і пишуть .

Якщо дано міру , визначену на півкільці , то зразу ж виникає питання про можливість продовження її з півкільця на більш широкий клас множин.

Теорема1. Міра , яка визначена на півкільці , завжди може бути продовжена причому єдиним способом із півкільця до міри визначеної на кільці і таке продовження здійснює міра , яка задається за допомогою формули

, (1)

де - довільна множина з , що записана у вигляді

, (2)

тобто при вказаних умовах . При цьому міра скінченна ( -скінченна), якщо міра скінченна ( -скінченна).

Спочатку зазначимо, що означення міри за допомогою рівності (1) коректне, тобто значення не залежить від запису множин , у вигляді (2). Окрім того із самої рівності (1) випливає, що функція невід’ємна і скінченно-аддитивна на . Покажемо, що функція є зчисленно-аддитивна. Нехай , причому . Множини та можна записати у вигляді

.

Оскільки функція скінченно-аддитивна, то

,

внаслідок того, що . Тому

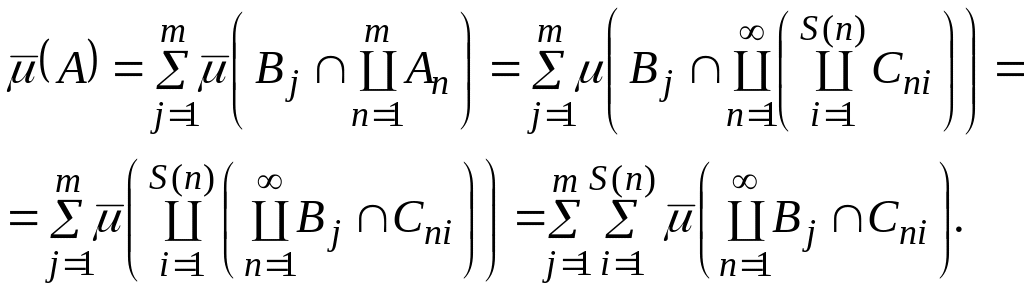
Очевидно, і на . Оскільки міра на є -аддитивна функція, то . Тому

Отже, -зчисленно-аддитивна міра, що визначена на . Єдиність продовження міри із на доводиться методом від протилежного.

Зауважимо, що перше твердження попередньої теореми справедливе і для скінченно-аддитивної міри на півкільці (тоді є також скінченно-аддитивна міра на ).

Подальше продовження міри (на ширший ніж клас множин) можна здійснити за допомогою поняття зовнішньої міри.

Якщо є довільна зовнішня міра, то як випливає з теореми Каратеодорі, клас усіх -вимірних множин є -алгебра множин із одиницею . Однак, ця -алгебра може виявитися порівняно вузькою – можливо, що , оскільки ця обставина залежить від . Виявляється, що у випадку, коли є зовнішня міра, яка породжена мірою , визначеною на півкільці , то -алгебра є достатньо широкий клас множин, який включає та . При цьому справедливе наступне твердження.

Теорема2. Якщо є міра на півкільці , і є зовнішня міра, що породжена мірою і є міра, яка породжена зовнішньою мірою , то міра є продовження міри із півкільця на -алгебру , , всіх -вимірних множин, тобто , і .

Нам достатньо показати, що ,оскільки тоді рівність , буде випливати зі співвідношень . Оскільки міру можна єдиним способом продовжити з півкільця на кільце , то в формулюванні теореми можна вважати, що - кільце множин.

Нехай . Зафіксуємо число . Візьмемо довільну множину , таку, що . З означення зовнішньої міри , породженої мірою визначеною на півкільці , випливає, що існує така послідовність множин із , що і . Враховуючи знову означення зовнішньої міри, породженої мірою на півкільці (у нас на кільці) та скінчену аддитивність міри на , дістаємо

.

Переходячи тут до границі при , дістанемо

.

Остання нерівність справедлива і коли .

Оскільки справедлива нерівність, що протилежна до попередньої нерівності, то .

Отже, множина , є -вимірна, тобто . Зрозуміло, що .

Означення. Міра із попередньої теореми називається стандартним продовженням (продовженням за Каратеодорі) міри із півкільця на -алгебру , а -вимірні множини при цьому називається -вимірними.

Якщо є довільна міра на півкільці , -зовнішня міра, що породжена мірою , то, як можна показати

,

де – -алгебра всіх -вимірних ( – вимірних) множин.

Як випливає із попереднього, стандартне продовження довільної міри із півкільця , на -алгебру , , є повна міра.

Можна показати, що продовження довільної -скінченної міри із кільця , на - кільце єдине і -скінчене.

Якщо є зовнішня міра, що породжена мірою , яка визначена на півкільці , і , то, як можна показати, , де – -алгебра усіх -вимірних множин. Іншими словами, при вказаних умовах множина , є -вимірна тоді і лише тоді, коли її з будь-якою точністю можна “наблизити” множинами із . Сукупність , усіх -вимірних множинах таких, що , утворює -кільце. Множина , , є -вимірна тоді і лише тоді, коли . Якщо міра , окрім того, –скінченна, то , де ( ). В цьому випадку, як можна показати, множина , , є –вимірна тоді і лише тоді, коли ( , причому .