§1.5 Неперервність міри.

Часто використовується властивість неперервності міри, сутність якої розкриває наступне твердження.

Теорема (про неперервність міри). Міра , що визначена на кільці , є неперервна функція, тобто справедливі твердження:

1. ;

2. .

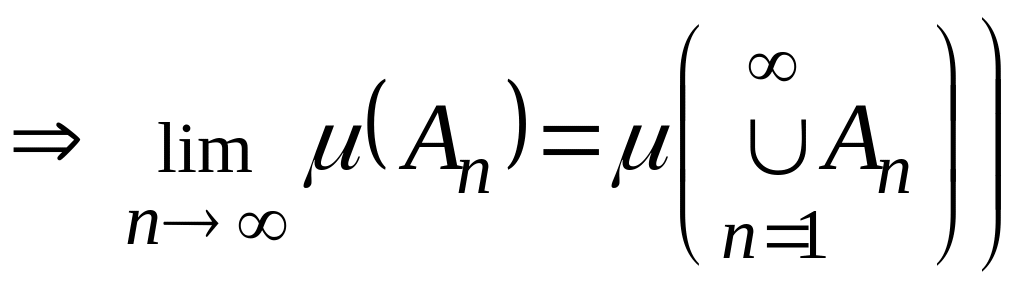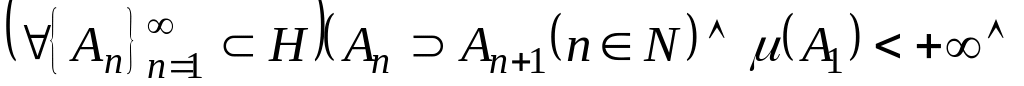
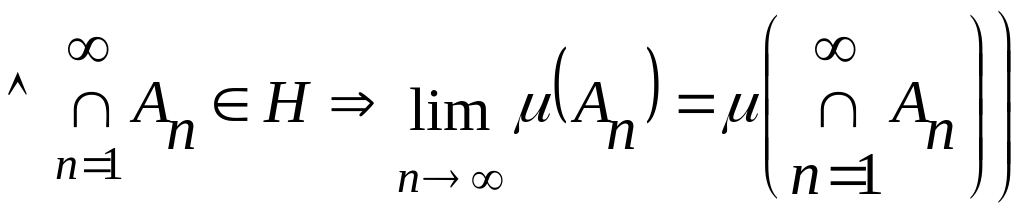Нехай - довільна послідовність множин з кільця , що задовольняє умови: і . Якщо , то в силу монотонності міри на буде .

Отже, тобто справедливе твердження 1). Якщо , то в силу –аддитивності міри дістанемо

тобто знову справедливе твердження 1).

Аналогічно доводиться твердження 2) .

§1.6 Зовнішня міра та міра породжена нею. Поняття вимірної множини.

Виявляється, що міру можна побудувати на основі більш широкого поняття, яким є поняття зовнішньої міри.

Означення 1. Функція , де - довільна непорожня множина, називається зовнішньою мірою, якщо виконуються умови:

1)

2) ;

3) .

Зауважимо, що із останньої вимоги випливає

, а також монотонність зовнішньої міри тобто твердження .

Часто використовується зовнішня міра, що побудована наступним способом. Якщо , є міра, що задана на півкільці , то розглянемо функцію таку, що =0, , якщо існує принаймні одне покриття множини , зчисленною сукупність множин із (точна нижня межа відшукується від сукупності сум , які відповідають вказаним покриттям множини ), і , якщо не існує жодного покриття множини , вказаного вище. Можна показати, що функція , побудована вказаним способом, є зовнішня міра. Вона називається зовнішньою мірою породженою мірою , визначеною на півкільці . Ця зовнішня міра, як легко переконатися, володіє властивістю для кожної множини із .

Повертаючись до загального випадку, розглянемо довільну зовнішню міру . Оскільки для довільних множин та із виконується , то

, (1)

причому (1) перетворюється в рівність для кожної множини , такої, що .

Важливим є той випадок, коли (1) перетворюється в рівність, справедливу для фіксованої множини , і довільної множини .

Означення 2_. Множина , називається - вимірною (вимірною відносно зовнішньої міри ), якщо

. (2)

Зрозуміло, що умова (2) виконується для всіх множин таких, що . Отже, множина , є - вимірна тоді і лише тоді, коли (2) виконується для всіх множин , таких, що .

Позначимо сукупність усіх - вимірних підмножин множини через , і розглянемо функцію , яка є звуженням функції із на клас тобто таку функцію, що або інакше .

Теорема Каратеодорі. Якщо є довільна зовнішня міра, то сукупність усіх - вимірних множин є -алгебра множин із одиницею , а функція , яка є звуженням функції із на клас , є міра.

Оскільки , то . Якщо , то множина також належить . Справді, , внаслідок - вимірності множина . Очевидно, . Це тому, що і множина є -вимірна.

Покажемо, що є алгебра множин. Нехай та - довільні множини із класу . Тоді при довільній множині , справедливі рівності (внаслідок вимірності ) (внаслідок вимірності  ) , (3)

(внаслідок вимірності G) (4)

Із (3) та (4) випливає, що при довільній множині виконується

Отже, . Окрім того і . Отже, є алгебра із одиницею .

Покажемо, що є -алгебра множин. Нехай - довільна послідовність множин із . Покажемо, що . Оскільки є алгебра множин, то можна вважати, що множини попарно не перетинаються. Тоді для довільної множини , виконується (внаслідок - вимірності ) = , (5)

де , . Із рівності (5) і - вимірності множини випливає, що при довільній множині , виконується . Методом математичної індукції показуємо, що

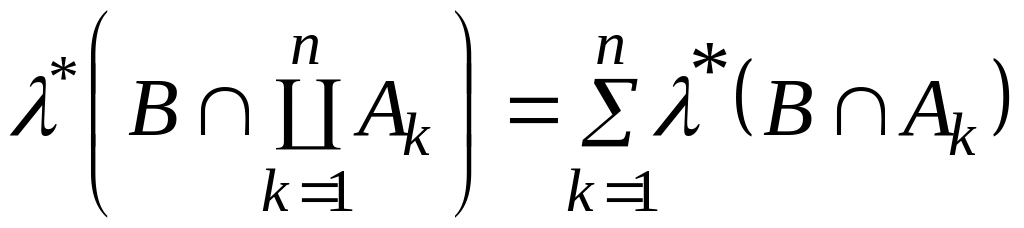(6)

при довільному і довільній множині .

Враховуючи - вимірність множини , рівність (6) та монотонність зовнішньої міри, дістанемо, що для довільної множини , виконується .

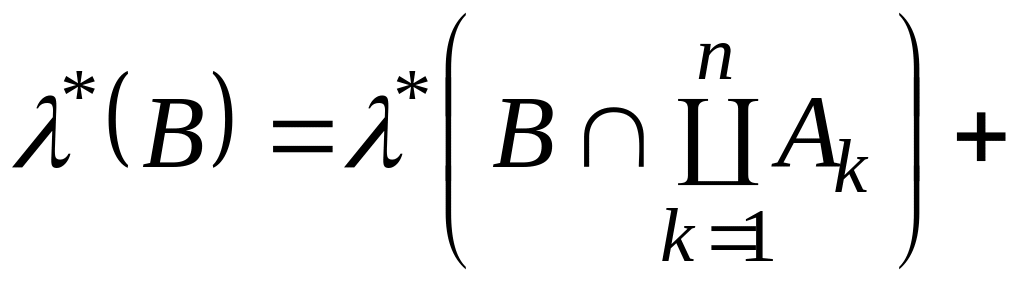
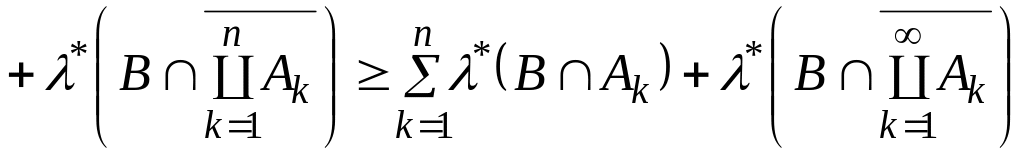Переходячи тут до границі при , дістанемо

. (7)

Оскільки і , то дістанемо . Оскільки , то . Отже, для довільної множини , справедливе .

Тому і, отже, є -алгебра множин.

Покажемо -аддитивність функції . Якщо в (7) покласти , де , то дістанемо .

Оскільки справедлива і протилежна нерівність, то .

Отже, є міра на -алгебрі . Теорему доведено.

Зауважимо, що міра , про яку іде мова в доведеній теоремі, називається мірою, породженою зовнішньою мірою .

Ця міра і -алгебра володіють властивостями:

1. ;

2. ;

3. 

;

4. .

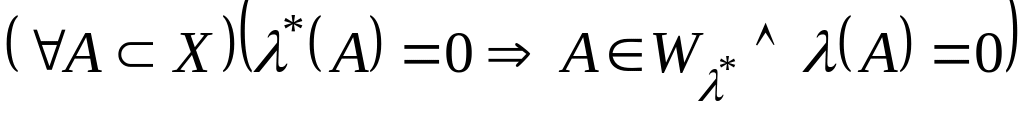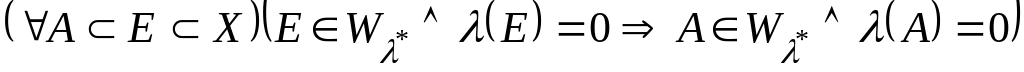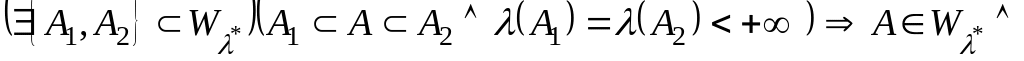
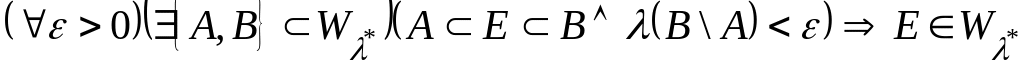Зауважимо, що останнє твердження вказує достатню умову - вимірності множини . Можна показати, що

.

Означення 3. Міра , що визначена на півкільці , називається повною, якщо .

Із твердження 2) випливає, що міра , яка породжена довільною зовнішньою мірою є повна міра на -алгебрі .