М. Є. Коренков, І. П. Головенко

Теорія міри і інтеграла

(курс лекцій)

Луцьк – 2008

УДК 517.51(07)

ББК 22.161я73

Рекомендовано до друку вченою радою Волинського державного університету імені Лесі Українки (протокол №1 від 25 вересня 2003 року).

Рецензенти:

Середа В. Ю., професор кафедри вищої математики Луцького технічного університету, канд. фіз.-мат. наук.

Філозоф Л. І., завідувач кафедри математичного аналізу ВНУ імені Лесі Українки, канд. фіз.-мат. наук.

  Коренков М. Є., Головенко І. П.

К66  Теорія міри і інтеграла (курс лекцій). – Луцьк: Волинська обласна друкарня, 2008. – 60 с.

Розглянуто основні класи множин та елементи загальної теорії міри і інтеграла.

УДК 517.51(07)

ББК 22.161я73

Передмова

Теорія міри і інтеграла Лебега була розроблена на початку ХХст. в зв'язку з потребами аналізу та теорії функцій. Абстрактний варіант цієї теорії тепер є математичною основою ряду теоретичних і прикладних розділів сучасної математики (теорія ймовірностей, функціональний аналіз, теорія оптимізації, математичні методи економіки і т. і.).

Цей посібник присвячений загальній теорії міри і інтеграла. Як часткові її випадки розглянуто тут міру Лебега і Жордана в просторі а також міру Лебега-Стілтьєса на прямій. Розглянуто тут також теорію вимірних функцій та різні види збіжності послідовності функцій, теорію інтеграла Лебега і питання про граничний перехід під знаком інтеграла Лебега, з'ясовано зв'язок між лебеговим та рімановим інтегралами.

Автори вдячні студентам математичного факультету ВНУ імені Лесі Українки Демчук В. Л., Горбач С. І., Стельмащук Л. В., Пугач Т. В., Грицюк І. А., за якісну підготовку курсу лекцій до опублікування.

Розділ і. Міра.

§1.1 Множини метричного простору.

Нагадаємо тут деякі поняття і факти, які будуть використовуватися пізніше. Через будемо позначати відповідно множину натуральних чисел, кільце цілих чисел, поля раціональних, дійсних та комплексних чисел.

Якщо - деяка непорожня множина, то через позначимо сукупність всіх підмножин цієї множини, . Очевидно, . Відомо, що різниця , де і - довільні множини, , називається доповненням множини (до множини ) і позначається або тобто .

Для довільної сукупності множин таких, що при , де - скінченна або нескінченна множина індексів , справедливі рівності

, ,

які називаються законами двоїстості або законами де Моргана.

Множини називаються диз’юнктивними, якщо . Обєднання таких множин позначається .

Відомо, що дві функції і називаються рівними (співпадаючими), якщо і .

Якщо , то функція така, що , називається звуженням функції на множину і позначається . При цьому функція називається продовженням (поширенням) функції із множини на множину .

Нагадаємо, що множина , , називається замкнутою в метричному просторі з метрикою , якщо вона містить всі свої граничні точки. Множина , , називається відкритою в метричному просторі , якщо кожна точка множини є внутрішньою точкою для неї, тобто належить разом зі всіма точками деякого свого околу. Відомо, що множина , , є відкрита (замкнута) в метричному просторі тоді і лише тоді, коли множина замкнута (відкрита) в .

Очевидно відкрита та замкнута, , , , кулі метричного простору є відповідно відкрита та замкнута множини в .

Справедливі наступні твердження:

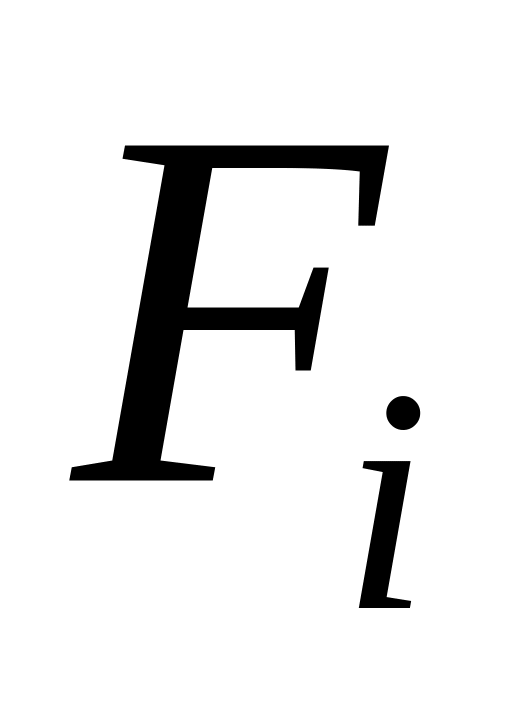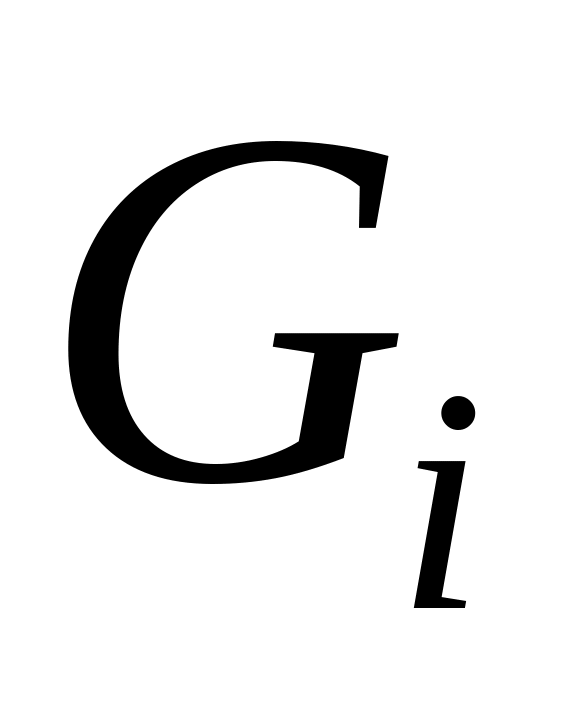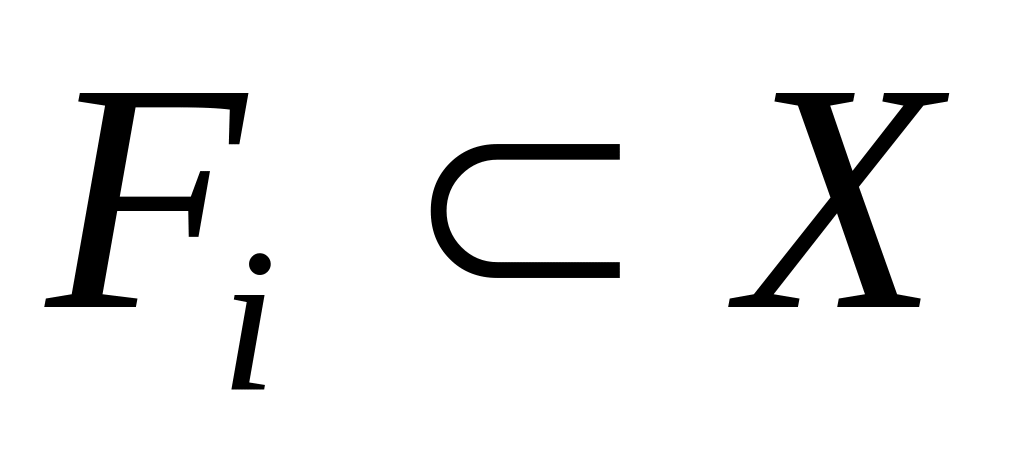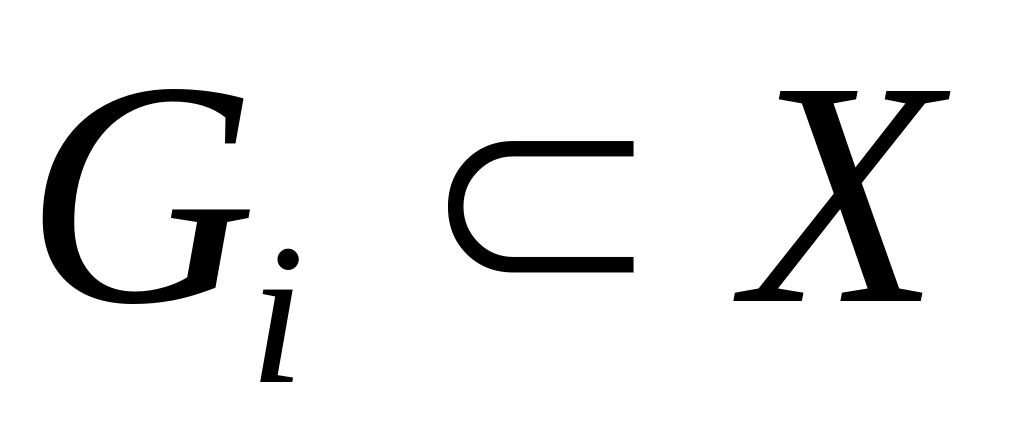
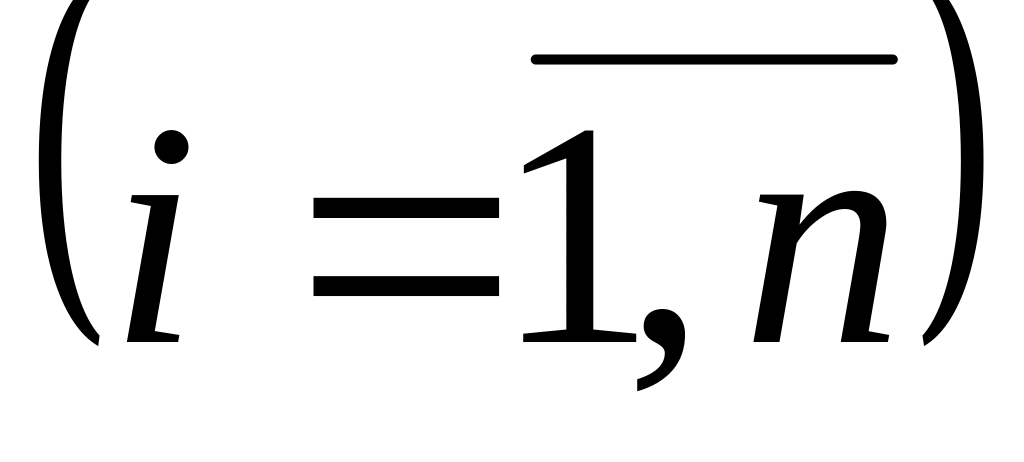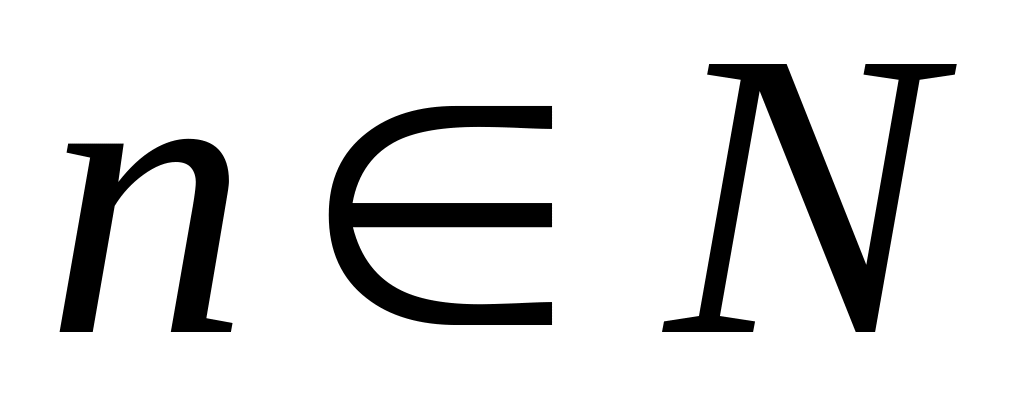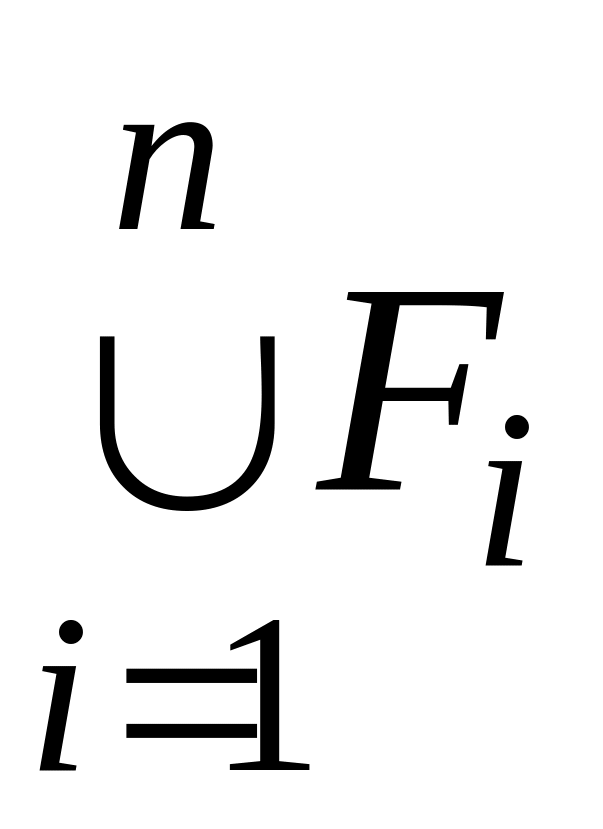1. якщо – замкнуті множини і - відкриті множини метричного простору , , , то при довільному , , множина замкнута, а множина 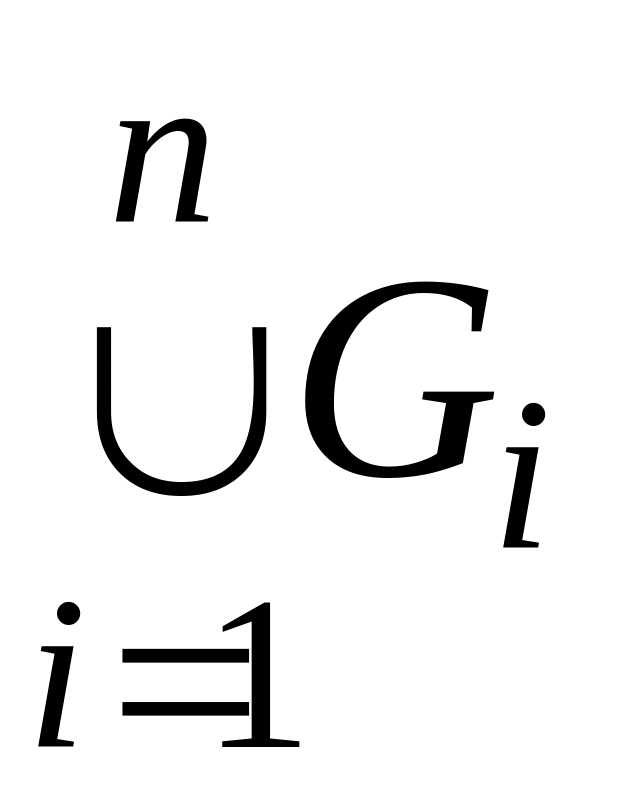відкрита в .

2. якщо - довільна скінченна або нескінченна множина індексів і множини 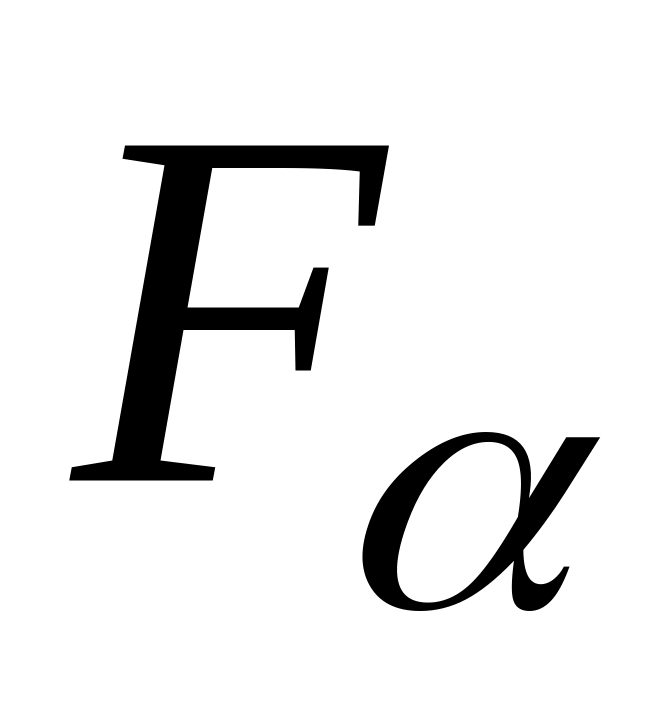, 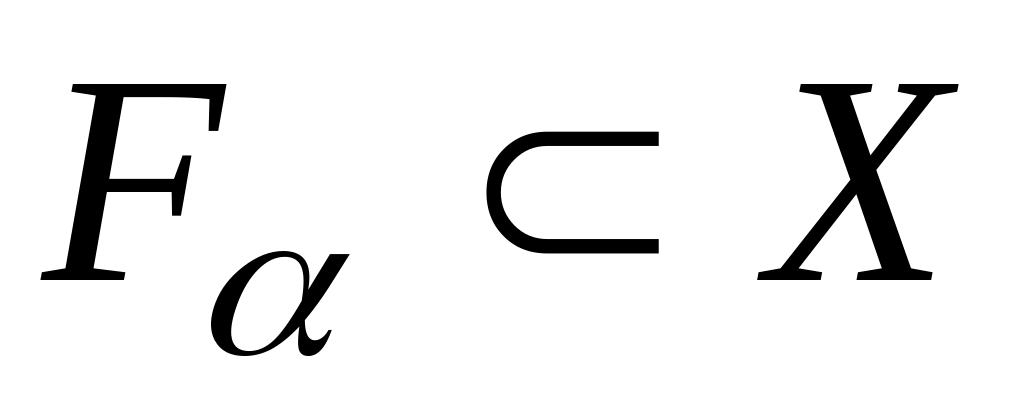при , та 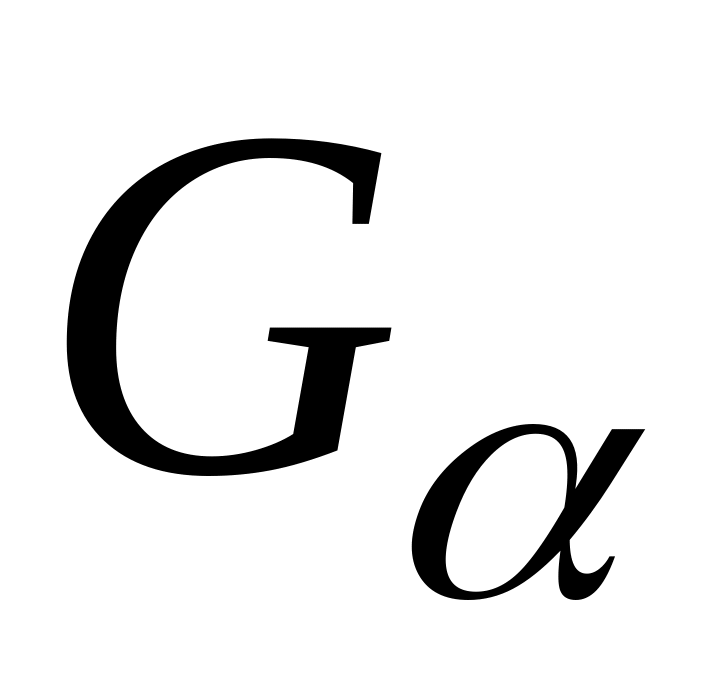, 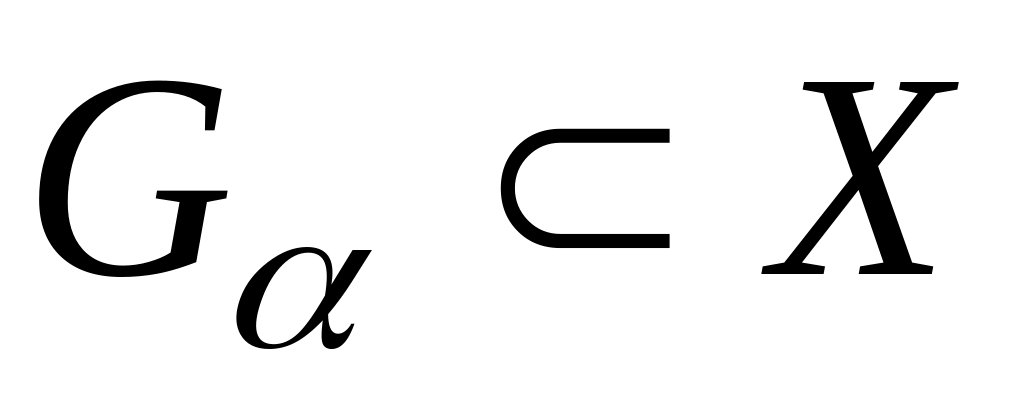при , відповідно замкнуті та відкриті в метричному просторі , то множини 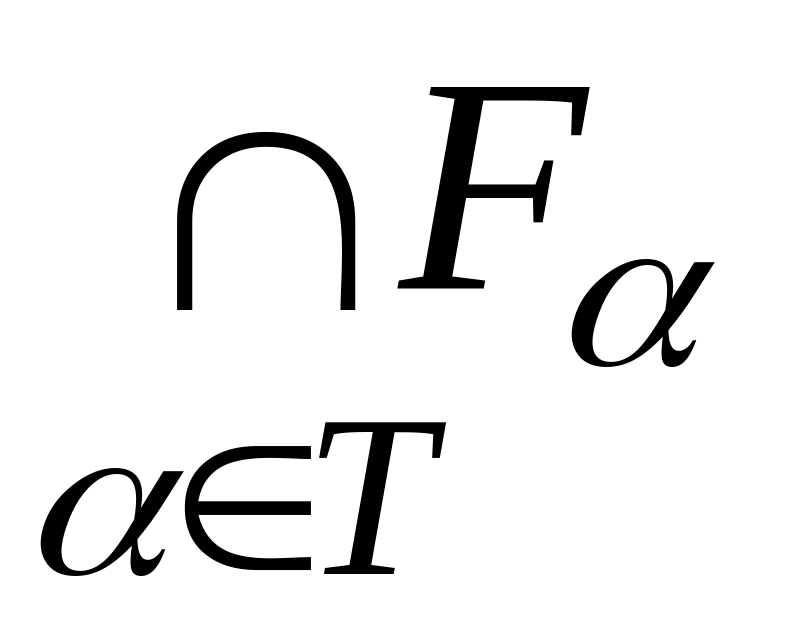, 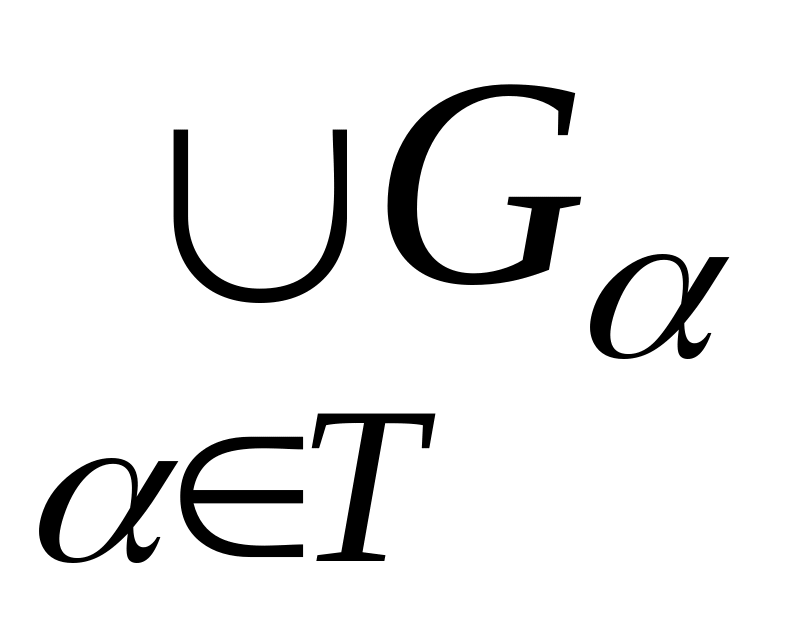є відповідно замкнута та відкрита в .

Можна показати, що кожна непорожня відкрита множина метричного простору , (тобто відкрита множина на числовій прямій) є або вся множина або обєднання не більш ніж зчисленної сукупності інтервалів (обмежених або необмежених), які попарно не перетинаються і кінці яких не належать (вони називаються складовими інтервалами множини ).

Кожна замкнута множина метричного простору є або вся множина або утворюється шляхом вилучення із не більш ніж зчисленної сукупності інтервалів, які попарно не перетинаються і кінці яких належать , якщо ці кінці не є символи та (такі інтервали називаються суміжними інтервалами для ).

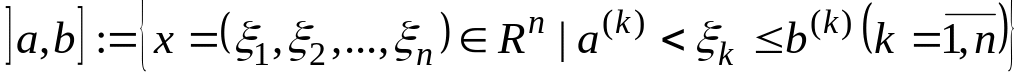Якщо , - дві фіксовані точки із , такі, що , то множина називається півінтервалом в або піввідкритим паралелепіпедом в .

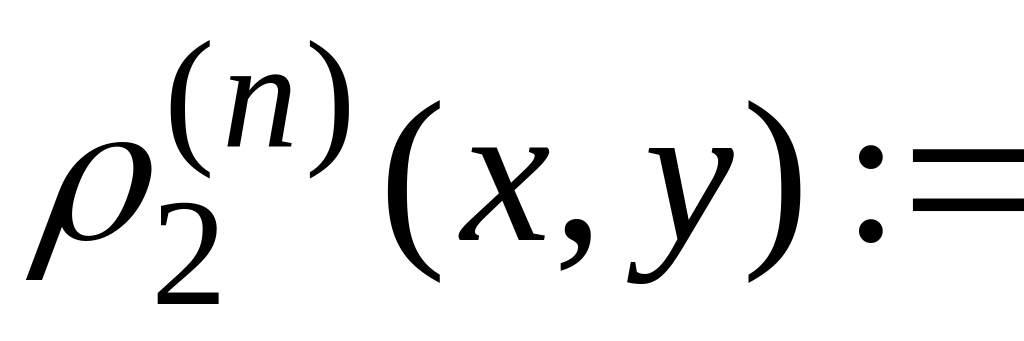
Можна показати, що кожна непорожня відкрита множина із метричного простору , де , , , є або вся множина або обєднання зчисленної сукупності півінтервалів із , які попарно не перетинаються. Вказане обєднання не може складатися зі скінченної сукупності півінтервалів.

З іншого боку, як можна показати, кожна непорожня відкрита множина із є або вся множина або обєднання не більш ніж зчисленної сукупності відкритих куль простору .