
- •Векторы. Линейные операции над векторами.
- •Скалярное произведение векторов и его свойства. Модуль вектора.
- •Линейная зависимость векторов.
- •Базис и ранг системы векторов.
- •Разложение вектора по базису.
- •Матрицы: основные понятия.
- •Линейные операции над матрицами и их свойства.
- •Транспонирование матриц. Умножение матриц.
- •Обратная матрица. Нахождение обратной матрицы с помощью присоединенной матрицы
- •Применение определителей. Формулы Крамера.
- •Системы линейных уравнений: основные понятия.
- •Методы решения систем линейных уравнений.
- •Совместность систем линейных уравнений. Теорема Кронекера-Капелли.
- •Однородные системы линейных уравнений.
- •Неоднородные системы. Структура общего решения системы линейных неоднородных уравнений.
- •Понятие линейного оператора.
- •Действия с линейными операторами.
- •Собственные векторы и собственные значения линейного оператора.
- •Линейная модель обмена.
- •Множества: основные понятия.
- •Операции над множествами и их свойства.
- •26. Понятие функции. Основные свойства функции.
- •Основные элементарные функции.
- •Последовательность. Предел последовательности.
- •Предел функции. Основные теоремы о пределах.
- •Два замечательных предела.
- •Второй замечательный предел:
- •31. Непрерывность функции: основные понятия.
- •32. Производная. Дифференцируемость функции.
- •33. Производные основных элементарных функций
- •34. Экстремум функции.
- •35. Выпуклость и вогнутость графика функции. Точки перегиба.
Векторы. Линейные операции над векторами.
Любой упорядоченный набор действительных чисел (а1, а2, …, аn) называется n-мерным вектором
 ,
=(а1,
а2,
…, аn)
,
=(а1,
а2,
…, аn)Линейные операции
Сумма двух n-мерных векторов =(а1, а2, …, аn) и
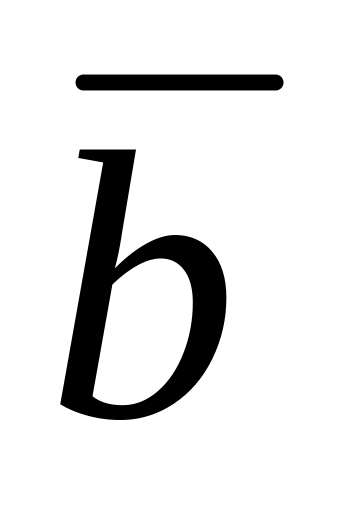 =(b1,
b2,
…, bn)
=(b1,
b2,
…, bn)
+ = (а1+ b1, а2+ b2, …, аn+ bn)
Разность векторов
- = +(- )
Произведение вектора на число k, k
 R
R
k =(kа1, kа2, …, kаn)
Скалярное произведение векторов и его свойства. Модуль вектора.
=(а1, а2, …, аn) и =(b1, b2, …, bn)
( , )=а1b1 + а2b2 + … + аnbn
Свойства скалярного произведения
( , )=( , )
(k , )=k( , )
( , +
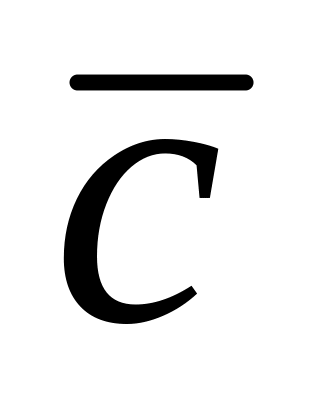 )=
(
,
)+(
,
)
)=
(
,
)+(
,
)( , )
 0,
причем (
,
)=0
тогда и только тогда, когда
– нулевой вектор
0,
причем (
,
)=0
тогда и только тогда, когда
– нулевой вектор
Линейная зависимость векторов.
Вектор называется линейной комбинацией векторов а1, а2, …, аs из Rn, если
 1a1+
1a1+ 2a2+…+
sas,
где
1,
2,…,
s
R.
В этом
случае говорят, что
линейно выражается через векторы
1,
2,
s
2a2+…+
sas,
где
1,
2,…,
s
R.
В этом
случае говорят, что
линейно выражается через векторы
1,
2,
s
Система векторов 1, 2,…, m называется линейно зависимой, если существуют такие числа 1, 2, m, не равные одновременно нулю, что
1a1+
2a2
+…+
mam=![]() (1)
(1)
В противном случае векторы называются линейно независимыми
Иначе говоря, векторы 1, 2,…, m линейно независимы, если из равенства (1) следует 1= 2=…= m=0
Базис и ранг системы векторов.
Система векторов называется базисом пространства Rn называется базисом, если:
эта система линейно независима
всякий вектор пространства Rn линейно выражается через векторы данной системы
Всякий вектор =(а1, а2, …, аn) представим в виде:
=
1![]() 1
+
2
2
+…+
n
n,
1
+
2
2
+…+
n
n,
то есть является линейной комбинацией векторов 1, 2,…, n
Теорема. Линейно независимая система векторов пространства Rn является базисом тогда и только тогда, когда число векторов равно n
Система векторов может иметь несколько базисов,
количество векторов в базисах должно быть одинаково;
число векторов базиса – ранг системы
Разложение вектора по базису.
Пусть система векторов
1=(а11, а12, …, а1n)
2=(а21, а22, …, а2n)
m=(аm1, аm2, …, аmn)
Является базисом
и вектор
![]() разложен по этому базису
разложен по этому базису
=х1 1 + х2 2 +…+ хm m
Теорема. Разложение вектора по векторам базиса единственно
Матрицы: основные понятия.
Матрица – произвольная система элементов совокупности К, расположенная в виде прямоугольной таблицы, содержащая m строк и n столбцов, называется (m, n) – матрицей или просто матрицей над множеством K
Общий вид (m, n) – матрицы
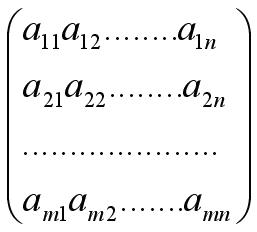
Матрицу, имеющую одну строку, называют просто строкой, а число её элементов – длиной строки
Матрицу, состоящую из 1 столбца, называют просто столбцом.
