Экзаменационный билет № 1

1. Эконометрика — это наука, которая дает количественное выражение взаимосвязей экономических явлений и процессов на базе. В качестве цели эконометрического моделирования обычно рассматривают анализ исследуемого экономического объекта ( процесса); прогноз его экономических показателей, имитацию развития объекта при различных значениях экзогенных переменных. Метод широко применим не только в эконометрическом моделировании, но и вообще в статистическом исследовании. Задачей курса Эконометрика является изучение наиболее распространенных методов эконометрического моделирования, реализация этих методов на практике и интерпретация полученных результатов. Применение эконометрики в анализе и прогнозировании социально-экономических явлений и процессов способствует выработке современного экономического мышления.

2. Общее назначение множественной регрессии состоит в анализе связи между несколькими независимыми переменными (называемыми также регрессорами или предикторами) и зависимой переменной. Суть регрессионного анализа: построение математической модели и определение ее статистической надежности.Вид множественной линейной модели регрессионного анализа:

Y = b₀ + b₁x_i1 + ... + b_jx_ij + ... + b_kx_ik + e_i . Основная задача регрессионного анализа заключается в нахождении по выборке объемом n оценки неизвестных коэффициентов регрессии.

Коэффициент детерминации- это доля дисперсии зависимой переменной, объясняемая рассматриваемой моделью зависимости, то есть объясняющими переменными. Более точно — это единица минус доля необъяснённой дисперсии . Определяется следующим образом:

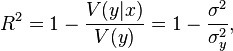
Коэффициент Фишера применяется для проверки равенства дисперсий двух выборок. Его относят к критериям рассеяния. В регрессионном анализе критерий Фишера позволяет оценивать значимость линейных регрессионных моделей. В частности, он используется вшаговой регрессии для проверки целесообразности включения или исключения независимых переменных .Формула вычисления критерия Фи­шера такова:

Экзаменационный билет № 2

1. Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности. Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. При однонаправленном соотношении малые значения одной переменной соответствуют малым значениям другой переменной, большие значения — большим. Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. 

R(xy)=

2. Нелинейная регрессия по включенным переменным не таит каких-либо сложностей в оценке ее параметров. Она определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), ибо эти функции линейны по параметрам. Так, в параболе второй степени

у= а0 + а1 х + а2 х2 + ε

Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например

– полиномы различных степеней – 

– равносторонняя гипербола –