Екзаменаційний білет № 13
Алгебра множин. Комп’ютерне подання множин.
§ 2. Комп’ютерне подання множин.
У комп’ютері можна подавати множини різними способами. Один зі способів — зберігати невпорядковані елементи множини. Проте в такому разі операції з множинами займатимуть багато часу через те, що потрібно щоразу переглядати елементи. Тому розглянемо інші способи.
Одним із найпоширеніших і найпростіших способів — подання множин за допомогою бітових рядків. Упорядкуємо довільним способом елементи універсальної множини. Нехай універсальна множина U містить п елементів, тоді U = {а1, а2,…, аn–1, аn}.
Множину A U подають у комп’ютері рядком із 0 і 1 довжиною п так: якщо аі є А, то і-й біт дорівнює 1, а ні, то 0.
Приклад
2.
Нехай U
=
{a,
b,
с,
d,
е,f,
т,
п,
р,
q},
А
=
{b,
т,
n,
q},
В
= {а,
b,
f,
т,
q}.
Тоді
множину А
подають рядком 0100001101, а множину В
—
рядком 1100011001. Тепер на комп’ютері легко
виконати операції над множинами А
та В.
Замінивши
Т на 1, а F на 0 у таблицях істиності для
логічних операцій
,
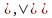та
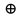(альтернативне «чи»), отримаємо таблиці
відповідних операцій над бітами. Будемо
також використовувати нотацію OR,
AND
і
ХOR
відповідно для логічних операцій
,
та
,
як у багатьох мовах програмування.
Значення операцій OR,
AND
і
ХOR
над бітами наведено в таблиці:
Неважко переконатись, що об’єднанню множин відповідає порозрядне OR над бітовими рядками, які подають множини А та В, а перетину множин — порозрядне AND над відповідними бітовими рядками.
-
Х
У
OR
AND
ХOR
0
0
0
0
0
0
1
1
0
1
1
0
1
0
1
1
1
1
1
0
Приклад 3.
Використаємо бітові рядки, які подають множини А та В з прикладу 2. Бітовий рядок, який відповідає об’єднанню цих множин А В = {a, b, f, m, п, q}, знаходимо як результат виконання операції порозрядного OR:
0100001101
1100011001
1100011101.
Бітовий рядок, який відповідає перетину множин А В = {b, т, q}, знаходимо як результат виконання операції порозрядного AND:
0100001101
1100011001
0100001001.
Якщо універсальна множина U має велику потужність, а її підмножини не дуже потужні, то подання за допомогою бітових рядків неефективне щодо витрат пам’яті. У такому разі доцільно використовувати інші структури даних — зазвичай зв’язані списки та хеш-таблиці. У певних задачах потрібні спеціальні методи подання множин, які ґрунтуються на використанні дерев.
Екзаменаційний білет № 14
Поняття відношення, задання відношень, основні властивості.
§ 1. Поняття відношення. Задання відношень.
Відношення - одне з основних понять сучасної математики. Мову відношень використовують для опису зв’язків між об’єктами та поняттями. Зокрема, поняття бінарного відношення дає змогу формалізувати операції попарного порівняння, і тому його широко використовують у теорії вибору, а реляційні бази даних ґрунтуються на концепції n-арних відношень. Найпростіший спосіб задати зв’язок між елементами двох множин — записати впорядковані пари елементів, що перебувають у цьому зв’язку. Нехай А та В — множини. Бінарне відношення з А в В — це якась підмножина R декартового добутку А В цих множин: R A B.
Визначення 6.1
Бінарне відношення з А в В — це множина впорядкованих пар, у якій перший елемент пари належить множині А, а другий — множині В.
Використовують
запис aRb,
якщо
(а,
b
)
R,
і
запис a
b,
якщо (a,
b)
R.
Бінарні відношення описують зв’язки між елементами двох множин. Зв’язки між елементами більше ніж двох множин задають n -арними відношеннями. Розглядаючи в певному контексті лише бінарні відношення, уживають термін „відношення” замість „бінарне відношення”.
Приклад 6.1. Нехай А = {0,1, 2}, В = {а, b} та задано відношення R = {(0, а), (0, b), (1, а), (2, b)}. Отже, ORa, бо (0, а) R, але 1 b, оскільки (1, b) R.
Здебільшого розглядають бінарні відношення за умови А = В. Відношенням на множині А називають бінарне відношення з А в А. Інакше кажучи, відношення R на множині А – цс підмножина декартового квадрату множини А, тобто R A2.
Приклад 6.2. Нехай А = {1, 2, 3, 4}. Які впорядковані пари утворюють відношення R = {(а, b) | а ділить b }? Очевидно, що R ={(1, 1), (1, 2), (1, 3), (1,4), (2, 2), (2, 4), (З, 3), (4,4)}.
Бінарне відношення можна задати за допомогою списку, елементами якого є пари, з яких складається відношення.
Приклад 6.3. На множинах чисел А = {1, 2, 3, 4, 5, 6, 7, 8, 9}; В = {24, 25, 26} побудуємо відношення «дільник», яке складається з упорядкованих пар виду (х,у), де х – дільник у, х А, у В. Позначимо це відношення через R:
R = {(1, 24), (1, 25), (1, 26), (2, 24), (2, 26), (3, 24), (4, 24), (5, 25), (6, 24), (8, 24)}
Бінарне відношення R на множинах Х і У можна задати за допомогою матриці, рядки якої відповідають елементам множини Х, стовпці – елементам множини У.
Приклад 6.3. Наступна матриця задає відношення R «дільник» для числових множин А та В з попереднього прикладу.
-
А В
24
25
26
1
1
1
1
2
1
0
1
3
1
0
0
4
1
0
0
5
0
1
0
6
1
0
0
7
0
0
0
8
1
0
0
9
0
0
0
Бінарне відношення R на множинах Х і У можна задати графічно. На площині зобразимо точками хі і уі елементи множин Х і У. Якщо пара (хі, уі) належить відношенню R, з’єднаємо точки хі і уі лінією, яка спрямована від першого елемента пари до другого. Позначивши таким чином всі пари , що належать відношенню R, одержимо фігуру, яка називається графом відношення.
Рис.
6.1
1 1 1 1
0 1 0 1
0 0 1 0
0 0 0 1
Визначення 6.2
Спрямовані лінії, що з’єднують пари точок, називаються дугами, а точки, що зображають елементи множини, – вершинами графа.
Розглянемо деякі часткові випадки відношень. Нехай задане бінарне відношення R на множині А: R А2. Можливий випадок, коли R = А2, – таке відношення називається повним. Може трапитися, що R = Ø, таке відношення називається порожнім. Якщо відношення містить всі можливі пари виду (а, а) і не містить інших пар елементів, відношення називається тотожнім.
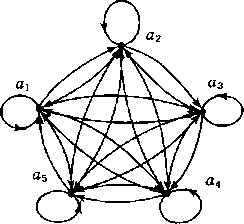Всі
елементи матриці повного відношення –
одиниці, порожнього відношення – нулі.
Рис. 1 Граф повного відношення