К зачету по сопромату 1 Вопрос Основные понятия и гипотезы сопротивления материалов Сопротивление материалов базируется на понятии «прочность», что является способностью материала противостоять приложенным нагрузкам и воздействиям без разрушения. Сопротивление материалов оперирует такими понятиями как: внутренние усилия, напряжения, деформации. Приложенная внешняя нагрузка к некоторому телу порождает внутренние усилия в нём, противодействующие активному действию внешней нагрузки. Внутренние усилия, распределенные по сечениям тела, называются напряжениями. Таким образом, внешняя нагрузка порождает внутреннюю реакцию материала, характеризующуюся напряжениями, которые в свою очередь прямо пропорциональны деформациям тела. Деформации бывают линейными (удлинение, укорочение, сдвиг) и угловыми (поворот сечений). Основные понятия сопротивления материалов, оценивающие способность материала сопротивляться внешним воздействиям:
Прочность — способность материала воспринимать внешнюю нагрузку не разрушаясь;
Жесткость — способность материала сохранять свои геометрические параметры в допустимых пределах при внешних воздействиях
Устойчивость — способность материала сохранять в стабильности свою форму и положение при внешних воздействиях
Расчет реальных конструкций и их элементов является либо теоретически невозможным, либо практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов применяется модель идеализированного деформируемого тела, включающая следующие допущения и упрощения:
Гипотеза сплошности и однородности: материал представляет собой однородную сплошную среду; свойства материала во всех точках тела одинаковы и не зависят от размеров тела.
Гипотеза об изотропности материала: физико-механические свойства материала одинаковы по всем направлениям.
Гипотеза об идеальной упругости материала: тело способно восстанавливать свою первоначальную форму и размеры после устранения причин, вызвавших его деформацию.
Гипотеза (допущение) о малости деформаций: деформации в точках тела считаются настолько малыми, что не оказывают существенного влияния на взаимное расположение нагрузок, приложенных к телу.
Допущение о справедливости закона Гука: перемещения точек конструкции в упругой стадии работы материала прямо пропорциональны силам, вызывающим эти перемещения.
Принцип независимости действия сил (принцип суперпозиции): результат воздействия нескольких внешних факторов равен сумме результатов воздействия каждого из них, прикладываемого в отдельности, и не зависит от последовательностиих приложения.
Гипотеза Бернулли о плоских сечениях: поперечные сечения, плоские и нормальные к оси стержня до приложения к нему нагрузки, остаются плоскими и нормальными к его оси после деформации.
Принцип Сен-Венанна: в делениях, достаточно удалённых от мест приложения нагрузки, деформация тела не зависит от конкретного способа нагружения и определяется только статическим эквивалентом нагрузки.
Эти положения ограниченно применимы к решению конкретных задач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда
2 вопрос Метод сечений для определения внутренних сил в брусе Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.
Разрежем стержень,
находящийся в равновесии под действием
некоторой системы сил 
на две части плоскостью, перпендикулярной
к его оси z.
Отбросим одну из частей стержня и рассмотрим оставленную часть.
Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами
Вопрос 3 Дифференциальные и интегральные зависимости между интенсивностью распределенной нагрузки и внутренними силами
Дифференциальные зависимости между распределенной нагрузкой, поперечной силой и изгибающим моментом:
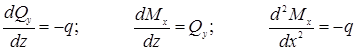
Дифференциальные
зависимости используются
для контроля правильности построенных эпюр
поперечных сил 
и
изгибающих моментов 
.
Помимо дифференциальных зависимостей существуют интегральные зависимости, получаемые из формул дифференциальных зависимостей. Например, изгибающий момент равен определенному интегралу по длине участка балки. Используя интегральную зависимость между изгибающим моментом и поперечной силой и аналитическое выражение поперечных сил, можно построить эпюру изгибающих моментов, не определяя выражение для них.
В формулах дифференциальных и интегральных зависимостей распределенная нагрузка (q) положительна, если направлена вниз.
Вопрос 4 Напряжения и деформации в деформируемом теле Деформа́ция (от лат. deformatio — «искажение») — изменение взаимного положения частиц тела, связанное с их перемещением относительно друг друга. Деформация представляет собой результат изменения межатомных расстояний и перегруппировки блоков атомов. Обычно деформация сопровождается изменением величин межатомных сил, мерой которого является упругое механическое напряжение.
Деформации разделяют на обратимые (упругие) и необратимые (пластические, ползучести). Упругие деформации исчезают после окончания действия приложенных сил, а необратимые — остаются. В основе упругих деформаций лежат обратимые смещения атомов металлов от положения равновесия (другими словами, атомы не выходят за пределы межатомных связей); в основе необратимых — необратимые перемещения атомов на значительные расстояния от исходных положений равновесия (то есть выход за рамки межатомных связей, после снятия нагрузки переориентация в новое равновесное положение).
Пластические деформации — это необратимые деформации, вызванные изменением напряжений. Деформации ползучести — это необратимые деформации, происходящие с течением времени. Способность веществ пластически деформироваться называется пластичностью. При пластической деформации металла одновременно с изменением формы меняется ряд свойств — в частности, при холодном деформировании повышается прочность.
Механическое напряжение — это мера внутренних сил, возникающих в деформируемом теле, под влиянием различных факторов. Механическое напряжение в точке тела определяется как отношение внутренней силы к единице площади в данной точке рассматриваемого сечения.
Напряжения являются результатом взаимодействия частиц тела при его нагружении. Внешние силы стремятся изменить взаимное расположение частиц, а возникающие при этом напряжения препятствуют смещению частиц, ограничивая его в большинстве случаев некоторой малой величиной.
Q — механическое напряжение.
F — сила, возникшая в теле при деформации.
S — площадь.
Различают две составляющие вектора механического напряжения:
Нормальное механическое напряжение — приложено на единичную площадку сечения, по нормали к сечению (обозначается
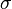).Касательное механическое напряжение — приложено на единичную площадку сечения, в плоскости сечения по касательной (обозначается
).
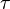Совокупность напряжений, действующих по различным площадкам, проведенным через данную точку, называется напряженным состоянием в точке.
В Международной системе единиц (СИ) механическое напряжение измеряется в паскалях.
Вопрос 5 Деформации, напряжения и потенциальная энергия при растяжении Растяжение-сжатие — в сопротивлении материалов — вид продольной деформации стержня или бруса, возникающий в том случае, если проходит через его центр масс.
Называется также одноосным или линейным напряжённым состоянием. Является одним из основных видов напряжённого состояния параллелепипеда. Может быть также двух- и трёх-осным[1]. Вызывается как силами, приложенными к концам стержня, так и силами, распределёнными по объёму (силы инерции и тяготения).
Растяжение вызывает удлинение стержня (также возможен разрыв и остаточная деформация), сжатие вызывает укорочение стержня (возможна потеря устойчивости и возникновение продольного изгиба).
В поперечных сечениях бруса возникает один внутренний силовой фактор — нормальная сила. Если растягивающая или сжимающая сила параллельна продольной оси бруса, но не проходит через неё, то стержень испытывает т. н. внецентренное растяжение (сжатие). В этом случае за счёт эксцентриситета приложения нагрузки в стержне кроме растягивающих (сжимающих) напряжений возникают ещё и изгибные напряжения.
Напряжение вдоль оси прямо пропорционально растягивающей или сжимающей силе и обратно пропорционально площади поперечного сечения. При упругой деформации между напряжением и относительной деформацией определяется законом Гука, при этом поперечные относительные деформации выводятся из продольных путём умножения их на коэффициент Пуассона. Пластическая деформация, предшествующая разрушению части материала, описывается нелинейными законами.
Согласно закону сохранения энергии, работа внешних сил не исчезает, а переходит в потенциальную энергию (V), накапливаемую в упругом теле при его деформировании.
Следовательно, потенциальная энергия деформации численно равна работе внешних сил при нагружении тела (или работе внутренних сил, совершаемой ими в процессе разгружения).
Таким образом, потенциальная энергия деформации стержня, испытывающего, например, растяжение, кручение и прямой поперечный изгиб, равна:
.
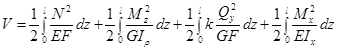Как видно из этой формулы, потенциальная энергия деформации всегда положительна, поскольку она является квадратичной функцией обобщенных сил (или обобщенных перемещений, так как последние линейно связаны с обобщенными силами). Отсюда следует, что потенциальная энергия, накопленная в результате действия группы сил, не равна сумме потенциальных энергий, накопленных от действия каждой нагрузки в отдельности. То есть принцип независимости действия сил при вычислении потенциальной энергии деформации не применим.