3.1. Нагрузки и усилия в балке

Вычисляем погонную равномерно распределенную нагрузку на балку:

q_n =1,02 (g_n +S_n)·B;

q=1,02 (g+S)·B

q_nl = 1,02 (3,88 + 0,9)6 = 29,25 кН/м;

q = 1,02 (4,45 +1,8)6 = 49,02 кН/м.

Расчетный пролет балки: l₀ = 12 – 0,2 = 11,8 м.

Вычисляем максимальные усилия в балке:

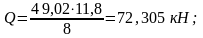
3.2. Предварительный подбор поперечного сечения балки

Определяем требуемый момент сопротивления поперечного сечения стальной балки:

где с₁=1,1.

Вычисляем предельные значения высоты составной балки:

где k = 1,25 для балки постоянного сечения;

Учитывая, что высота балки должна быть в пределах h_min< h < h_opt, а также то, что высота стенки балки h_w должна быть согласована с сортаментом (см. табл. 14 или 15 приложения 2), принимаем h_w = 85 см. Тогда высота балки примерно составит h=85/0,95=89,5 см.

Определяем толщину стенки балки:

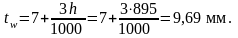
Принимаем по сортаменту толщину стенки балки t_w=10 мм = 1 см.

Определяем размеры горизонтальных полок балки.

Вычисляем момент инерции двух полок:

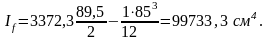
Тогда площадь одной полки составит:

Назначаем ширин полки b_f =25см, тогда её толщина составит:

T_f =A_f/b_f = 24,9/25 = 0,9 см.

Примем в соответствии с сортаментом t_f = 22 мм.

3.3. Проверка скомпонованного сечения по первой и второй группам предельных состояний

Вычисляем фактические и геометрические состояния балки:

h = 85 + 2·2,2 = 89,4 см;

A=h_wt_w + 2b_f t_f.

A =85·1+ 2·2,2·25 = 195 см²;

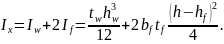
I_x = 1·85³/12 + 2·25·2,2[(89,4 – 2,2)/2] ² = 260282,7см⁴;

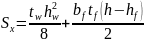
S_x = 25·2,2(89,4 – 2,2)/2+1·85²/8 = 3301,1 см³;

W_x = 2·260282.7/89,4 = 5822,9 см³.

Проверяем нормальные и касательные напряжения:

σ_max =

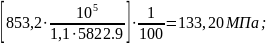
σ_max < R_y = 230 МПа;

τ_max = [72,305·10³·3301,1/(260282,7·1)] ·1/100 = 91,7 МПа;

τ_max< R_s = 91,7 МПа.

3.3.1. Проверяем жесткость балки

Вычислим прогиб балки от постоянной и длительной нагрузок:

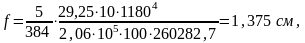
что меньше предельного прогиба балки (см. табл. 11 приложения 2):

f_u= l / 250 = 1180/250 = 4,72 см.

Следовательно, прочность и жесткость балки отвечают требованиям Норм.

Проверяем запас прочности балки:

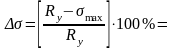[(230–133,20)/230]·100% = 0,8%, что меньше 5%.

3.3.2. Проверяем местную устойчивость элементов балки

Местная устойчивость сжатого пояса будет обеспечена при соблюдении условия:

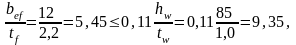
где = (25 – 1)/2 = 12,0 см.

Условие соблюдается.

Устойчивость стенки балки при наличии местного напряжения от опирания плит перекрытия будет обеспечена при соблюдении условия:

Это большое предельно допустимого значения 2,5. Следовательно, стенка балки должна быть укреплена парными поперечными ребрами жесткости.

Ширина ребра должна быть не менее

(850/30) + 40 = 68,3 мм,

принимаем b_h = 80 мм; с треугольными вырезами в местах сварки стенки и потолок, размером с=60 мм, d = 40 мм.

Толщина ребер принимается не менее

В соответствии с сортаментом принимаем толщину ребра 6 мм. Поперечные ребра приваривают к стенке сплошными двухсторонними швами толщиной k_f = 5 мм.

Расстояние между ребрами не должно превышать 2h_w = 2·85 = 170 см.

Ребра ставим на расстоянии, равном ширине плиты покрытия b = 1,5 м, поэтому проверять верхний пояс балки на местную нагрузку нет необходимости.

Устойчивость стенки при действии нормальных напряжений будет обеспечена, если соблюдается условие:

Это меньше t_w = 1,0 см. Следовательно, условие удовлетворяется.