Задачи к курсу «Эконометрика».

§ 1. Корреляционный анализ. Сведения из теории.

Двумерная модель.

1. Оценки:

2. Проверка значимости

.

Здесь – уровень значимости, – объем выборки, -квантиль распределения Стьюдента с n степенями свободы. Коэффициент детерминации указывает долю дисперсии одной случайной величины, обусловленную вариацией другой.

3. Преобразование Фишера

.

Доверительный интервал с доверительной вероятностью , -квантиль уровня нормальной случайной величины

u , где .

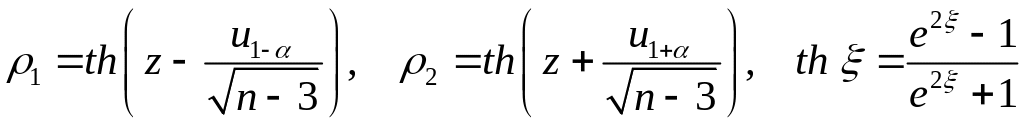4. Доверительные интервалы для коэффициентов регрессии

где .

5. Вычисление корреляционного отношения (коэффициента корреляции)

,

где , =DY, D(Y| )-условная дисперсия случайной величины Yпри условии, что .

Трехмерная модель:

Пусть имеется 3 фактора .

– вектор среднеквадратичных отклонений.

– матрица парных коэффициентов корреляции.

1. Точечные оценки частных коэффициентов корреляции

где – алгебраические дополнения к элементу матрицы ,

– определитель матрицы .

2. Проверка значимости частных коэффициентов корреляции

.

3. Преобразование Фишера

.

Доверительный интервал с доверительной вероятностью ,

где .

4. Проверка значимости множественных коэффициентов корреляции

.

Здесь - квантиль распределения Фишера с степенями свободы. Справедливость альтернативной гипотезы означает, что имеет место линейная статистическая зависимость между фактором и факторами и .

Задачи по корреляционному анализу.

Двумерная модель .

Задача 1. Пусть имеется выборка объема и вычисленное значение эмпирического коэффициента корреляции . Найти доверительный интервал для неизвестного коэффициента корреляции на уровне значимости и проверить значимость коэффициентов корреляции при .

Решение:

1. Проверим гипотезу о значимости коэффициента корреляции

Значит, значимо отличен от нуля.

2. Найдем доверительный интервал для с доверительной вероятностью .

.

Если , то . Тогда ,

,

Значит, .

Задача 2. Пусть имеется выборка объема и вычисленное значение эмпирического коэффициента корреляции . Найти доверительный интервал для неизвестного коэффициента корреляции на уровне значимости и проверить значимость коэффициентов корреляции при .

Задача 3. Какое наименьшее значение коэффициента корреляции следует считать значимым на уровне значимости, если объем выборки .

Задача 4. На основе годового отчета 100 предприятий об оплате труда (руб. за 1 чел. час) и затратах труда (кол-во чел. час за ед. продукции) провести корреляционный анализ, если

Решение

1. Проверим значимость коэффициента корреляции. Здесь

.

Значит, коэффициент корреляции значимо отличается от нуля. Статистическую связь между случайными величинами и можно считать доказанной.

2. Найдем с надежностью интервальную оценку для коэффициента корреляции .

,

с вероятностью .

.

3. Найдем точечные оценки коэффициентов регрессии:

Точечные оценки уравнений регрессии имеют вид:

4. Найдем интервальные оценки коэффициентов регрессии

Выводы:

1. Доказана значимость связи между оплатой труда за 1 ч. и затратах труда на единицу продукции. Связь является отрицательной, то есть увеличение одного из показателей соответствует уменьшению среднего значения другого показателя.

2. При этом увеличение оплаты труда на 1 руб. за человеко-час соответствует уменьшение затрат на чел.-час на 1 продукции в среднем. С вероятностью можно утверждать, что указанная величина принадлежит .

3. Так как с вероятностью , то можно сказать, что изменение одного из показателей соответствует изменению другого на величину (от до ). Отставшая до величина соответствует изменению неконтролируемых (случайных) показателей.

Задача 5. По результатам выборки объема из двумерной нормальной генеральной совокупности получены выборочные характеристики

Проверить значимость коэффициентов корреляции, найти доверительный интервал для .

Задача 6. Из двумерной нормальной генеральной совокупности взята выборка объема и найдены выборочные коэффициенты регрессии , . Проверить значимость коэффициента корреляции при и найти доверительный интервал.

Задача 7. На основе 16 выборочных данных получены следующие характеристики: где .

Требуется при проверить значимость коэффициента корреляции.

Задача 8. Пусть , где случайные ошибки имеют следующие характеристики: , и статистически независимы,

Доказать, что , то есть теснота линейной корреляции связи между случайными величинами ослабевает при аддитивном наложении на них случайных ошибок.

Задача 9. По данным 100 выборочных наблюдений об объеме реализованной продукции и себестоимости единицы продукции было выяснено, что при увеличении объема на единицу его измерения себестоимость уменьшается в среднем на единиц своего измерения. А при увеличении себестоимости на единицу объем реализованной продукции уменьшается в среднем на единиц. С надежностью найти:

интервальную оценку генерального коэффициента корреляции между и .

интервальную оценку коэффициентов регрессии себестоимости единицы продукции от объема реализации.

Задача 10. На основании 20 наблюдений было выяснено, что выборочная доля дисперсии случайной величины , вызванная вариацией , составляет . Найти интервальную оценку коэффициентов корреляции с надежностью , если связь между и положительна.

Задача 11. В таблице приведены данные о месячных темпах роста потребительских цен (инфляции) полученных за 10 месяцев 1992 г. ( ) и 10 месяцев 1993 г. ( ) начиная с марта.

месяцы	март	апрель	май	июнь	июль	август	сентябрь	октябрь	ноябрь	декабрь
	1.3	1.22	1.12	1.19	1.11	1.1	1.12	1.23	1.26	1.25
	1.18	1.19	1.18	1.2	1.22	1.26	1.23	1.2	1.16	1.13

Требуется найти:

оценку коэффициента корреляции между и и при проверить его значимость;

оценку коэффициента регрессии ;

оценку уравнения регрессии зависимости от ;

при найти интервальные оценки для и .

Трехмерная модель.

Задача 1. По результатам наблюдений найдены выборочные характеристики трехмерной нормальной генеральной совокупности

проверить значимость частных коэффициентов корреляции при ; множественного коэффициента корреляции при .

найти доверительный интервал для с надежностью .

Решение

1. Найдем точечную оценку

.

2. Проверим значимость частного коэффициента корреляции

, справедлива альтернативная гипотеза.

3. Найдем интервальные оценки для с доверительной вероятностью .

.

4. 

.

Справедлива .

Задача 2. При исследовании взаимосвязи следующих макроэкономических показателей 10 различных стран мира за 1992 г.

– ВНП,

– промышленное производство,

– индекс цен,

– доля безработных

получены следующие данные:

.

Для требуется:

проверить значимость частного коэффициента корреляции при и найти интервальные оценки с .

при проверить значимость множественного коэффициента корреляции .

Задача 3. По данным задачи 2

вычислить и сравнить с соответствующими парными коэффициентами корреляции.

при проверить значимость , а также найти его интервальную оценку с надежностью .

при проверить значимость множественного коэффициента корреляции .

Задача 4. По результатам наблюдений найдены выборочные характеристики трехмерной генеральной совокупности:

Требуется:

проверить значимость частных коэффициентов корреляции при ; множественного коэффициента корреляции при .

найти интервальную оценку для с надежностью .