6.3. Одноканальная смо с отказами

Рассмотрим СМО с одним каналом обслуживания, в которую поступает поток требований с интенсивностью λ. Интенсивность обслуживания одного требования равна μ. Требуется найти предельные вероятности состояний системы и показатели ее эффективности. Система S в данном случае имеет 2 состояния: S₀ — канал свободен и S₁ канал занят. Нарисуем граф состояний системы, т.е. геометрическую схему, на которой состояние системы изображаются прямоугольниками, а переходы из состояния в состояние — стрелками:

λ

S₀ μ S₁

p₀ p₁

Для составление уравнения предельных состояний применяется правило: слева в уравнениях стоит предельная вероятность данного состояния р_i, умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в состояние I, на вероятности тех состояний, из которых эти потоки выходят.

Для данного графа система уравнений для вероятностей состояний имеет вид:

 ρ₀=μ ρ₁

 ρ₁=λ ρ₀

т.е. имеет одинаковые уравнения. Учитывая, что р₁+р₀=1, получаем систему:

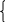
 ρ₀=μ ρ₁

ρ₁=ρ₀ =1 (6.6)

Обозначим:

 =λ/μ (6.7)

Величина  называется интенсивностью загрузки канала. Она выражает среднее число требований, приходящее за среднее время обслуживания, одного требования. Тогда из системы (6.6), с учетом формулы (6.7), получим выражения для предельных вероятностей состояний:

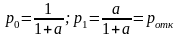(6.8)

р₀ — вероятность того, что канал обслуживания свободен, т.е. характеризует относительную пропускную способность СМО.

р₁ — вероятность того, что канал занят, т.е. вероятность отказа.

Абсолютная пропускная способность:

A= λ  p₀ (6.9)

Среднее число занятых обслуживанием каналов:

N=   (1– P_отк) (6.10)

Пример: Стол заказов магазина принимает заказы по одному телефону. Заявки поступают с интенсивностью 80 заявок в час, а среднее время оформления одной заявки 3 минуты. Определить показатели эффективности работы стола заказов.

Решение: λ=80заявок/час, =3мин.

Вычислим интенсивность загрузки канала . При этом следует обратить внгимание, что при вычислении , λ и  должны иметь одинаковую временную размерность. Поэтому в нашем примере нужно преобразовать одну из данных величин, например, .

=2мин=3/60часа=1/20часа.

Тогда

1. Доля времени простоя канала:

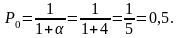
Следовательно, 20% времени канал будет свободен, значит в среднем только 20% заявок может быть обслужено.

2. Доля заявок, получивших отказ в обслуживании, равна:

т.е. 80% времени телефон будет занят обслуживанием.

3. Абсолютная пропускная способность системы:

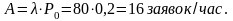
Из вычислений видно, что СМО с одним телефоном будет плохо справляться с потоком заявок, т.к. потери поступающих заявок составляют 80%, а вероятность обслуживания всего 20%. Кроме того, низка абсолютная пропускная способность системы – только 16 завявок из 80 поступивших.