
- •С одержание
- •Глава 1. Моделирование систем. Системный подход. Системный анализ 6
- •Глава 2. Модели сетевого планирования и управления 21
- •Глава 3. Балансовые модели 42
- •Глава 4. Задачи линейного программирования 52
- •Введение
- •Глава 1. Моделирование систем. Системный подход. Системный анализ
- •1.1. Основные понятия. Методы исследования систем
- •1.2. Экономические системы, методы их исследования и моделирования
- •1.3. Основные понятия и этапы экономико-математического моделирования систем
- •1.4. Классификация экономико-математических методов и моделей
- •Глава 2. Модели сетевого планирования и управления
- •2.1. Назначение и области применения сетевого планирования и управления
- •2.2. Сетевая модель и ее основные элементы
- •2.3. Порядок и правила построения сетевых графиков
- •2.4. Упорядочивание сетевого графика
- •2.5. Понятие о пути
- •2.6. Временные параметры сетевых графиков
- •2.7. Анализ и оптимизация сетевого графика
- •2.8. Анализ и оптимизация календарных сетей
- •2.9. Оптимизация сетевого графика с целью сокращения длины критического пути
- •Глава 3. Балансовые модели
- •3.1. Понятие о межотраслевом балансе
- •3.2. Межотраслевая балансовая модель и ее свойства
- •3.3. Задачи, решаемые с помощью балансовой модели
- •3.4. Решение системы балансовых уравнений в матричной форме
- •3.5. Экономический смысл элементов матрицы, коэффициентов полных косвенных внутрипроизводственных затрат, прямых и полных затрат труда и капиталовложений
- •Глава 4. Задачи линейного программирования
- •4.1 Модели линейного программирования
- •4.2 Графический метод решения задач линейного программирования
- •4.3 Каноническая форма задач линейного программирования
- •4.4 Понятие о симплекс-методе
- •4.5 Двойственность в линейном программировании
- •4.6 Транспортная задача
- •Глава 5. Элементы теории игр
- •5.1. Понятие об игровых моделях
- •5.2. Платежная матрица
- •5.3. Нижняя и верхняя цена игры
- •5.4. Решение игры в смешанных стратегиях
- •5.5. Методы решения простейших игровых задач
- •5.6. Приведение матричной игры к задаче линейного программирования
- •5.7 Моделирование экономических ситуаций в терминах "Игры с природой"
- •Глава 6. Моделирование систем массового обслуживания
- •6.1. Основные понятия. Классификация смо
- •6.2. Основные компоненты смо
- •6.3. Одноканальная смо с отказами
- •6.4 Многоканальная смо с отказами
- •6.5. Одноканальная смо с очередью
- •6.6. Многоканальная смо с очередью
- •6.7. Имитационное моделирование смо
- •Глава 7. Модели управления запасами
- •7.1. Основные понятия
- •7.2. Экономико-математичесчкая постановка задачи управления товарными запасами на складе торговой фирмы для одной группы товаров
- •Глава 8. Понятие о статистическом моделировании
- •8.1. Примеры моделирования случайных процессов методом Монте-Карло
- •8.2. Определение характеристик стационарного случайного процесса
- •8.3. Оценка точности характеристик. Необходимое число реализаций
- •9. Особенности применения экономико-математических моделей в железнодорожном транспорте
- •9.1. Экономико-математическое моделирование реформирования
- •Структурных подразделений железнодорожного транспорта
- •9.2 Мировой опыт анализа реформирования структурных подразделений железнодорожного транспорта
- •Литература
4.5 Двойственность в линейном программировании
Понятие о двойственных задачах линейного программирования. Каждой задаче линейного программирования, которую назовем исходной, можно поставить в соответствие некоторую другую задачу линейного программирования, называемую двойственной к ней. Вместе взятые, эти задачи образуют пару взаимно двойственных задач и любую из них можно рассматривать как исходную. Решая одну из этих задач, можно получить решение и другой задачи.
Двойственная задача — это вспомогательная задача линейного программирования, получаемая с помощью определенных правил непосредственно из условий исходной. Сформулируем правила построения двойственных задач:
Если целевая функция f исходной задачи максимизируется, то целевая функция z двойственной — минимизируется, и наоборот.
Количество ограничений (m) исходной задачи равно количеству переменных двойственной, а количество переменных (n) исходной равно количеству ограничений двойственной. Переменные двойственной задачи обозначим через
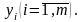 .
.Поскольку переменные исходной задачи связаны с ограничениями двойственной, каждой переменной
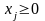 соответствует в двойственной задаче
ограничение вида
соответствует в двойственной задаче
ограничение вида
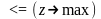 или
или
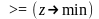 ,
и наоборот.
,
и наоборот.Каждой переменной
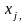 неограниченной
по знаку, соответствует ограничение
вида «=» двойственной задачи, и наоборот.
неограниченной
по знаку, соответствует ограничение
вида «=» двойственной задачи, и наоборот.Свободные члены ограниченной исходной задачи
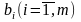 в
двойственной являются коэффициентами
при переменных
в
двойственной являются коэффициентами
при переменных
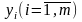 в целевой функции, а коэффициенты
в целевой функции, а коэффициенты
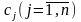 при переменных
при переменных
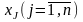 в целевой функции исходной задачи
являются свободными членами ограничений
двойственной.
в целевой функции исходной задачи
являются свободными членами ограничений
двойственной.Матрица А коэффициентов при неизвестных в ограничениях исходной задачи в двойственной транспонируется
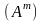 .
.
Для наглядности связь между исходной и двойственной задачами представлена в таблице 16.
Таблица 16
Исходная задача |
Двойственная задача |
Максимизация f Количество ограничений m Переменные
xj ³0 i-е ограничение вида «£» хj не ограничено по знаку i-е ограничение вида «=» Свободные члены ограничений bi Коэффициенты при xj в целевой функции (cj) Матрица коэффициентов при неизвестных в ограничениях (А) |
Минимизация z Количество ограничений n Переменные
j-е ограничение вида «³» yi ³0 j-е ограничение вида «=»
Коэффициенты при yi в целевой функции (bi) Свободные члены ограничений (cj) Транспонированная матрица коэффициентов при неизвестных в ограничениях (AT) |
Рассмотрим в общем виде одну из частных задач линейного программирования, которую будем считать исходной:
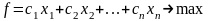
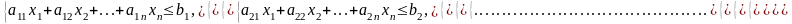
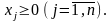
Двойственная к этой задаче будет иметь вид:
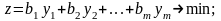
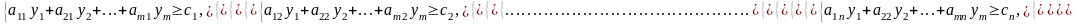
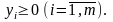
Если применить правила построения двойственных задач, то получим исходную задачу.
В таблице 17 приведены
частные виды исходных задач линейного
программирования в матричном виде и
соответствующие им двойственные задачи.
Через
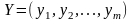 обозначена матрица — строка неизвестных
двойственной задачи.
обозначена матрица — строка неизвестных
двойственной задачи.
Матрица-строка Y умножается слева на матрицу — столбец В (в целевой функции) и матрицу А (в ограничениях), исходя из правил умножения двух матриц, а также правил построения двойственных задач (в частности, в двойственной задаче матрица коэффициентов при неизвестных в ограничениях должна быть транспонированной).
Первые две пары взаимно двойственных задач в таблице 17 называются симметричными, вторые две — несимметричными из-за наличия ограничений вида «=».
Используя правила построения двойственных задач и таблицу 11, для любой задачи линейного программирования можно построить двойственную к ней.
Таблица 17
|
Исходная задача |
Двойственная задача |
|
I |
f=CX®max AX≤B X≥0 |
z=YB→min YA≥C Y≥0 |
Симметричные задачи |
II |
f=CX→min AX≥B X≥0 |
z=YB→max YA≤C Y≥0 |
|
III |
f=CX®max AX=B X≥0 |
z=YB→min YA≥C |
Несимметричные задачи |
IV |
f=CX→min AX=B X≥0 |
z=YB→max YA≤C |
Пример: Построить задачу, двойственную к данной:
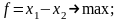
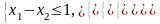
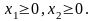
Чтобы построить двойственную задачу, исходную необходимо привести к форме (I) путем умножения обеих частей второго ограничения на (–1). После этого преобразования исходная задача примет вид:
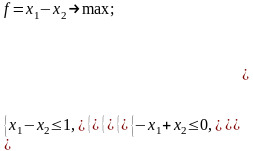
Двойственная задача:
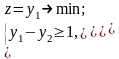
Пример: Построить задачу, двойственную к данной:
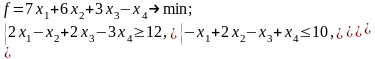
Для построения двойственной задачи воспользуемся формами (II), (IV) и преобразуем данную задачу путем умножения обеих частей второго неравенства на (–1). Тогда исходная задача будет иметь вид:
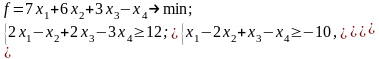
Двойственная задача:
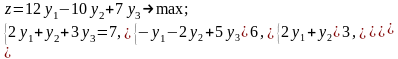
Используя пример,
поясним некоторые правила построения
двойственных задач. Поскольку количество
ограничений исходной задачи m=3,
двойственная задача должна иметь три
переменные:
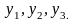 Количество переменных исходной задачи
n=4, поэтому двойственная должна
иметь четыре ограничения. Переменные
x1 и x4
исходной задачи не ограничены по
знаку. В силу этого первое и четвертое
ограничения двойственной задачи имеют
вид равенств. Третье ограничение исходной
задачи имеет вид равенства, следовательно,
переменная y3 двойственной
задачи не ограничена по знаку.
Количество переменных исходной задачи
n=4, поэтому двойственная должна
иметь четыре ограничения. Переменные
x1 и x4
исходной задачи не ограничены по
знаку. В силу этого первое и четвертое
ограничения двойственной задачи имеют
вид равенств. Третье ограничение исходной
задачи имеет вид равенства, следовательно,
переменная y3 двойственной
задачи не ограничена по знаку.
Контрольные вопросы и упражнения
Что представляет собой двойственная задача линейного программирования?
В чем отличие симметричных задач двойственной пары от несимметричных?
Постройте задачи, двойственные к данным:

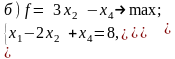
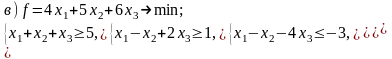
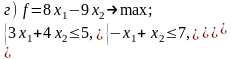
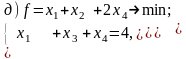

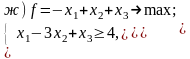
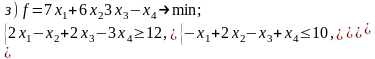
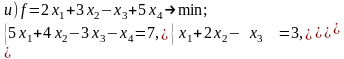
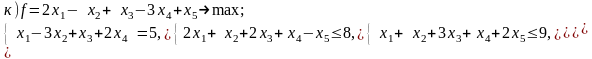
Дайте экономическую интерпретацию задачи, двойственной к задаче использования ресурсов.
Какая задача из пары взаимно двойственных задач может быть принята в качестве исходной и какая в качестве двойственной? Какие задачи на практике считают двойственными?
С какими вариантами решений можно столкнуться при исследовании задач двойственной пары?
Доказано, что при существовании допустимых планов у исходной и двойственной задач исходная задача имеет оптимальный план. Докажите существование оптимального плана у двойственной задачи при тех же условиях.
Постройте задачу, двойственную к данной:
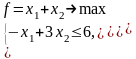
Решите исходную и двойственную задачи графическим методом.
9. Постройте задачи, двойственные к данным:
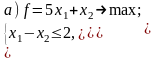
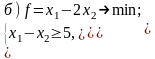
Решите исходную и двойственную задачи графическим методом. Проанализируйте результаты решения для каждой пары задач.
10. Как по решению исходной задачи найти решение двойственной и наоборот?

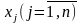
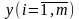
 не ограничено
по знаку
не ограничено
по знаку