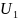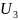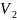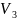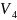- •Транспортная задача.
- •Решение.
- •80 Единиц товара.
- •90 Единиц товара, оставшиеся на втором складе.
- •150 Единиц товара, оставшиеся на втором складе.
- •Первое приближение получено.
- •Второе приближение
- •Второе приближение.
- •Третье приближение.
- •Четвертое приближение.
- •Пятое приближение.
- •Анализ итогового плана.
Первое приближение получено.
Мы имеем 6 занятых ячеек и 6 пустых.
Обратите внимание - сумма чисел по строкам совпадает с элементами
матрицы А, а сумма чисел по столбцам с элементами матрицы В.
Теперь добавим в нашу таблицу значения матрицы С. Эти числа мы будем
располагать в ячейках с левой стороны.
|
120 |
90 |
150 |
70 |
80 |
2 80 |
6 |
2 |
0 |
170 |
6 40 |
1 90 |
5 40 |
0 |
180 |
1 |
4 |
4 110 |
0 70 |
Посчитаем стоимость перевозок, заданных планом первого приближения.
Берем количество товара в занятых ячейках и умножаем на стоимость
перевозки, получаем:
F=80*2+40*6+90*1+40*5+110*4+70*0 = 1130
Это стоимость всех перевозок при использовании плана первого
приближения
Метод потенциалов.
Для уменьшения расходов на перевозки (оптимизации плана перевозок)
будем использовать метод потенциалов.
Следуем двум правилам:
1) Сумма потенциалов для занятых клеток должна быть равна
стоимости перевозки.
Например, для ячейки (3,2)
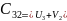
2) Нужно найти такой план перевозок при котором сумма потенциалов
в пустых ячейках будет не больше цены.
Потенциалы u расположим справа от таблицы, а потенциалы v под
таблицей. Суммы потенциалов будем вписывать в левой части ячеек.
В результате сформирован первый план перевозок, который является допустимым, так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план соответствует системе ограничений транспортной задачи.
2. Подсчитаем число занятых клеток таблицы, их 6, а должно быть m + n - 1 = 6. Следовательно, таблица невырожденным.
Затраты : F(x) = 2*80 + 6*40 + 1*90 + 5*40 + 4*110 + 0*70 = 1130
Потенциалы u расположим справа от таблицы, а потенциалы v под таблицей. Суммы потенциалов будем вписывать в левой части ячеек.
|
120 |
90 |
150 |
70 |
|
80 |
2 80 |
6 |
2 |
0 |
|
170 |
6 40 |
1 90 |
5 40 |
0 |
|
180 |
1 |
4 |
4 110 |
0 70 |
|
|
|
|
|
|
|
Потенциалов всего 7, а занятых ячеек (следовательно и уравнений) 6
Значит можно одному из потенциалов дать произвольное значение
Пусть u1= 0.
|
120 |
90 |
150 |
70 |
|
80 |
2 80 |
6 |
2 |
0 |
= 0 |
170 |
6 40 |
1 90 |
5 40 |
0 |
|
180 |
1 |
4 |
4 110 |
0 70 |
|
|
|
|
|
|
|
Находим в первой строке (там где у нас
u1) занятую ячейку. Это
ячейка (1,1). Применяем для нее правило
1.
 =
=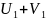 ;
2=0+
;
;
=2
;
2=0+
;
;
=2
Заносим = 2 в таблицу.
|
120 |
90 |
150 |
70 |
|
80 |
2 80 2 |
6 |
2 |
0 |
= 0 |
170 |
6 40 |
1 90 |
5 40 |
0 |
|
180 |
1 |
4 |
4 110 |
0 70 |
|
|
= 2 |
|
|
|
|
В первой строке больше нет занятых ячеек. Занятая ячейка есть в первом столбце (для которого мы уже нашли ( = 2).
Это ячейка (2,1). Применяем для нее правило 1.
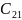 =
= ;
6 =
+
;
6 =
+ ;
=4
;
=4
Заносим = 4 в таблицу.
|
120 |
90 |
150 |
70 |
|
80 |
2 80 2 |
6 |
2 |
0 |
= 0 |
170 |
6 40 |
1 90 |
5 40 |
0 |
= 4 |
180 |
1 |
4 |
4 110 |
0 70 |
|
|
= 2 |
|
|
|
|
В первом столбце больше нет занятых ячеек. Занятая ячейка есть во второй строке (для которой мы уже нашли ( = 4).
Это ячейка (2,2). Применяем для нее правило 1.
 =
=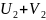 ;
1 = 4 +
;
= -3
;
1 = 4 +
;
= -3
Заносим = -3 в таблицу.
|
120 |
90 |
150 |
70 |
|
80 |
2 80 2 |
6 |
2 |
0 |
= 0 |
170 |
6 40 |
1 90 |
5 40 |
0 |
= 4 |
180 |
1 |
4 |
4 110 |
0 70 |
|
|
= 2 |
= -3 |
|
|
|
Аналогично находим ; ;
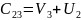 ;
5 = 4+
;
= 1
;
5 = 4+
;
= 1
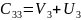 ;
4 = 1+
;
= 3
;
4 = 1+
;
= 3
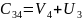 ;
0 =
+3;
= -3
;
0 =
+3;
= -3
Все потенциалы найдены. Заносим суммы потенциалов во все пустые
ячейки.
|
120 |
90 |
150 |
70 |
|
80 |
2 80 2 |
6 -3 |
2 1 |
0 0 |
= 0 |
170 |
6 40 6 |
1 90 1 |
5 40 5 |
0 0 |
= 4 |
180 |
1 5 |
4 0 |
4 110 4 |
0 70 0 |
= 3 |
|
= 2 |
= -3 |
=1 |
= -3 |
|
Теперь видим, что практически во всех ячейках сумма потенциалов не равны
цены. Значит план - неоптимальный.