Транспортная задача.

Задана матрица запасов товара на трех складах

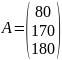
На первом складе а1=100 единиц товара, на втором складе а2=200 единиц

товара и на третьем складе а3=90 единиц товара.

Задана матрица потребностей магазинов в этом товаре

Для первого, второго и третьего магазина соответственно.

В тарифной матрице указаны стоимости перевозки единицы товара с конкретного склада в конкретный магазин. Например с31=1 означает, что стоимость (цена) перевозки единицы товара с третьего склада в первый магазин равна 1.

Нужно найти матрицу перевозок х32, например, в этой матрице означает количество товара перевозимого с третьего склада во второй магазин.

Матрица Х должна быть подобрана таким образом, чтобы:

1) Все магазины были обеспечены товаром;

2) Суммарная стоимость перевозок была минимальной.

Решение.

Если суммарные складские запасы равны суммарным потребностям

магазинов, то задача называется транспортной задачей закрытого типа.

В нашей задаче суммарные складские запасы равны

80+170+180 = 430

Суммарные потребности магазинов:

120+90+150 = 360

Запасы превышают потребности на 430-360=70 единиц. Мы имеем дело с

транспортной задачей открытого типа.

Перейдем к транспортной задаче закрытого типа, добавив четвертый (виртуальный) магазин с потребностью в 70 единиц товара.

Виртуальный магазин означает, что эти 70 единиц товара просто останутся

на каком-то складе и, следовательно затраты на их перевозку - нулевые.

Матрицы В, С и Х теперь примут вид:

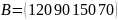
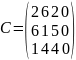
Если траспортная задача закрытого типа (изначально) то матрицы В,С и Х

изменять не надо.

При поиске решения мы будем использовать метод потенциалов и нам

понадобится еще одна матрица - матрица потенциалов:

Начинаем формировать план перевозок.

На первом этапе создадим первое приближение (первый вариант плана).

Затем, при помощи метода потенциалов улучшим этот план -

получим второе приближение. И так далее, пока не получим оптимальный

план с наименьшими расходами не перевозки.

Для удобства вычислений расположим матрицу А слева от матрицы Х,

а матрицу В - сверху.

Значения матрицы Х будем заносить в таблицу:

	120	90	150	70
80
170
180

Первое приближение найдем методом «северо-западного» угла. .

Начинаем с самой «северо-западной» ячейки - (1,1)

Эту, и последующие за ней ячейки, нужно максимально заполнить.

Первый склад может поставить 80 единиц товара, а первый магазин

может принять 120 единиц товара. Выбираем наименьшее из этих

значений - 80 и заносим в ячейку.

Больше 80 в эту ячейку мы не можем записать, т.к. на первом складе всего