§2. Уравнение неразрывности
Основным условием,
которое должно соблюдаться при течении
жидкости или газа, является непрерывность
изменения параметров потока в зависимости
от координат и времени, т.е. при течении
жидкости должны быть соблюдены условия
сплошности. Жидкость или газ должны
двигаться в соответствующих каналах
как сплошная среда без разрывов.
Сформулируем это условие. Отнесем поток
жидкости к системе координат
(рис. 7). В потоке выберем точку
с координатами
.
Изолируем неподвижный объем в форме
параллелепипеда со сторонами
Составляющие скорости течения жидкости
в точке
равны
.
Через площадку параллелепипеда
,
определяемую точкой
,
в течение времени
внутрь параллелепипеда втекает масса
жидкости, равная
.
Из объема параллелепипеда
в течение времени
через площадку
,
положение которой определяется точкой
с
координатами
вытекает масса жидкости, равная
Следовательно, при
течении жидкости с составляющей скорости
в точке
масса жидкости в объеме
изменяется на величину
При прохождении жидкости через другие грани параллелепипеда масса жидкости в объеме меняется аналогично:
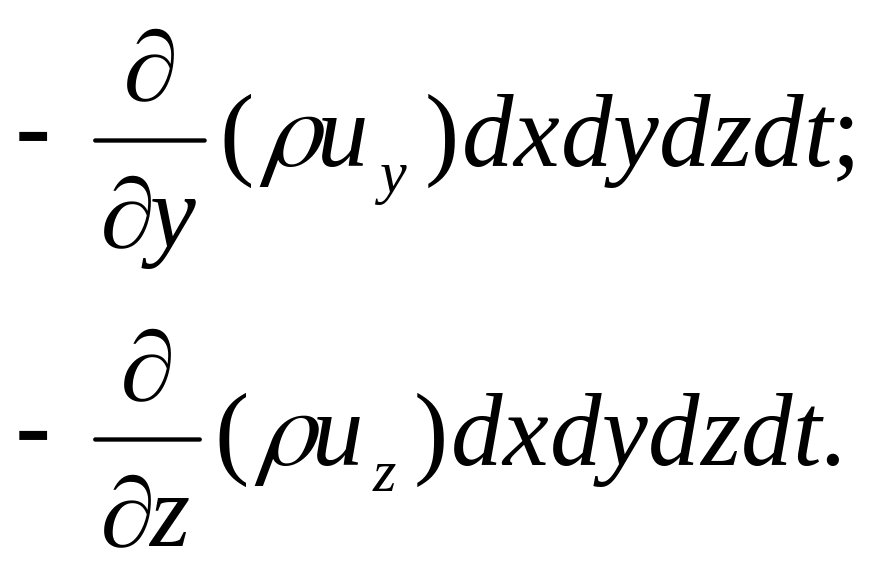
Суммарное изменение массы жидкости (газа) в фиксированном объеме равно:
.
Объем вполне определенный, и его величина не зависит от времени, координаты точки фиксированы.
Изменение массы
жидкости объеме
может произойти только за счет изменения
плотности
за период времени
.
В общем случае
В рассматриваемом случае
фиксированы и плотность может изменяться
только в зависимости от времени.
Плотность жидкости
в объеме, ограниченном
,
может изменяться на (
)
,
а масса жидкости в этом объеме за период
времени
на
.
Для сохранения сплошности жидкости должно быть удовлетворено условие:
.
Величина
входит в левую и правую части равенства,
поэтому условие соблюдения сплошности
потока в точке будет:
(8)
или
Уравнение (8) в гидромеханике называют уравнением неразрывности.
Если течение
установившееся, то
,
и условие сохранения сплошности течения
можно представить следующим образом:
(9)
т.е.
Когда жидкость, кроме того, еще и несжимаемая, то и тогда
(10
)
Рассмотрим теперь уравнение неразрывности для случая течения струйки при установившемся движении. Масса жидкости струйки течет в трубке тока (рис.8).
Пусть сечение 1-1
трубки тока имеет площадь
,
и в этом сечении скорость жидкости
,
а ее плотность
.
Площадь сечения 2-2 трубки тока равна
,
скорость -
и ее плотность
.
Скорости струйки касательны к стенкам
трубки тока, поэтому через стенки обмен
массой с окружающей жидкостью отсутствует.
Через сечение 1-1 в трубку тока в единицу
времени поступает масса жидкости, равная
.
Через сечение 2-2 вытекает в единицу
времени масса жидкости, равная
.
В трубке тока масса жидкости, находящаяся
между сечениями 1-1 и 2-2, остается
постоянной, следовательно, условие
сплошности потока в трубке тока будет:
,
т.е. вдоль трубки тока произведение
остается постоянным.