3. Конспект лекций по дисциплине

Лекция №1

Предмет механики жидкости и газа. Основные свойства жидкостей. Гипотеза сплошности. Сжимаемость, Вязкость.

Предметом механики жидкости и газа является модель сплошной текучей среды.

Под сплошной средой понимают непрерывное, безграничное или ограниченное множество материальных точек с непрерывным распределением по их множеству кинематических, динамических и других физических характеристик.

Основные законы, используемые в механике жидкостей и газов, - те же, что и в механике твердых тел. Однако применение этих законов к задачам МЖГ отличается некоторыми особенностями вследствие различия свойств жидкостей и твердых тел. Поэтому изучение МЖГ целесообразно начать с определения и оценки основных свойств жидкостей.

Жидкости отличаются от твердых тел легкой подвижностью частиц. Для изменения формы твердого тела к нему нужно приложить конечные, иногда очень большие силы. А изменение формы жидкости может происходить под действием даже самых малых сил (жидкость течет под действием собственного веса).

Жидкость, как и всякое физическое тело, имеет молекулярное строение, т.е. состоит из молекул, расстояние между которыми во много раз превосходит размеры самих молекул, т.е. жидкость, строго говоря, имеет прерывистую структуру. В МЖГ при решении большинства задач принимают жидкость как сплошную непрерывную среду ввиду чрезвычайной малости не только самих молекул, но и расстояний между ними. Тем самым, вместо самой жидкости изучается ее модель, обладающая свойством непрерывности. Гипотеза о непрерывности или сплошности жидкой среды упрощает исследование, так как позволяет рассматривать все механические характеристики жидкой среды: скорость, плотность, давление как функции координат точки в пространстве и времени.

Жидкости по своим механическим свойствам разделяются на два класса: малосжимаемые (капельные) и сжимаемые (газообразные). В дальнейшем, под жидкостью будем понимать всякую среду, обладающую свойством текучести.

Основные свойства жидкостей, существенные при рассмотрении задач МЖГ, - плотность и вязкость, а в некоторых случаях имеет значение также поверхностное натяжение жидкостей.

Плотность и удельный вес жидкостей. Плотностью жидкости называется ее масса , заключенная в единице объема :

. (1)

Если жидкость неоднородна, то формула (1) определяет лишь среднюю плотность жидкости. Для определения плотности в данной точке следует пользоваться формулой

. (2)

Вес жидкости , приходящийся на единицу объема , называется удельным весом:

. (3)

Если жидкость неоднородна, то для определения удельного веса жидкости в данной точке применяется формула

. (4)

Плотность и удельный вес связаны между собой соотношением

, (5)

где ускорение свободного падения.

Сжимаемость и температурное расширение жидкостей. Сжимаемость капельных жидкостей под действием давления характеризуется коэффициентом объемного сжатия , который представляет собой относительное изменение объема жидкости на единицу изменения давления:

, (6)

где первоначальный объем жидкости; изменение этого объема при увеличении давления на величину .

Коэффициент объемного сжатия имеет размерность Па^-1. Знак «минус» в формуле (6) обусловлен тем, что положительному приращению давления соответствует отрицательное приращение (т.е. уменьшение) объема жидкости .

Температурное расширение капельных жидкостей характеризуется коэффициентом температурного расширения , выражающим относительное увеличение объема жидкости при увеличении температуры на 1 град, т.е.

, (7)

где изменение этого объема при повышении температуры на величину .

В отличие от капельных жидкостей газы характеризуются значительной сжимаемостью и высокими значениями коэффициента температурного расширения.

Вязкость жидкостей. Вязкостью называется свойство жидкостей оказывать сопротивление сдвигу. Все реальные жидкости обладают определенной вязкостью, которая проявляется в виде внутреннего трения при относительном перемещении смежных частиц жидкости. Наряду с легкоподвижными жидкостями (водой, воздухом) существуют очень вязкие жидкости, сопротивление которых сдвигу весьма значительно (глицерин, тяжелые масла). Таким образом, вязкость характеризует степень текучести жидкости или подвижности ее частиц.

Пусть жидкость течет вдоль плоской стенки параллельными ей слоями (рис.1), как это наблюдается при ламинарном движении. Вследствие тормозящего влияния стенки слои жидкости будут двигаться с разными скоростями, значения которых возрастают по мере отдаления от стенки. Рассмотрим два слоя жидкости, движущиеся на расстоянии друг от друга. Слой движется со скоростью , а слой со скоростью . Вследствие разности скоростей слой сдвигается относительно слоя на величину (за единицу времени). Величина является абсолютным сдвигом слоя по слою , а есть градиент скорости (относительный сдвиг). Появляющееся при этом движении касательное напряжение (сила трения на единицу площади) обозначают буквой . Тогда аналогично явлению сдвига в твердых телах можно предположить зависимость между напряжением и деформацией в виде:

, (8)

или, если слои будут находиться бесконечно близко друг к другу,

. (9)

Напряжение всегда положительно, поэтому в формуле (9) следует ставить знак плюс или минус, в зависимости от знака . Величина , характеризующая сопротивляемость жидкости сдвигу, называется динамической или абсолютной вязкостью. Выражение (9) называют законом трения Ньютона.

Наряду с понятием абсолютной или динамической вязкости в МЖГ находит применение понятие кинематической вязкости , представляющей собой отношение динамической вязкости к ее плотности:

. (10)

Таблица 1. Плотность и удельный вес капельных жидкостей при С.

Жидкость	, Н/м2	, кг/м2
Вода пресная » морская Глицерин безводный Керосин Масло касторовое » минеральное Нефть Ртуть Спирт этиловый безводный Хлористый натрий (раствор) Эфир этиловый Бензин авиационный	9 790 10 010 – 10 090 12 260 7770 – 8450 9520 8000 – 8750 8340 – 9320 132 900 7440 10 690 7010 – 7050 7250 - 7370	998,2 1002 – 1029 1250 792 – 840 970 877 – 892 850 – 950 13 547 789,3 1200 715 – 719 739 - 751

Таблица 2. Приближенные значения плотности и удельного веса газов при давлении Па и =15 ⁰ С.

Газ	, Н/м2	, кг/м2
Водород Водяной пар Окись углерода Азот Воздух Кислород Углекислота	0,81 7,25 11,3 11,3 11,6 12,8 17,6	0,08 0,74 1,15 1,15 1,20 1,30 1,80

Таблица 3. Значения коэффициента объемного сжатия воды

Температура, С	Па-1, при давлении, Па
	50	100	200	390	780
0 5 10 15 20	5,4 5,29 5,23 5,18 5,15	5,37 5,23 5,18 5,1 5,05	5,31 5,18 5,08 5,03 4,95	5,23 5,08 4,98 4,88 4,81	5,15 4,93 4,81 4,7 4,6

Таблица 4. Коэффициент температурного расширения воды

Давление, Па	град. при температуре,
	1 - 10	10 - 20	40 - 50	60 - 70	90 - 100
10 980 1960 4900 8830	1,000014 0,000043 0,000072 0,000149 0,000229	0,000150 0,000165 0,000183 0,000236 0,000294	0,000422 0,000422 0,000426 0,000429 0,000437	0,000556 0,000548 0,000539 0,000523 0,000514	0,000719 0,000714 - 0,000661 0,000621

Лекция №2

Действительная и идеальная жидкость. Основные параметры течений.

Линии и трубки тока. Лагранжевый и Эйлеровый способ задания движения сплошной среды.

Простейшей схемой движущейся жидкости является так называемая идеальная жидкость, т.е. жидкость, лишенная внутреннего трения (вязкости). Считается, что по площадкам соприкасания двух друг относительно друга движущихся объемов действуют лишь нормальные к площадке силы давления и полностью отсутствуют лежащие в плоскости площадки касательные силы.

В механике жидкости для облегчения решения некоторых задач используется понятие о невязкой (совершенной) жидкости.

Под невязкой жидкостью понимают воображаемую жидкость, обладающую абсолютной подвижностью, т.е. лишенную вязкости, а также абсолютно несжимаемую, не расширяющуюся с изменением температуры, абсолютно неспособную сопротивляться разрыву. Таким образом, невязкая жидкость представляет собой некоторую модель реальной жидкости. Выводы, полученные исходя из свойств невязкой жидкости, приходится, как правило, корректировать, вводя поправочные коэффициенты.

Общей задачей кинематики является описание движения среды. Существуют два способа задания движения сплошной среды. Первый из них заключается в задании так называемых кинематических уравнений движения

(1)

Входящие сюда в качестве параметров величины , сохраняющие постоянные значения при движении среды, служат для указания выбора той точки среды, движение которой описывается уравнениями (1).Такого рода параметрами могут быть декартовы или криволинейные координаты точек среды в какой-то начальный момент времени. Совокупность величин: носит наименование переменных Лагранжа.

При лагранжевом задании движения среды проекции скоростей и ускорений точек среды определятся равенствами

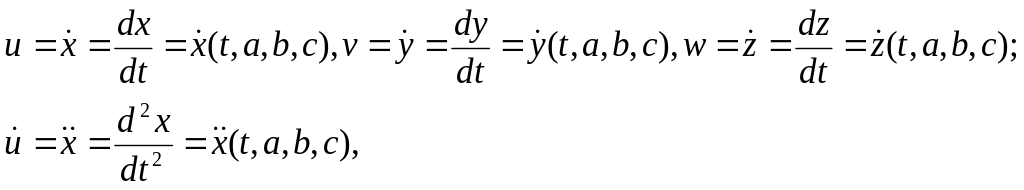(2)

Здесь точка над буквой – производная по времени проекции вектора скорости на оси прямоугольной декартовой системы координат; проекции вектора ускорения на те же оси.

Второй наиболее используемый способ задания сплошной среды – это способ Эйлера, заключающийся в задании поля скорости, т.е. зависимости проекций скорости от координат точек пространства и времени :

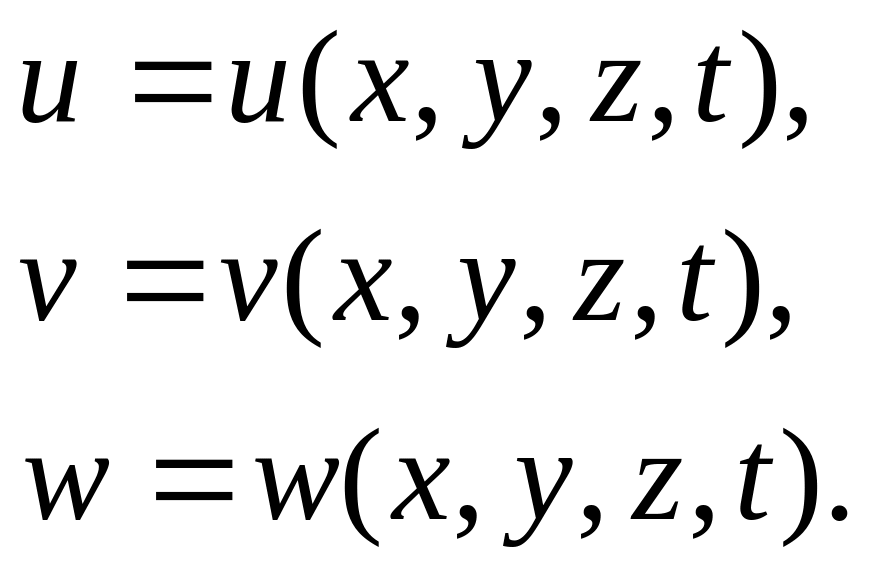(3)

Совокупность величин называют переменными Эйлера. Основное различие между этими двумя способами заключается в том, что в методе Лагранжа величины являются переменными координатами движущейся частицы жидкости, а в методе Эйлера – это координаты фиксированных точек пространства, мимо которых в данный момент времени проходят частицы жидкости.

Поле скоростей будет стационарным, т.е. не изменяющимся во времени, если в равенства (3) время не входит.

Поле скоростей (3) представляет собой бесконечное множество векторов скорости. Чтобы сделать это многообразие более обозримым, необходимо как-то упорядочить его рассмотрение. Для этого вводится представление о линиях тока в поле скоростей как о таких линиях, вдоль которых в данный момент времени векторы скорости направлены по касательным к ним в каждой точке.

О линиях тока даст наглядное представление следующий простой опыт. Насыпем на поверхность воды в канале легкий и хорошо видимый порошок, не растворяющийся в воде. Будем считать. Что частички порошка полностью увлекаются водой при ее движении, так что движения частиц воды и порошка на поверхности воды одинаковы (на самом деле это совсем не так; некоторая разница, особенно в тех областях, где движение воды резко ускоряется или замедляется, существует). При фотографировании с малым промежутком времени каждая частичка порошка изобразится на снимке в виде маленькой черточки. Черточки эти, соответствующие малым перемещениям частичек за время экспозиции сольются в отчетливо видимые линии, которые и будут представлять линии тока рассматриваемого движения.

Линии тока в жидкости при нестационарном поле скоростей не совпадают с траекториями ее частиц. Действительно, рассмотрим точку М жидкости, скорость которой в данный момент времени равна . Чтобы построить линию тока для выбранного момента времени, отступим вдоль вектора скорости в смежную точку , нанесем на чертеже скорость точки , отметим на этом векторе точку , близкую к , проведем вектор ее скорости и т.д. Полигон , если стороны его взять сколь угодно малыми, представит линию тока, проведенную через данную точку и в данный момент времени. Для построения траектории частицы жидкости, в данный момент времени, находящейся в точке , проследим за движением этой частицы с течением времени. За малый промежуток времени частица переместится вдоль вектора скорости из точки в положение , причем перемещение подбором промежутка времени можно при желании сделать равным произвольному малому отрезку линии тока. Скорость в точке уже не будет равна , так как за протекший малый промежуток времени, в силу нестационарности поля, скорость изменится и станет равной, например, . Т.о., траектория далее уже пойдет по направлению , а затем и т.д.; полигон представит траекторию частицы с тем меньшей ошибкой, чем меньшими будут выбираться промежутки времени. Из построения вытекает следующий результат: при нестационарности поля скоростей линии тока совпадают с траекториями частиц.

Проведем в данный момент времени в жидкости некоторый замкнутый, себя не пересекающий контур, контур . Через каждую точку такого контура можно провести определенную линию тока. Совокупность этих линий тока образует поверхность тока, а часть жидкости, выделенная из нее поверхностью тока, проведенной через замкнутый контур, называется трубкой тока. Проведя через контур поверхность , заключенную внутри трубки тока и опирающуюся на контур , получим сечение трубки. Если все линии тока, расположенные внутри трубки тока и на ее поверхности, нормальны к поверхности сечения, то такое сечение называют нормальным или ортогональным сечением трубки.

Лекция №3

Общие законы и уравнения гидростатики.

Силы, действующие в жидкостях. Гидростатическое давление. Общий случай напряженного состояния. Скорость деформации. Связь между напряженным состоянием и скоростью деформации.

В массе жидкости, которую мы рассматриваем как сплошную среду, под влиянием внешних сил возникают соответствующие внутренние силы. Проведем мысленно внутри рассматриваемой массы поверхность, разделяющую объем массы на две части и (рис. ). Отбросим одну из них, например ; часть остается в равновесии. Это значит, что во всех точках разделяющей поверхности нужно ввести такие же силы, с которыми масса действовала на массу .

На элементарной площади разделяющей поверхности действует сила . Площадь может быть стянута в точку с координатами . В этом случае как площадь поверхности так и сила стремятся к нулю. Отношение силы к площади поверхности стремится к пределу:

.

Значение этого предела называется напряжением в точке с координатами , возникающим на площади . Значение напряжения в одной и той же точке зависит от ориентации выбранной площадки, на которой оно возникает и может быть направлено по отношению к ней под определенным углом.

Оценим порядок значений сил, действующих на элементарный изолированный объем (рис. ), имеющий форму параллелепипеда со сторонами . Вся система движущейся массы отнесена к координатам . На плоскостях граней изолированного параллелепипеда возникают напряжения. Их можно разложить на составляющие: нормальную к грани и расположенную в плоскости грани, которые, в свою очередь, можно разложить на составляющие, параллельные соответствующим осям координат. Составляющие напряжений, направленные перпендикулярно грани, называются нормальными напряжениями. Составляющие, находящиеся в плоскости граней, называются касательными напряжениями.

В покоящихся жидкости и газе касательные напряжения в любой произвольной точке равны нулю и напряженное состояние определяется совокупным действием только нормальных напряжений, равных между собой ( ).

Напряжения и являются сжимающими, так как жидкости и газы не сопротивляются растягивающим усилиям. Величина, равная модулю напряжения , в МЖГ называется гидростатическим давлением в точке и обозначается буквой :

. (1)

Гидростатическое давление в точке также может быть представлено следующим образом. Рассмотрим в покоящейся жидкости произвольный объем , ограниченный поверхностью ; влияние жидкости, окружающей выделенный объем, можно заменить действием распределенных по поверхности сил , направленных по нормали к этой поверхности в каждой ее точке (рис. ).

Проведем секущую плоскость , делящую объем на две части и, и отбросим мысленно одну из них (например ). Действие отброшенной части на нижнюю часть следует заменить распределенными по поверхности силами , одна из них приходится на долю поверхности . Напряжение сжатия , возникающее при этом, определяется как частное от деления силы на площадь :

. (2)

Значение этого напряжения принято называть средним гидростатическим давлением; предел отношения (2) при называется гидростатическим давлением в точке:

. (3)

Размерность давления совпадает с размерностью напряжения.

Гидростатическое давление обладает двумя свойствами.

Первое свойство. Сила гидростатического давления направлена по внутренней нормали к площадке, которая воспринимает это давление. Действительно, если жидкость или газ находятся в равновесии, то в любой произвольной точке касательные напряжения равны нулю и перемещение жидкой частицы вдоль площадки невозможно, так как в противном случае равновесие нарушится. Совпадение же направления действия силы гидростатического давления с внутренней нормалью доказывается свойством жидкости или газа не оказывать сопротивления растягивающим усилиям.

Второе свойство. Величина гидростатического давления в точке не зависит от ориентации (от угла наклона) площадки.

Для доказательства этого свойства выделим в покоящейся жидкости элементарный объем в форме тетраэдра (рис. ).

Действие жидкости, окружающей тетраэдр, заменим действием поверхностных распределенных по его граням сил давления и массовой силы , определяемой массой тетраэдра. Для рассматриваемого объема запишем условия равновесия в виде трех уравнений проекций действующих сил и трех уравнений моментов:

(5)

Последнее условие (равенство нулю главного момента) удовлетворяется тождественно, так как при стягивании тетраэдра в точку ( ) равнодействующая всех внешних сил по отношению к выделенному объему сил проходит через центр тяжести этого объема.

Составим уравнение проекций внешних сил на ось . В соответствии с рис. 4 можно записать:

, (6)

где сила гидростатического давления на грань , сила гидростатического давления на грань ; элементарная массовая сила, пропорциональная массе тетраэдра.

Определим каждое слагаемое уравнения (6):

, (7) где среднее гидростатическое давление на грань , площадь которой равна ;

, (8) где проекция площадки (треугольник ) на плоскость ;

,

где масса элементарного тетраэдра; ускорение массовой силы.

(9)

где , соответственно проекции ускорения на оси координат.

После подстановки (7), (8) и (9) в исходное уравнение равновесия (6) имеем:

, (10)

или после сокращения на

. (11)

Пренебрегая величиной как бесконечно малой по сравнению с и , получаем: .

Обращаясь к условиям равновесия (4) в проекциях на и , по аналогии находим: и , откуда следует:

. (12)

Равенство (12) показывает, что гидравлическое давление на различных гранях тетраэдра с точностью до бесконечно малой величины постоянно. При стягивании тетраэдра в точку значения среднего гидростатического давления можно заменить гидростатическим давлением в точке. Следовательно, уравнение (12) показывает, что гидростатическое давление в точке одинаково по любому направлению, т.е. не зависит от того, как ориентирована площадка, воспринимающая это давление.

Положение элементарного тетраэдра было выбрано произвольно, поэтому можно заключить, что гидростатическое давление является непрерывной функцией координат пространства:

. (13)

Лекция №4. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера).

Выделим в покоящейся жидкости элементарный объем в форме прямоугольного параллелепипеда с ребрами, параллельными осям координат и равными соответственно (рис. ). Со стороны окружающей жидкости на выделенный параллелепипед действуют поверхностные силы, определяемые гидростатическим давлением, а также массовые силы, пропорциональные его массе.

Составим уравнение равновесия для этой системы сил в проекциях на координатную ось . При этом будем предполагать, что гидростатическое давление есть непрерывная функция координат пространства и что его значение в центре тяжести параллелепипеда (точка М) равно . Тогда первое уравнение равновесия в проекциях на ось запишется следующим образом:

(14)

где сила гидростатического давления на грань 1-2-3-4; то же на грань 5-6-7-8; проекция элементарной массовой силы на ось ; -- среднее гидростатическое давление соответственно на грани 1-2-3-4 и 5-6-7-8.

Так как гидростатическое давление является функцией координат, значения давлений и будут:

;

.

Тогда уравнение (1) примет вид:

(15)

или

. (16)

Проделав аналогичные операции с проекциями внешних сил на оси и , получим систему дифференциальных уравнений равновесия жидкости:

(17)

Эта система уравнений была впервые получена в 1755 году Эйлером.

Умножим каждое уравнение (17) соответственно на и сложим их:

(18)

или

(19)

Давление является функцией только трех независимых переменных координат , поэтому левая часть уравнения (19) представляет собой полный дифференциал функции . Следовательно,

(20)

Уравнение (20) называется основным дифференциальным уравнением равновесия жидкости. Это уравнение имеет общий характер и может быть использовано и для сжимаемой жидкости, так как мы не вводили никаких дополнительных ограничений на массовые силы и на плотность.

Левая часть уравнения (20) представляет собой полный дифференциал, значит, и правая его часть также должна быть полным дифференциалом.

Если принять плотность жидкости или газа постоянной или независимой от , то выражение в скобках тоже будет полным дифференциалом некоторой функции , частные производные которой, равны проекциям ускорений массовых сил на соответствующие оси:

(21)

Величины можно рассматривать как проекции массовых сил, отнесенных к единице массы данной жидкости, поэтому функцию называют потенциальной или силовой функцией, а силы, удовлетворяющие условию (21), - силами, имеющими потенциал. Таким образом, при рассмотрении уравнения (20) с учетом выражения (21) можно сделать вывод: равновесие жидкости возможно только в том случае, когда массовые силы имеют потенциал.

В основном уравнении равновесия жидкости неизвестны только две величины и .

Следовательно, для получения однозначного решения уравнения (20) нужно воспользоваться так называемым характеристическим уравнением, которое определяло бы связь между физическими свойствами и состоянием рассматриваемой жидкости, например, связь между плотностью жидкости, ее температурой и давлением.

Поверхность, в каждой точке которой значение данной функции постоянно, называется поверхностью уровня. В МЖГ наибольший интерес представляет поверхность равного давления, т.е. такая поверхность, в каждой точке которой давление имеет постоянное значение.

Уравнение поверхности равного давления просто получается из основного уравнения равновесия жидкости. так как для поверхности уровня в любой ее точке, и, следовательно, правая часть уравнения также равна нулю. Плотность жидкости отлична от нуля, поэтому выражение в скобках должно быть равным нулю:

(22)

Это и есть уравнение поверхности уровня.

Поверхность уровня обладает двумя основными свойствами: