Рекомендуемая литература Основная литература

1. Пискунов Н.С. Курс дифференциального и интегрального исчисления. М.: Наука. 1985. Т.1.

2. Пискунов Н.С. Курс дифференциального и интегрального исчисления. М.: Наука. 1985. Т.2.

3. Жевняк Р.М., Карпук А.А. Высшая математика. Мн.: Высш. шк. 1985-1987, ч.2, ч.3.

4. Красс М.С., Чупрынов Б.П. Основы математики и её приложения в экономическом образовании. М.: «Дело», 2001.

5. Рябушко А.П., Бархатов В.В., Державец В.В., Юруть И.Е. Индивидуальные домашние задания по высшей математике. Мн.: Высш. шк. 2000, ч.1 и ч.2.

6. Гусак А.Н. Высшая математика. Мн.: Тетра Системс 2000, ч.1 и ч.2.

7. Малыхин В.И. Математика в экономике. М.: ИНФРА-М, 2001.

Дополнительная литература

8. Высшая математика. Общий курс. Под общей редакцией С.А. Самаля. М.: Высшая школа, - 2000.

9. Лихолетов И.И., Мицкевич И.П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. Мн.: Вышэйшая школа, - 1976.

М одуль 1. Линейная алгебра

§ 1. Определители

О пределителем второго порядка называется величина, которая записывается в виде квадратной таблицы и задаётся равенством:

,

где — элементы определителя; индекс обозначает номер строки, а индекс — номер столбца, в котором находится элемент .

Пример 1.1.

Вычислите определитель второго порядка .

.

М инором элемента определителя называется определитель, обозначаемый символом , который получается из данного вычёркиванием строки и столбца, на пересечении которых стоит элемент .

А лгебраическим дополнением элемента определителя, обозначаемым , называется его минор, взятый со знаком плюс, если сумма номеров строки и столбца, на пересечении которых стоит элемент чётная, и со знаком минус в противном случае, т.е.

.

Пример 1.2.

А ) Найдите минор и алгебраическое дополнение элемента определителя .

Э лемент . Вычеркнем вторую строку и третий столбец: .

Тогда минор . Алгебраическое дополнение .

Б) Вычислите минор и алгебраическое дополнение элемента определителя .

Э лемент . Вычеркнем вторую строку и первый столбец: .

Т огда минор . Алгебраическое дополнение .

В примере 1.2 был найден определитель первого порядка.

О пределителем первого порядка называется величина, которая записывается в виде и которая равна значению .

Определителем третьего порядка называется величина, которая записывается в виде квадратной таблицы и задаётся равенством («разложение по элементам первой строки»):

т.е.

.

Замечание. В дальнейшем мы будем встречаться с кратким обозначением суммы:

Пример 1.3.

Вычислите определитель третьего порядка .

.

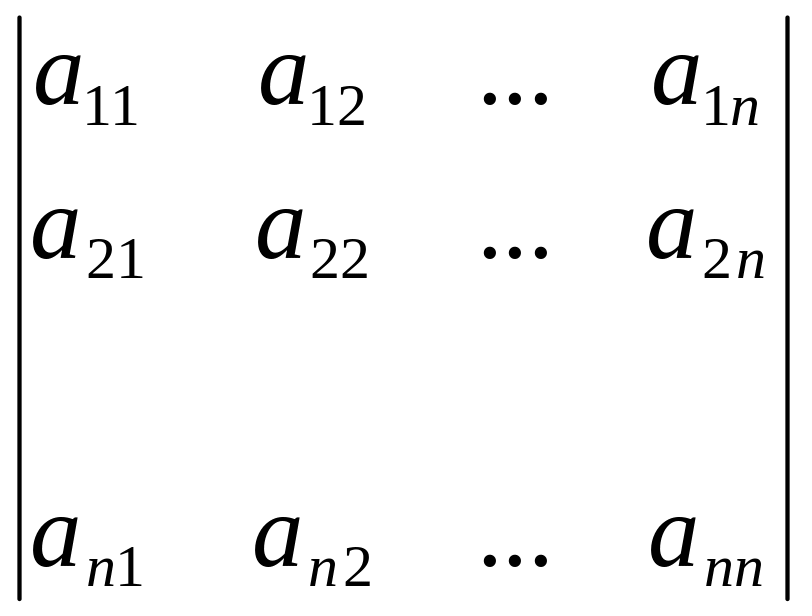О пределителем n-го порядка называется величина, которая записывается в виде квадратной таблицы и задаётся равенством («разложение по элементам некоторой строки или столбца»): определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

			разложение
		—	по элементам
			-той строки

			разложение
		—	по элементам
			-го столбца

Пример 1.4.

Вычислите определитель четвёртого порядка наиболее удобным способом:

.

Р азложим определитель по 4-ой строке:

.