
- •Isbn 978-985-519-056-2 © бгату, 2009 Предисловие
- •Учебная программа по учебной дисциплине
- •Модуль 4 Аналитическая геометрия
- •Модуль 8 Функции нескольких переменных
- •Рекомендуемая литература Основная литература
- •Дополнительная литература
- •М одуль 1. Линейная алгебра
- •§ 1. Определители
- •С войства определителей.
- •§ 2. Матрицы
- •§ 3. Основные операции над матрицами
- •§ 4. Транспонированная матрица
- •§ 5. Обратная матрица
- •§ 6. Ранг матрицы. Элементарные преобразования матрицы
- •Контрольный тест
- •Задачи для самостоятельного решения
- •§ 1. Теорема Кронекера-Капелли
- •§ 2. Решение систем линейных уравнений
- •Контрольный тест
- •Модуль 3. Векторная алгебра
- •§ 1. Векторы. Операции над ними.
- •Сложение векторов.
- •Произведение вектора на число.
- •§ 2. Декартовы прямоугольные координаты вектора. Длина вектора.
- •§ 3. Скалярное произведение векторов.
- •Свойства скалярного произведения.
- •Контрольный тест
- •М одуль 4.
- •§ 1. Прямая на плоскости.
- •3 . Уравнение прямой в отрезках:
- •6 . Уравнение прямой, проходящей через данную точку и с заданным угловым коэффициентом:
- •§ 2. Взаимное расположение прямых на плоскости.
- •§ 3. Прямые в решениях экономических задач.
- •5. Рівняння прямої, що проходить через дану точку в даному напрямку.
- •6. Рівняння прямої, що проходить через дану точку із заданим нормальним вектором.
- •8. Рівняння прямої, що проходить через дану точку із заданим напрямних вектором.
- •Модуль 5. Кривої другого порядку
- •§ 1. Окружність
- •§ 3. Гіпербола
- •§ 4. Порабола
- •М одуль 6. Функції однієї змінної. Безперервність функції однієї змінної.
- •§ 1. Визначення функції і способи її завдання
- •§ 2. Використання елементарних функцій в економіці
Модуль 5. Кривої другого порядку

§ 1. Окружність
Окружністю
називається безліч всіх точок площини,
віддалених від заданої точки
![]() цій же
площині на одне і теж відстань
цій же
площині на одне і теж відстань
![]() .
Точка
називаеться центром,
а
.
Точка
називаеться центром,
а
![]() —
радіусом
окружності.
У прямокутній системі координат
рівняння кола має вигляд
—
радіусом
окружності.
У прямокутній системі координат
рівняння кола має вигляд
![]() ,
(1)
,
(1)

де
![]() —
координати її
центру,
—
радіус кола.
—
координати її
центру,
—
радіус кола.
Зокрема,
якщо центр кола збігається з початком
координат, тобто
![]() ,
,
![]() ,
то рівняння
(1) прийме вигляд:
,
то рівняння
(1) прийме вигляд:
![]() (2)
(2)
Приклад
5.1.
Знайдіть координати центру і радіус
кола
![]() .
.
Розділивши
рівняння на 2, і згрупувавши члени
рівняння, отримаємо
![]() .
доповнимо вираження
.
доповнимо вираження
![]() і
і
![]() до повних квадратів,
додавши до першого двучленной 4, а до
другого
до повних квадратів,
додавши до першого двучленной 4, а до
другого
![]() (одночасно до правої частини додається
сума цих чисел):
(одночасно до правої частини додається
сума цих чисел):
![]()
![]() .
.
За
формулою
(1)
имеем
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() —
координати центра кола;
—
координати центра кола;![]() —
радіус кола.
—
радіус кола.
§ 2. Еліпс
Еліпсом
називається множина всіх точок площини,
сума відстаней від кожної з яких до двох
даних точок
![]() и
и
![]() цій же площині, званих фокусами еліпса,
є величина постійна і більша, ніж відстань
між фокусами.
Канонічне
рівняння еліпса
:
цій же площині, званих фокусами еліпса,
є величина постійна і більша, ніж відстань
між фокусами.
Канонічне
рівняння еліпса
:
![]() ,
(3)
,
(3)
де — велика піввісь, - Мала піввісь еліпса.

Якщо
 ,
то:
,
то:координати фокусів:
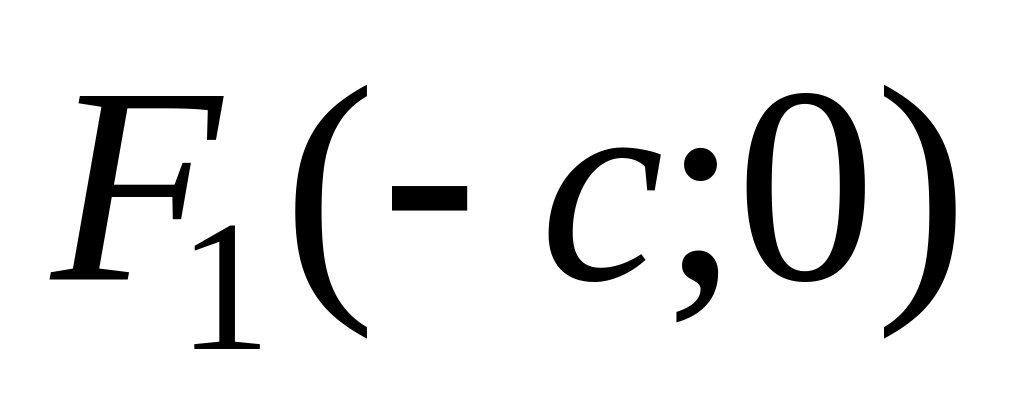 ,
,
 ,
де
,
де
 —
половина відстані
між фокусами (див. рис); числа
,
і
пов'язані співвідношенням
—
половина відстані
між фокусами (див. рис); числа
,
і
пов'язані співвідношенням
![]() ;
(4)
;
(4)
2)відстань
між фокусами дорівнює
![]() ;
;
. Форма еліпса характеризується його ексцентриситетом.
Эксцентриситетом
![]() еліпса називається
відношення фокусної відстані
еліпса називається
відношення фокусної відстані
![]() (відстані
між фокусами) до великої осі:
(відстані
між фокусами) до великої осі:
![]() :
:
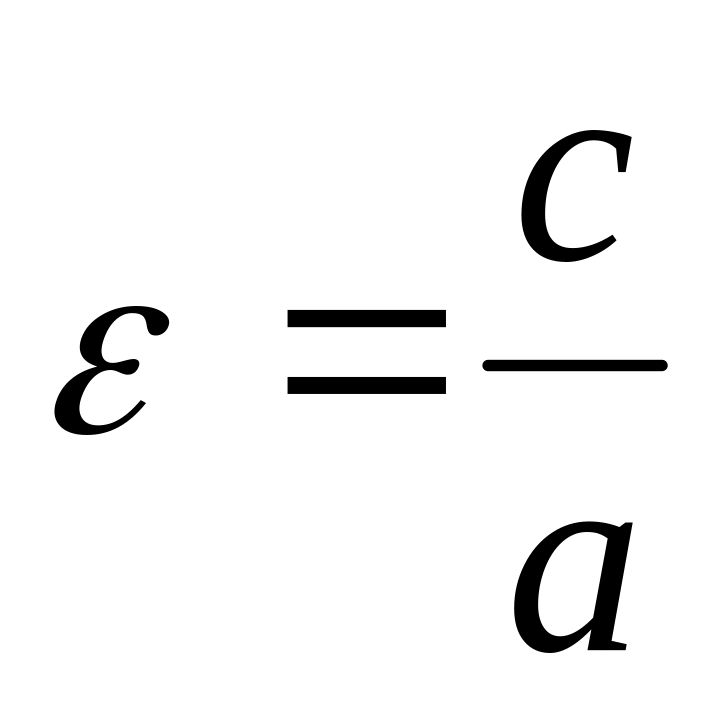 (
( ,
т.к.
,
т.к.
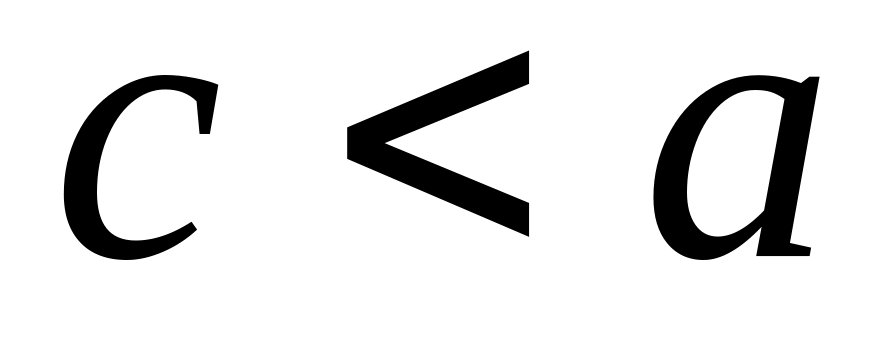 );
(5)
);
(5)
Д
иректрисами
еліпса
називаються прямі и
![]() паралельні
малої осі еліпса і віддалені від неї на
відстані, рівному
паралельні
малої осі еліпса і віддалені від неї на
відстані, рівному
![]() ;
;
 и
и
 —
рівняння
директрис.
—
рівняння
директрис.
Якщо
 ,
то рівняння (3) визначає
коло
,
то рівняння (3) визначає
коло
 .
.
Приклад
5.2.
Данно рівняння еліпса
![]() .
Знайдіть довжини його піввісь, координати
фокусів, ексцентриситет еліпса.
.
Знайдіть довжини його піввісь, координати
фокусів, ексцентриситет еліпса.
Запишемо
рівняння еліпса у вигляді (3), розділивши
обидві його частини на 1176:![]() .
.
Звідси
![]() ,
,
![]() .
.
Використовуючи
співвідношення (4), знаходимо
![]() і
і
![]() .
Отже,
.
Отже,
![]() и
и
![]() .
.
За
формулою
(5)
находим
![]() .
.
§ 3. Гіпербола
Гіперболой називається множина всіх точок площини, модуль різниці відстаней від кожної з яких до двох заданих точок и цій же площині, званих фокусами, є величина постійна, менша, ніж відстань між фокусами.
Канонічне рівняння гіперболи:
![]() ,
(6)
,
(6)
де
—
дійсна,
— уявна
піввісь гіперболи.
Числа
![]() і
і
![]() —
відповідно дійсна
і уявна осі гіперболи. Для гіперболи
(6):к
оординати
фокусів:
,
,
де
—
половина відстані між фокусами (см.
рис);
—
відповідно дійсна
і уявна осі гіперболи. Для гіперболи
(6):к
оординати
фокусів:
,
,
де
—
половина відстані між фокусами (см.
рис);
числа , і звязані відношенням
![]() ;
(7)
;
(7)
відстань між фокусами дорівнює ;
точки и називаються вершинами гіперболи , точка — центром гіперболи;

![]()
Эксцентриситетом гіперболи називаеться число:
5
)
(![]() ,
т.к.
,
т.к.
![]() ).
(8)
).
(8)
. Прямокутник, центр якого збігається з точкою О, а сторони рівні і паралельні осях гіперболи, називається основним прямокутником гіперболи.
Діагоналі основного прямокутника гіперболи лежать на двох прямих, званих асимптотами гіперболи они определяются уравнениями
6)
![]() (9)
(9)
Д
ві
прямі
![]() і
(див. мал), паралельні
уявної осі гіперболи і віддалені від
неї на відстані, рівному
,
називаються
директрисами
гіперболи;
вони визначаються рівняннями 7)
і
(див. мал), паралельні
уявної осі гіперболи і віддалені від
неї на відстані, рівному
,
називаються
директрисами
гіперболи;
вони визначаються рівняннями 7)
![]() .
(10)
.
(10)
Р
івняння
![]() або
або
![]() (11)
(11)
також
є рівнянням гіперболи, але дійсною віссю
цієї гіперболи служить відрізок осі
довжини
![]() .
.
Гіпербола, що задається рівнянням (11), називається сполученої гіперболи (6)
Пример 5.3. Складіть рівняння гіперболи, якщо її фокуси лежать на осі і відстань між ними дорівнює 10, а довжина уявної осі дорівнює 8.
За
умовою,
![]() ;
;
![]() .
Тоді за формулою (7) отримаємо:
.
Тоді за формулою (7) отримаємо:![]() .
.
Тоді рівняння гіперболи:
![]() .
.
Рівняння:![]() ,
,
![]() також задають гіперболу, координати
центру якій задаються точкою
також задають гіперболу, координати
центру якій задаються точкою
![]() .
.
