2. Пружинный маятник

П

, (12.2)

где k – жесткость пружины

x – перемещение груза.

а) Уравнение движения пружинного

маятника

По второму закону Ньютона: ma = F

или (12.3)

Т.е. пружинный маятник совершает гармонические колебания по закону

,

ружинный маятник – это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы.

где , тогда , а период: (12.4)

б) Потенциальная энергия пружинного маятника

(12.5)

Учитывая, что ,

Если на маятник действует сила трения, пропорциональная скорости

,

где , а - коэффициент сопротивления, то колебания маятника будут затухающими и закон движения маятника будет иметь вид:

, (12.6) (12.7)

Уравнение затухающих колебаний имеет вид ,

очевидно, что , а . Смысл этих параметров будет рассмотрен позже в разделе «Затухающие колебания».

3. Математический маятник

М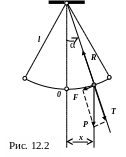 атематическим маятником называется идеализированная система, состоящая из материальной точки массой m , подвешенной на невесомой нерастяжимой нити длиной l , и колеблющейся под действием силы тяжести без трения.

Хорошей моделью математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити.

При малых углах отклонения (маятник на большие углы не отклоняется) α можно считать .

Составляющая F силы тяжести P, направленная перпендикулярно линии подвеса, называется возвращающей силой.

Возвращающая сила математического маятника:

.

Поскольку возвращающая сила стремиться уменьшить x:

(12.8)

Уравнение движения:

или (12.9)

Следовательно, движение математического маятника описывается дифференциальным уравнением гармонических колебаний то есть происходит по закону , где (12.10); (12.11)

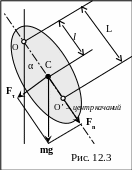
4. Физический маятник

Физическим маятником называется твердое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси подвеса, не проходящей через центр масс тела.

Если физический маятник отклонен от положения равновесия на некоторый угол α, то момент возвращающей силы:

(12.12)

C другой стороны, при малых углах

(12.13)

Где: J – момент инерции маятника относительно оси, проходящей через точку подвеса О.

l – расстояние между точкой подвеса и центром масс С маятника.

– возвращающая сила (- т.к. она всегда противоположна направлению увеличения угла α. Следовательно:

(12.14) или (12.15)

Таким образом, при малых колебаниях физический маятник также является гармоническим осциллятором и совершает гармонические колебания с циклической частотой ω. Решением уравнения (12.5) является выражение:

(12.16)

Циклическая частота и период колебаний:

(12.17), (12.18)

Приведенная длина физического маятника:

- уравнение математического маятника

(12.19), тогда:

Приведенная длина физического маятника – это длина такого математического маятника, который имеет тот же период колебаний, что и данный физический маятник.

Точка О’ на продолжении прямой ОС, отстоящая от оси подвеса на L, называется центром качаний физического маятника.

Применяя теорему Штейнера, получим:

Т.е. приведенная длина L физического маятника всегда больше длины l эквивалентного математического маятника (ОО’ всегда больше ОС).

Точка подвеса О и центр качаний О’ обладают свойством взаимозаменяемости: если точку подвеса перенести в центр качаний, то прежняя точка О станет новым центром качаний, и период колебаний физического маятника не изменится.

Математический маятник является частным случаем физического маятника, если предположить, что вся его масса сосредоточена в центре масс, а приведенная длина физического маятника – это длина такого математического маятника, у которого период колебаний совпадает с периодом колебаний физического маятника.