3. Механика твердого тела

1. Момент инерции. Теорема Штейнера

Момент инерции

Моментом инерции тела (механической системы) относительно оси вращения есть физическая величина, равная сумме произведений масс n материальных точек на квадраты их расстояний до рассматриваемой оси:

В случае непрерывного распределения масс эта сумма сводится к интегралу, где интегрирование производится по всему объему тела. Величина r в данном случае есть функция положения точки с координатами x, y, z:

В качестве примера найдем момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис.7.1):

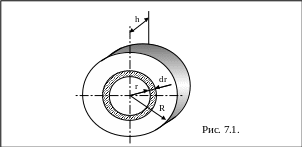
Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r + dr.

Теорема Штейнера

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:

Момент инерции тела J относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси, проходящей через центр масс тела С, сложенному с произведением массы тела m на квадрат расстояния а между осями:

Моменты инерции однородных тел , имеющих массу m, равномерно распределенную по объему, и правильную геометрическую форму:

Тело	Положение оси вращения	Момент инерции
Труба (полый тонкостенный цилиндр) радиуса R	Ось симметрии
Цилиндр сплошной или диск радиуса R	Ось симметрии
Стержень прямой тонкий, длиной l	Ось перпендикулярна стержню и проходит через его середину
Шар радиусом R	Ось проходит через центр шара

Пример: Найти момент инерции стержня длиной l относительно оси, которая перпендикулярна стержню и проходит через его конец (т.е. ).

Таким образом, величина момента инерции зависит от выбора оси вращения. Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

Момент силы

Момент силы относительно неподвижной точки О

- называется физическая величина, определяемая векторным произведением радиуса-вектора , проведенного из точки О в точку А приложения силы, на силу (см. рисунок 7.3.):

З десь - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Модуль момента силы:

, где

- угол между и ;

- плечо силы - кратчайшее расстояние между линией действия силы и точкой О.

Момент силы относительно неподвижной оси Z

М оментом силы относительно неподвижной оси Z называется скалярная величина , равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки О данной оси Z (Рис.7.4).

Рис. 7.4.

Значение момента не зависит от выбора положения точки О на оси Z.

КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩЕНИЯ

Уравнение динамики вращательного движения

твердого тела

Абсолютно твердое тело вращается около неподвижной оси Z , проходящей через него (Рис. 7.5). Все точки тела движутся с одинаковой угловой скоростью . Разбивая тело на элементарные объемы массами

m₁,m ₂, … m_n, находящиеся от оси на расстояниях r₁, r₂, … r_n , получим выражение для кинетической энергии вращения всего тела.

Кинетическая энергия вращения

:

где - момент инерции тела относительно оси Z.

Из сравнения формул и следует, что момент инерции – мера инертности тела при вращательном движении.

Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна сумме кинетических энергий этих движений:

Уравнение динамики вращательного движения

Для вывода уравнения динамики вращательного движения твердого тела рассмотрим элементарную работу вращения, которая идет на увеличение его кинетической энергии:

, в свою очередь , тогда

, делим на dt: , окончательно:

В векторном виде: ,

где - главный момент инерции тела (момент инерции относительно главной оси).

Момент импульса и закон его сохранения

Моментом импульса (количества движения) L материальной точки А относительно неподвижной точки О (рис. 7.6) называется физическая величина, определяемая векторным произведением:

,

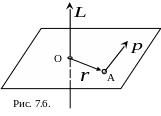Модуль момента импульса:

Моментом импульса относительно неподвижной оси Z называется скалярная величина L_z , равная проекции на эту ось вектора момента импульса относительно точки О, принадлежащей этой оси. - псевдовектор.

Значение момента импульса L не зависит от положения точки на оси Z. При вращении твердого тела вокруг неподвижной оси, каждая точка тела движется по окружности постоянного радиуса со скоростью перпендикулярной радиусу. Момент импульса отдельной частицы равен: и направлен по оси в сторону, определяемую правилом правого винта (совпадает с направлением вектора угловой скорости ).

Момент импульса твердого тела

Моментом импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:

Продифференцируем по времени:

В векторной форме: - еще одна форма