2. Соударение

7. Условия равновесия механической системы.

Потенциальная кривая. Условия равновесия.

Потенциальный барьер, потенциальная яма.

Рассмотрим движение материальной точки в одной плоскости (рис.6.3). Это означает, что ее положение может быть определено с помощью одной величины, например координаты x.

В качестве примера можно привести шарик, скользящий без трения по изогнутой в вертикальной плоскости проволоке. Аналогичным примером может служить прикрепленный к концу пружины шарик, скользящий без трения по горизонтальной направляющей (рис. 6.3.а).

а)

На шарик действует консервативная сила: в первом случае – сила тяжести, во втором – упругая сила деформируемой пружины. На графиках представлены потенциальные кривые – зависимости потенциальной энергии от перемещения U(x).

Поскольку шарики движутся без трения, сила реакции опоры перпендикулярна вектору скорости шарика, поэтому работы над шариком не совершает. Следовательно, имеет место сохранение энергии:

8. Удар (соударение)

ОПРЕДЕЛЕНИЯ:

Удар – столкновение двух или более тел, при котором взаимодействие длится очень короткое время.

Центральный удар – удар, при котором тела до удара движутся вдоль прямой, проходящей через их центры масс. В настоящем курсе рассматриваются только центральные удары.

Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций, и нет потерь кинетической энергии.

Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело.

1. Абсолютно упругий удар

В случае прямого центрального удара (Рис. 6.1.) траектории тел после взаимодействия не меняются – они по-прежнему движутся вдоль прямой, проходящей через их ценры масс.

Обозначим , - массы и скорости тел до удара - скорости тел после удара.

Запишем выражения для законов сохранения импульса и энергии:

;

Избавимся от знаменателя во втором уравнении и сгруппируем члены чтобы найти скорости тел после удара:

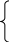распишем разности квадратов:

(1)

(2)

Подставляя (1) в (2), получим:

, (3)

Выразим из (3) : , (4)

из (1) выразим : и подставим в (4) и найдем скорости тел после удара. :

аналогично (5,6)

2. Абсолютно неупругий удар

Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое тело.

Согласно закону сохранения импульса:

, где - скорость тел после удара.

(8)

Если шары двигались навстречу друг другу, то вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий бóльшим импульсом. В частном случае, если массы шаров раны, то

при (9)

В случае неупругого удара закон сохранения кинетической энергии не соблюдается. Вследствие удара происходит пластическая деформация тел и переход части механической энергии в тепловую или другие виды энергии.

Эту потерю можно оценить как разность кинетической энергии до и после удара:

подставим сюда (8):

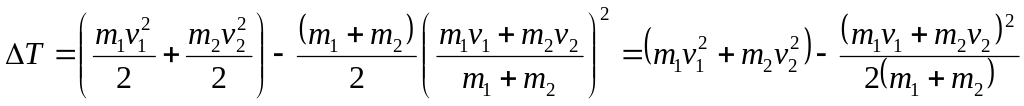
После преобразований получим выражение для потери кинетической энергии в результате абсолютно неупругого удара:

(10)

Если ударяемое тело было неподвижно , то:

, (11,12)

Если , то и , т.е. почти вся кинетическая энергия при неупругом ударе переходит в другие виды энергии. Поэтому для получения значительной деформации наковальня должна быть массивнее молотка.

ПРИМЕР:

Абсолютно упругий удар можно рассмотреть на примере установки, схема которой изображена на рисунке. Два шара массами m₁ и m₂ подвешены на расстоянии l от точки подвеса. Положения шаров в процессе эксперимента (до и после столкновения) определяются углами α_i .

Применяя закон сохранения импульса к проекциям импульсов шаров на горизонтальное направление, получим для упругого удара соотношение:

,

учитывая, что шар m₂ в начальном положении был неподвижен ( ):

,

или

2

1

В исходном положении шар 1 отклонен на угол α₀, а его ц.м. поднят на высоту Δh₀ . При этом потенциальная энергия шара меняется на величину

Если в системе нет потерь энергии, то при изменении угла от α₀ до 0 кинетическая энергия шара 1 меняется от 0 до П:

,

откуда скорость в момент удара: .

Так, как , то окончательно формула для скорости шаров определится выражением:

,

тогда выражения для импульсов:

, , .

Задавшись начальными условиями, найдем импульсы шаров после удара. Н.У.: m₁ = 0,5кг; m₂ = 0,2кг; l = 1м, .

1) Скорость первого шара до удара:

.

2) Импульс первого шара до удара: .

Импульс второго шара до удара равен нулю, т.к. он покоится (v₂ = 0).

3) Скорость 1-го шара после удара:

.

4) Скорость 2-го шара после удара:

,

5) Проверим закон сохранения импульса замкнутой механической системы:

, ч.т.д.