6 .Теплоемкость

Теплоемкость тела – это кол. тепла, необх. для нагревания его на 1К.

6.1. Удельная теплоемкость вещества с — величина, равная количеству теплоты, необходимому для нагревания 1кг вещества на 1 К.

Единица удельной теплоемкости — Дж/(кг К)

6.2.Молярная теплоемкость с_μ — величина, равная коли­честву теплоты, необходимому для нагревания 1моль вещества на 1К. Единица молярной теплоемкости — Дж/(моль К).

Связь между с_μ и с: с_μ = с·М

Различают теплоемкости (удельную и молярную) при постоянном объеме (с_v и С_v ) и при постоянном давлении (с_р и С_Р), если в процессе нагревания вещества его объем или давление поддерживаются постоянными.

6.2.1. Молярная теплоемкость при постоянном объеме (cv)

Из первого начала термодинамики dQ = dU + dA,

с учетом и ,

для 1 моля газа получим:

При V = const работа внешних сил δΑ равна нулю и сообщаемая газу извне теплота идет только на увеличение его внутренней энергии (dV_μ = 0).

C_v равна изменению внутренней энергии одного моля газа при повышении его температуры на 1 К.

Поскольку dU_μ = 1/2RdT, то C_v = i/2∙R

Если то , тогда или

6.2.2. Молярная теплоемкость при постоянном давлении (Cp ).

Уравнение Майера

Если газ нагревается при p = const, то

не зависит от вида процесса (внутренняя энергия идеального газа dU не зависит ни от р, ни от V, а определяется только Т) и всегда равна C_v.

Дифференцируя уравнение Клапейрона-Менделеева pV_µ = RT по Τ при

p = const, получим

C_p=С_V +R — уравнение Майера

С_p всегда больше С_V на величину универсальной газовой постоянной.

Это объясняется тем, что при нагревании газа при постоянном давлении требуется еще дополнительное количество теплоты на совершение работы расширения газа, так как постоянство давления обеспечивается увеличением объема газа.

П ри рассмотрении термодинамических процессов важную роль играет величина

которая называется коэффициентом Пуассона.

7. Работа при изопроцессах

Изопроцессы – это равновесные процессы, происходящие с термодинамическими системами, при которых один из основных параметров состояния сохраняется постоянным.

7.1. Изохорный процесс (V = const)

Диаграмма этого процесса — изохора — в коор­динатах (p,V) изображается прямой, параллельной оси ординат (ось p). Процесс 2-1 — изохорный нагрев, процесс 2-3 — изохорное охлаждение. При изохорном процессе газ не совершает работу над внешними телами (δΑ = pdV = 0) и вся теплота, сообщаемая газу, идет на увеличение его внутренней энергии (δQ = dU). Поскольку dUμ = Cv·dT, то для произвольной массы газа:

7.2. Изобарный процесс (р = const)

Диаграмма этого процесса — изобара — в координатах (p,V) изобра­жается прямой параллельной оси абсцисс (ось V). При изобарном процессе работа газа при увеличении объема от Vl до V2 равна: и определяется площадью заштрихованного прямоугольника.

Используя уравнение Менделеева-Клайперона

, получаем ,

о тсюда , или .

Физический смысл универсальной газовой постоянной R:

R численно равна работе изобарного расширения 1моля идеального газа при нагревании его на 1 К.

7.3. Изотермический процесс (Т = const)

Диаграмма этого процесса — изотерма — в коор­динатах (p,V) представляет собой гиперболу. Изотермический процесс описывается законом Бойля-Мариотта (pV = const). Работа изотермического расширения газа:

Так как при T = const внутренняя энергия идеального газа не изменяется, то из первого начала термодинамики следует, что δQ = δA, то есть все количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил.

Поэтому, для того, чтобы при расширении газа температура не понижалась, к газу в течение изотермического процесса необходимо подводить количество теплоты, эквивалентное внешней работе расширения.

8. Адиабатический процесс (δQ = 0).

Адиабатическим называется процесс, при котором отсутствует теплообмен между системой и окружающей средой (δQ = 0).

К адиабатическим процессам можно отнести все быстропротекающие процессы (теплообмен не успевает совершиться), например, распространение звука в среде, циклы расширения и сжатия в двигателях внутреннего сгорания, в холодильных установках и т. д.

Из первого начала термодинамики следует, что при адиабатическом процессе

Используя и , получим

(1)

C другой стороны, из следует (2)

Разделив (2) на (1) получим:

или , (3)

где - коэффициент Пуассона. Интегрирование уравнения (3) дает

Откуда следует уравнение Пуассона – уравнение адиабатического процесса:

и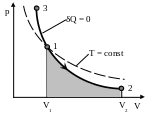 спользуя уравнение Менделеева-Клайперона , получаем:

Диаграмма адиабатического процесса – адиабата - в координатах (p,V) изображается гиперболой.

Адиабата (pV^γ = const) более крута, чем изотерма (pV = const). Это объясняется тем, что при адиабатическом сжатии (1 – 3) увеличение давления газа обусловлено не только уменьшением его объема, но и повышением температуры.