6. Работа в поле тяготения. Потенциал поля тяготения

Работа в поле тяготения по перемещению тела массой m на расстояние :

где: М – масса Земли

R – расстояние от Земли (см. рис.10.3)

Знак минус появляется потому, что сила F и перемещение dR в данном случае противоположны по направлению (см. рис.10.3).

Если тело перемещать с расстояния R₁ до R₂ , то работа А:

.

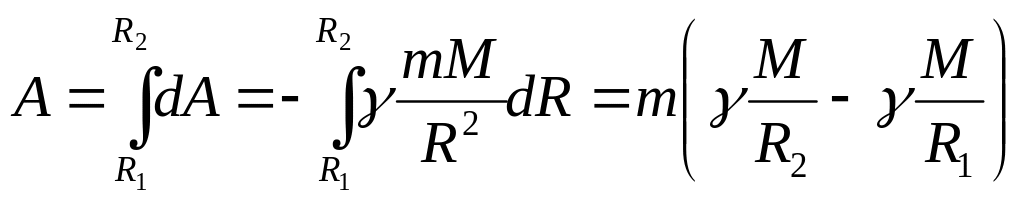
Из формулы А вытекает, что работа в поле тяготения не зависит от траектории перемещения, а определяется начальным и конечным положениями тела.

То есть силы тяготения действительно консервативны, а поле тяготения является потенциальным.

Т.к. работа, совершаемая консервативными силами, равна изменению потенциальной энергии системы, взятому с обратным знаком, то:

или

При потенциальная энергия П₂ = 0.

Поскольку первая точка выбрана произвольно, потенциальная энергия поля тяготения

П отенциал поля тяготения:

Величина является

энергетической характеристикой поля тяготения и называется

потенциалом поля тяготения.

Потенциал поля тяготения φ – скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля, или

работой поля по перемещению единичной массы из данной точки поля в бесконечность.

Взаимосвязь между потенциалом (φ) и напряженностью (g) поля тяготения:

(вытекает из полученного выше)

С другой стороны (dl – элементарное перемещение)

т.е. , откуда

7.Потенциальная энергия тела, находящегося на высоте h:

В качестве примера рассмотрим потенциальную энергию тела, находящееся на высоте h относительно Земли:

,

где R₀ – радиус Земли.

Так как и , то, учитывая, что h << R₀ , получаем: Таким образом, мы вывели формулу, которую ранее использовали как постулат.

8. Космические скорости

Д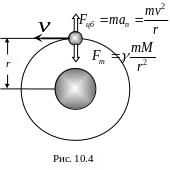 ля запуска космических объектов им необходимо придать соответствующие скорости для преодоления сил земного притяжения. Эти скорости называют космическими.

а) Первая космическая скорость (круговая)

– скорость вывода объектов на траекторию спутника Земли.

Первой космической скоростью называют такую минимальную скорость, которую надо сообщить телу, чтобы оно могло двигаться вокруг Земли по круговой орбите, т.е.

превратиться в искусственный спутник Земли.

На спутник, движущийся по круговой орбите радиусом r, действуют сила тяготения Земли и центробежная сила:

; .

Указанные силы равны и направлены в противоположные стороны (иначе тело сойдет с орбиты). Основываясь на этом, найдем первую космическую скорость:

, откуда: , здесь учтено - ускорение свободного падения кг·м/с. Если тело движется вблизи поверхности Земли, то можно принять (R_экв = 6378 км), тогда

м/с.

б) Вторая космическая скорость:

Вторая космическая скорость (параболическая) – скорость, необходимая объекту для преодоления силы притяжения Земли и выхода на орбиту спутника Солнца. Для достижения второй космической скорости необходимо, чтобы кинетическая энергия тела была равна работе, совершаемой против сил тяготения:

, откуда:

км/с

в) Третья космическая скорость – скорость покидания Солнечной системы:

v₃ = 16,7 км/с.

___________________________

Конец 4 лекции