ФЕДЕРАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

Липецкий государственный технический университет

Кафедра физики

и биомедицинской техники

Лекция № 04

(вводная)

по разделу «Механика»

учебного курса «Общая физика»

1. Деформация твердого тела

1. Закон Гука.

2. Потенциальная энергия упруго растянутого стержня.

3. Диаграмма напряжений.

2. Элементы теории поля.

4. Введение в теорию поля.

5. Поле центральных сил.

6. Законы Кеплера.

7. Закон всемирного тяготения.

8. Сила тяжести, вес, невесомость.

9. Поле тяготения, его напряженность.

10. Работа в поле тяготения.

11. Потенциал поля тяготения.

12. Потенциальная энергия тела на высоте h.

13. Космические скорости.

Составил: _____________ Т.А.Герасименко

Липецк – 2014

1. Деформации твердого тела

Реальные тела не являются абсолютно упругими.

Деформация — это изменение формы и размеров твердых тел под действием внешних сил.

Пластическая деформация — это деформация, которая сохраняется в теле после прекращения действия внешних сил.

Упругая деформация – если после прекращения действия внешних сил тело принимает первоначальные размеры и форму.

Все виды деформаций (растяжение, сжатие, изгиб, кручение, сдвиг) могут быть сведены к одновременно происходящим деформациям растяжения (или сжатия) и сдвига.

Напряжение — физическая величина, численно равная упругой силе , приходящейся на единицу площади сечения тела.

.

Если сила направлена по нормали к поверхности, то напряжение нормальное, если — по касательной, то напряжение тангенциальное.

Относительная деформация — количественная мера, характеризую­щая степень деформации и определяемая отношением абсолютной деформации Δх к первоначальному значению величины х, характеризующей форму или размеры тела, так:

— относительное изменение длины стержня (прод. деф.):

— относительное поперечное растяжение (сжатие) ,

где d —диаметр стержня.

Деформации и всегда имеют разные знаки: ,

где — коэффициентом Пуассона – положительный коэффициент, зависящий от свойств материала.

2. Закон Гука

Для малых упругих деформаций относительная деформация пропорциональна напряжению :

где — модуль упругости - коэффициент пропорциональности, численно равный напряжению, которое возникает при относительной деформации, равной единице.

Для случая одностороннего растяжения (сжатия) модуль упругости называется

модулем Юнга.

З

- Закон Гука

аписав , получим:

Здесь — коэффициент упругости.

Закон Гука: Удлинение стержня при упругой деформации

пропорционально действующей на стержень

силе.

Закон Гука выполняется только для упругих деформаций.

3. Связь между деформацией и напряжением

Диаграмма напряжений

Диаграмма напряжений – это график зависимости напряжения , возникающего в деформируемом теле от относительной деформации .

На рис. 9.6. он приведен для металлического образца. Из рисунка видно, что линейная зависимость , установленная Гуком, выполняется лишь в очень узких пределах, до так называемого предела пропорциональности ( ).

При дальнейшем увеличении напряжения деформация еще упругая (но уже не линейная) – до предела упругости ( ) остаточные деформации не возникают.

За пределом упругости в теле возникают остаточные деформации. При снятии напряжения в точке С график, описывающий возвращения тела в первоначальное состояние изображается прямой CF.

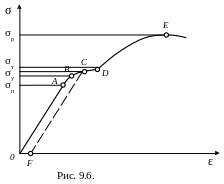
Точка С – соответствует пределу текучести ( ). В области CD деформация возрастает без увеличения напряжения, т.к. тело как бы «течет». Эта область называется областью текучести или пластической деформации. Материалы, для которых область текучести значительна, называются вязкими, а для которых она практически отсутствует – хрупкими.

При дальнейшем растяжении тела (после точки D) происходит его разрушение. Максимальное напряжение в теле, при котором происходит его разрушение, называется пределом прочности ( ).