7. Движение тел переменной массы. Формула Мещерского

Примером тел переменной массы может служить вращающаяся катушка с кабелем, масса которой увеличивается или уменьшается в зависимости от того, наматывается на нее кабель или сматывается.

Типичным примером движения тел переменной массы может служить полет ракеты на активном участке траектории, т.к. в процессе работы ее двигателя топливо сгорает, а продукты сгорания выбрасываются через сопло. Масса ракеты, таким образом, постепенно уменьшается.

Изменение импульса тела переменной массы за время dt :

,

где - импульс тела в момент времени ,

- импульс тела в начальный момент времени t, тогда

.

здесь: m и v – масса и скорость тела в момент времени t;

dm и dv – их изменения за малый промежуток времени dt;

v₁ – скорость отделяющихся частиц.

Если частицы отделяются, то их общая масса dm < 0. Выполнив преобразования и отбросив член dm·dv как малый высшего порядка малости по сравнению с остальными, получим:

или ,

где - относительная скорость отделяющихся частиц.

Подставляя последнее уравнение в закон изменения импульса , получим формулу Мещерского:

8. Реактивная сила. Формула Циолковского

Реактивная сила

Векторная величина

называется реактивной силой.

Полагая в формуле Мещерского отсутствие внешних сил, получим:

Если скорость ракеты и струя истекающих газов направлены в разные стороны, можно записать то же уравнение в скалярном виде:

, или

Формула Циолковского. Характеристическая скорость ракеты.

Если m₀ – стартовая масса ракеты, а m_Т – масса топлива, то максимальная скорость ракеты может быть найдена путем интегрирования:

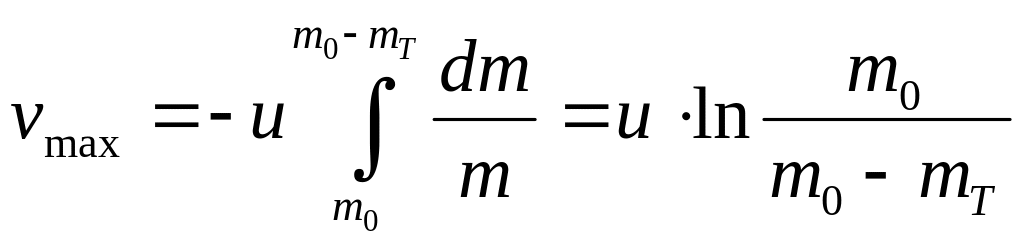
Эта формула получена К.Э. Циолковским, а скорость v_max – называется характеристической скоростью ракеты.

____________________________

конец 2 лекции