2. Кинематика

2.1. Определения

Механическое движение

Любое механическое движение относительно. В природе нет неподвижных тел и, значит, нет такого «удобного» тела, относительно которого можно было бы рассматривать все движения.

Исследователь вправе пользоваться любым из тел, условно считая его неподвижным, для рассмотрения движения других тел.

Телом отсчета называется тело, принятое за неподвижное.

Системой отсчета называют совокупность тела отсчета и связанной с ним системы координат. Движение происходит как в пространстве, так и во времени. Поэтому для описания движения необходимо также определять и время. Это делается с помощью часов.

2.2. Кинематика движения материальной точки

Движение тел происходит в пространстве и во времени. Поэтому для описания движения материальной точки надо знать, в каких местах пространства эта точка находилась и в какие моменты времени она проходила то или иное положение (по какой траектории двигалась).

Траектория – линия, описываемая материальной точкой (или телом) при движении относительно выбранной системы отсчета.

Траектории одного и того же движения тела в разных системах отсчета могут быть различными.

В зависимости от формы траектории различают:

• прямолинейное движение,

• криволинейное движение,

• поступательное движение,

• вращательное движение.

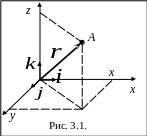
Радиус-вектор и координаты

Положение материальной точки (·) М в пространстве в данный момент времени может быть задано радиусом-вектором или тремя координатами x, y, z (Рис.3.1.).

Радиусом-вектором некоторой точки называется вектор, проведеный из начала координат в эту точку. Его проекции на координатные оси равны декартовым координатам данной точки:

r_x = x, r_y = y, r_z = z,

Следовательно, радиус вектор можно представить в виде

,

где – единичные векторы (орты) соответствующих осей системы координат. Соответственно r² = x² + y² + z².

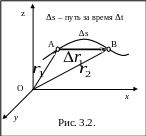
При движении материальной точки ее координаты с течением времени изменяются (рис. 3.2). В общем случае ее движение определяется системой скалярных уравнений

x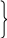 = x(t),

y = y(t), (1)

z = z(t),

эквивалентной векторному уравнению . (2)

Уравнения (1) и (2) называют кинематическими уравнениями движения материальной точки.

Вектор перемещения – вектор разности радиус-векторов конечного и начального положения движущейся точки за рассматриваемый промежуток времени Δt.

Длина пути ∆s – длина участка траектории AB, пройденного точкой за данный промежуток времени: ∆s = ∆s(t) – скалярная функция времени.

3. Прямолинейное движение

При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории и модуль перемещения |∆r| равен пройденному пути .

Если все точки траектории лежат в одной плоскости, движение называют плоским.

Скорость – векторная величина, которая определяет быстроту и направление движения в данный момент времени.

Средняя скорость (3) – векторная величина, определяющая отношение приращения радиуса-вектора к промежутку времени ∆t.

Модуль средней скорости

(4)

Мгновенная скорость – векторная величина, определяемая первой производной радиуса-вектора движущейся точки по времени.

. (5)

Вектор мгновенной скорости направлен по касательной к траектории в сторону движения.

Модуль мгновенной скорости : (6)

Длина пути, пройденного точкой за промежуток времени от t₁ до t₂ :

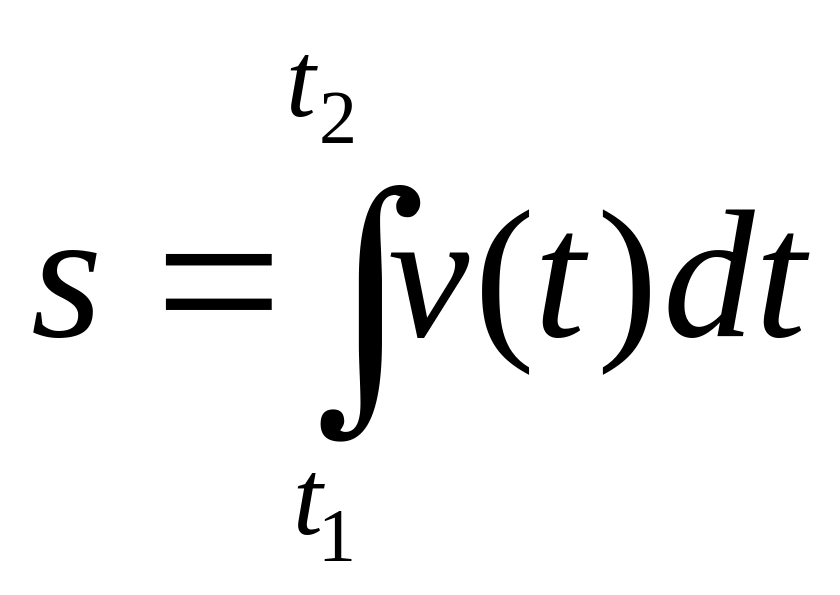(7)

При равномерном движении, когда величина скорости постоянна

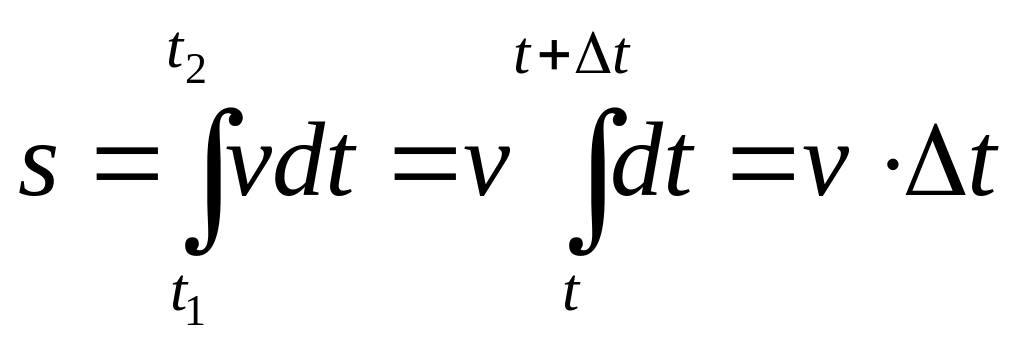(8)

Ускорение – характеристика быстроты изменения скорости по величине и направлению.

Среднее ускорение: . (9)

Мгновенное ускорение : (10)