4. Обработка результатов эксперимента

1. Погрешности при косвенных измерениях

1.1. Определение среднего значения

Если косвенно определяемая физическая величина X связана с измеряемыми величинами А, В, С, … известной функциональной зависимостью (расчетной формулой):

, (16)

то наилучшим значением величины Х будет Х_ср , которое вычисляют согласно приведенной выше формуле, подставляя в нее средние значения измеренных величин:

. (17)

1.2.2. Определение погрешности косвенных измерений

Погрешности измеряемых и табличных величин обуславливают погрешности Х_ср косвенно определяемой величины, причем наибольший вклад в Х_ср дают наименее точные величины, имеющие максимальную относительную погрешность . Поэтому, для повышения точности косвенных измерений, необходимо добиваться равноточности прямых измерений

(_А, _В, _С, … ).

Правила нахождения погрешностей косвенных измерений:

1. Находят натуральный логарифм от заданной функции

ln{X = f(A,B,C,…)};

2. Находят полный дифференциал (по всем переменным) от найденного натурального логарифма заданной функции;

3. Заменяют знак дифференциала d на знак абсолютной погрешности ;

4. Заменяют все «минусы», стоящими перед абсолютными погрешностями А, В, С, … на «плюсы».

В результате получается формула наибольшей относительной погрешности _x косвенно измеренной величины Х:

_x = =  (A_ср, B_ср, C_ср, …, A_ср, B_ср, C_ср, …). (18)

По найденной относительной погрешности _x определяют абсолютную погрешность косвенного измерения:

Х_ср = _x ^. Х_ср . (19)

Результат косвенных измерений записывают в стандартном виде и изображают на числовой оси:

X = (X_ср  Х_ср), ед.изм. (20)

Рис. 2.2.

Пример:

Найти значения относительной и средней погрешностей физической величины L, определяемой косвенно по формуле:

, (21)

где π, g, t, k, α, β – величины, значения которых измерены или взяты из справочных таблиц и занесены в таблицу результатов измерений и табличных данных (подобную табл.1).

1. Вычисляют среднее значение L_ср, подставляя в (21) средние значения из таблицы – π_ср , g_ср , t_ср , k_ср , α_ср , β_ср .

2. Определяют наибольшую относительную погрешность δ_L :

1. Логарифмируют формулу (21):

(22)

2. Дифференцируют полученное выражение (22):

(23)

3. Заменяют знак дифференциала d на Δ, а «минусы» перед абсолютными погрешностями – на «плюсы», и получают выражение для наибольшей относительной погрешности δ_L :

δ_L =

4. Подставляя в полученное выражение средние значения входящих величин и их погрешностей из таблицы результатов измерений, вычисляют δ_L .

3. Затем вычисляют абсолютную погрешность ΔL_ср:

Результат записывают в стандартном виде и изображают графически на оси L:

, ед. изм.

2. Правила округления результатов вычисления

Результаты математических действий над приближенными числами округляют до следующего количества значащих цифр:

1. при сложении и вычитании отбрасывают значащие цифры из последних разрядов, если их нет в одном их слагаемых;

2. при умножении и делении сохраняют столько значащих цифр, сколько их в приближенном числе с наименьшим количеством этих цифр;

3. при вычислении значений функций Aⁿ, 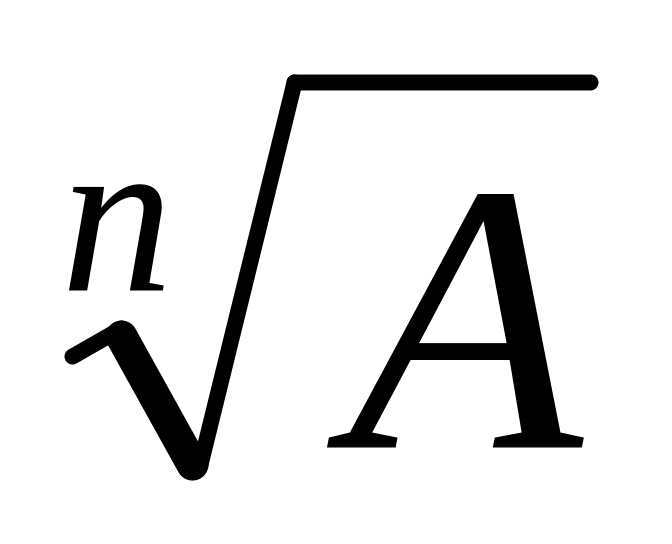, lgA оставляют столько значащих цифр, сколько их в А.

В промежуточных результатах сохраняют на одну («запасную») цифру больше.

Примеры:

1. 0,374 + 13,1 + 2,065 ≈ 15,5

Отброшены сотые и тысячные доли единиц, отсутствующие в числе 13,1.

2. 

Оставлены две значащие цифры по их количеству в числе 7,2.

3. 216³ ≈ 101·10⁵

Оставлены три значащие цифры по их количеству в числе 216.