5. Определение параметров функциональных зависимостей

Если изучаемые величины связаны функциональной зависимостью , то в табл.1 вводят столбцы для аргумента и функции . Строка «среднее» не заполняется, а погрешность определяется для одного (любого) опыта.

Например, если изучаемые в эксперименте величины и связаны функциональной зависимостью вида или , то обычно целью эксперимента является установление коэффициентов a и b.

Наиболее просто и достаточно точно можно получить искомые параметры, исследуя графики соответствующих зависимостей.

Логарифмируя выражение , получим:

, откуда .

Логарифмируя выражение , получим:

, откуда , потенцируя получают b.

Кроме графической аппроксимации возможно применение метода численного сглаживания экспериментальных зависимостей (метод наименьших квадратов)

6. Метод наименьших квадратов

Под методом наименьших квадратов понимается определение неизвестных параметров a, b, c,… принятой функциональной зависимости

y = f(x,a,b,c,…),

которые обеспечивали бы минимум среднего квадрата (дисперсии) ошибки

, (24)

где x_i, y_i – совокупность пар чисел, полученных из эксперимента.

Так как условием экстремума функции нескольких переменных является условие равенства нулю ее частных производных, то параметры a, b, c,… определяются из системы уравнений:

; ; ; … (25)

Необходимо помнить, что метод наименьших квадратов применяется для подбора параметров после того, как вид функции y = f(x) определен.

Если из теоретических соображений нельзя сделать никаких выводов о том, какой должна быть эмпирическая формула, то приходится руководствоваться наглядными представлениями, прежде всего графическим изображением наблюденных данных.

На практике чаще всего ограничиваются следующими видами функций:

1. линейная ;

2. квадратичная ;

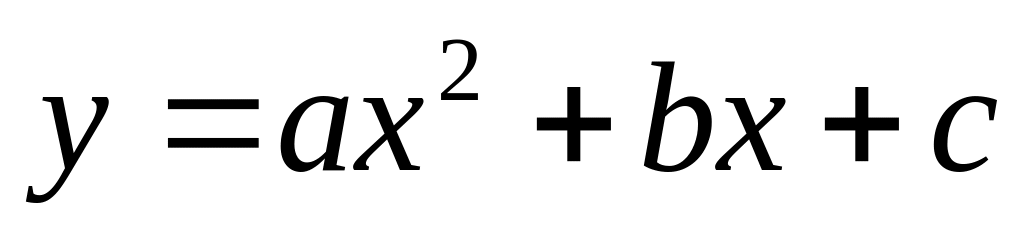3. гипербола ;

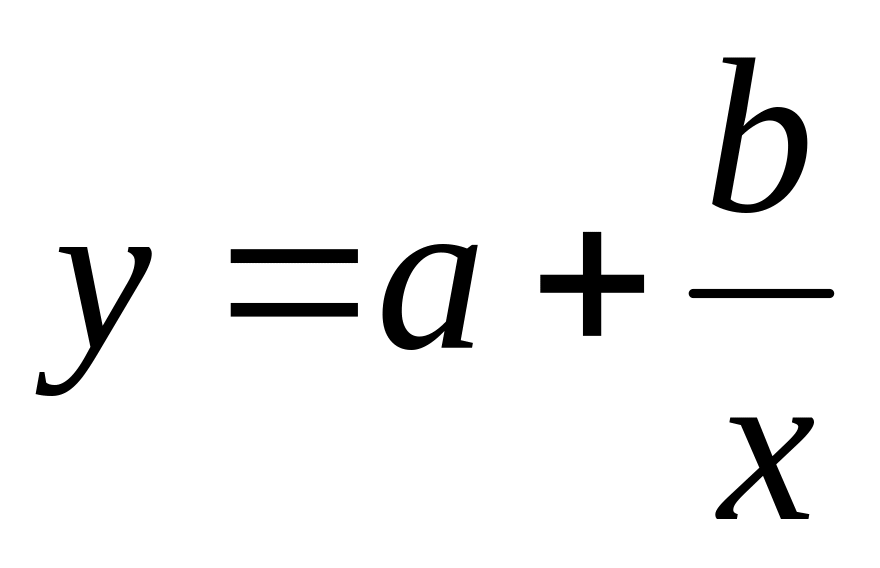4. показательная .

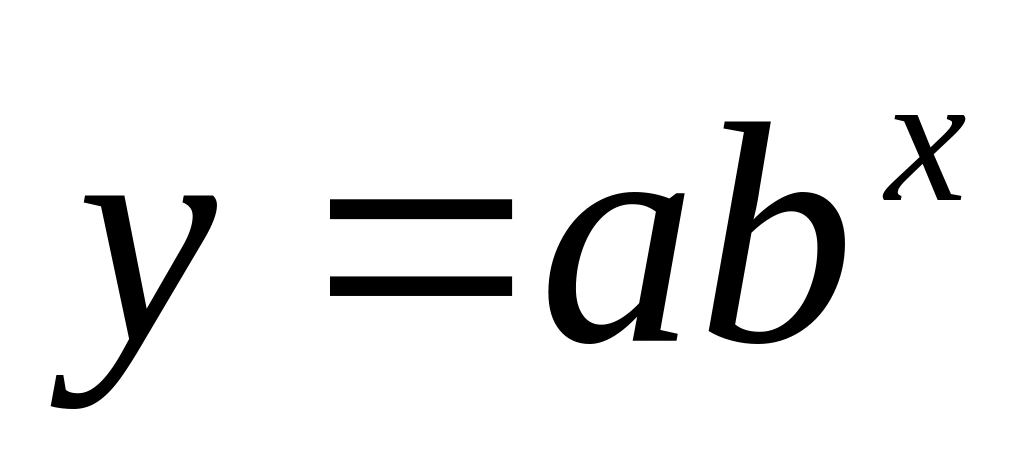Пример: Требуется определить вид и параметры функциональной зависимости двух переменных, заданных таблицей их значений:

		…		…
		…		…

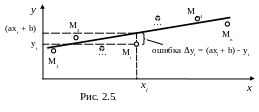
По данным таблицы строится график (Рис. 2.5)

Соответствующие точки на графике располагаются вблизи прямой линии. В этом случае лучше всего подойдет линейная функция вида . Коэффициенты a и b нужно подбирать так, чтобы сумма S квадратов отклонений вычисленных значений от наблюдаемых значений y_i принимала наименьшее значение (26):

Сумма (26) является функцией двух переменных a и b, поэтому она принимает минимальное значение при тех значениях a и b, при которых обращаются в нуль частные производные этой функции по каждой переменной:

и . (27)

Находим частные производные:

(28)

;

.

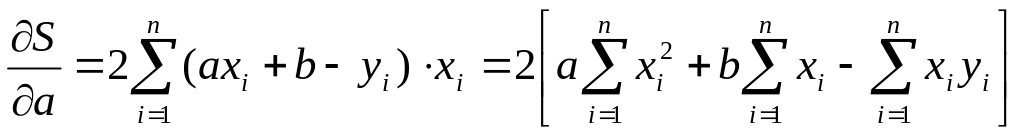
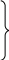
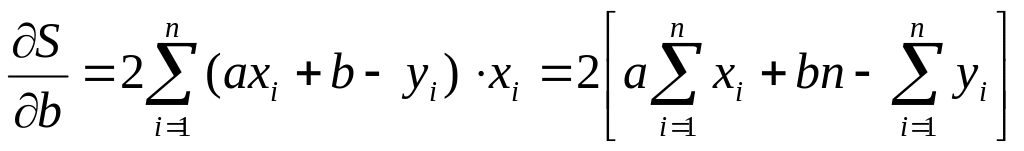Приравнивая каждую частную производную в нулю, получаем систему двух линейных уравнений относительно a и b:

(29)

Подставляя найденные значения параметров a и b в выражение выбранного нами вида аппроксимирующей табличные данные функции , получаем вместо набора дискретных значений, полученных экспериментальным путем, вполне определенную функциональную зависимость .

_________ Конец 1 лекции ___________